指令选择的调查
摘要
指令选择是代码生成中三个主要的优化问题之一 – 其它两个是指令调度和寄存器分配。指令选择器的任务是将来自目标独立表示的输入程序转换为一个特定目标的形式,期间会充分利用可以使用的机器指令。因此,指令选择是生成在特定目标机器上既正确又高效运行的代码至关重要的一部分。
尽管自 1960 年代后期以来一直在研究,但是这个领域的上一篇综合调查是写于 30 多年前的了。因为,自从它发表之后出现了许多新的方法和技术,所以需要对当前的文献进行新的审查。这个报告解决了这个需求,给出了一个广泛的调查,以及指令选者过时的方法和最新方法的分类。因此,这个报告取代和扩展了之前的调查,并且尝试着指出未来的研究方向。
简介
任何软件的每部分实现承诺 – C 写的基于 GUI 的 Windows 应用,数学计算的高性能 FORTRAN 程序,或者 Java 写的智能手机 app – 都需要一种或者另一种形式的编译器。它的核心目的是转换一个输入程序的源代码 – 相关高级编程语言写的 – 到一个等价的低级程序代码表示,其对应于特定的目标机器。程序代码转变为机器代码 – 与编译相比是一个相对容易的任务 – 然后可以在指定的目标机器上执行。最后,编译器一直是,并且很可能永远是利用现代技术的重用推动者。因此,自 1940 年代第一台计算机开始出现以来,一直在积极研究中,编译是计算机科学中最古老和研究最多的领域之一。
为了达成这个任务,编译器需要处理范围广泛的中间问题。其中一些问题包括语法分析,转变为中间表示,目标独立优化,以及代码生成。代码生成是生成目标机器相关的程序代码的过程,依次由三个子问题组成 – 指令选择,指令调度,以及寄存器分配 – 本报告关注第一个问题。
之前的一些在某种程度上讨论指令选择的调查是由 Cattell[45],Ganapathi 等[116],Leupers[169],以及 Boulytchev 和 Lomov[33] 产生的。但是,最后一篇广泛的调查 – Ganapathi 等的 – 是 30 年前发布的。而且,经典的编译器书只是简短的讨论指令选择,因此提供的见解比较少;在构成编译器书的 4600 多页综合正文中[8,15,59,96,173,190,262],少于 160 页 – 其中有很大的重叠,且基本上只讨论树覆盖 – 用在指令选择上。因此,需要对该领域进行新的,实时的研究。这个报告解决了这个需要,通过描述和回顾了已经存在的方法 – 包括过去和现在的 – 指令选择,因此取代和扩展了之前的调查。
这篇报告的结构如下。本章剩余部分介绍和描述了指令选择的任务,比较了已经存在的方法解释了通用的问题,且简要介绍了有关代码生成的第一篇论文。然后第 2 章到第 5 章,分别讨论了指令选择的基本原则:第 2 章介绍了宏展开;第 3 章讨论了树覆盖;其在第 4 章和第 5 章扩展到了 DAG 和图覆盖。最后,第 6 章给出了一个结论结束这个报告,其中我尝试识别出未来研究的方向。
这篇报告也包含了几个附录。附录 A 给出了一张表总结了本报告中涵盖的所有方法,附录 B 中有一张图标说明了文章出版的时间线。为了一些必要的背景信息,附录 C 提供了一些图的正式定义。附录 D 中包含了一些术语和概念的分类,用于整个报告,促进讨论且避免混淆。最后,附录 E 中提供了本文档的修订日志。
什么是指令选择 ?
如本章一开始声明的,编译器的核心目的是将高级别源码写的程序转换成低级别机器码,其是将要执行程序的特定硬件平台特有的。这个源码可以用一些编程语言表达(如,C,Java,Haskell 等),然后硬件通常是一个特定模型的处理器。后面正在编译的程序称为输入程序,然后它被编译的硬件称为目标机器(这些定义在附录 D 中也可以找到)。
编译器内部
为了给指令选择一个上下文,让我们简要地检查下编译器做了哪些事情。图 1.1 给出了大部分编译器的基础设施。首先是前端解析,验证,然后转换输入程序的源码到一个等价形式即中间表示,或者简写为 IR。IR 代码是编译器内部使用的格式,它还将编译器的其余部分于特定编程语言的特征隔离开来。因此,通过简单地为每个语言提供一个前端,就可以在相同的编译器中支持多个编程语言。
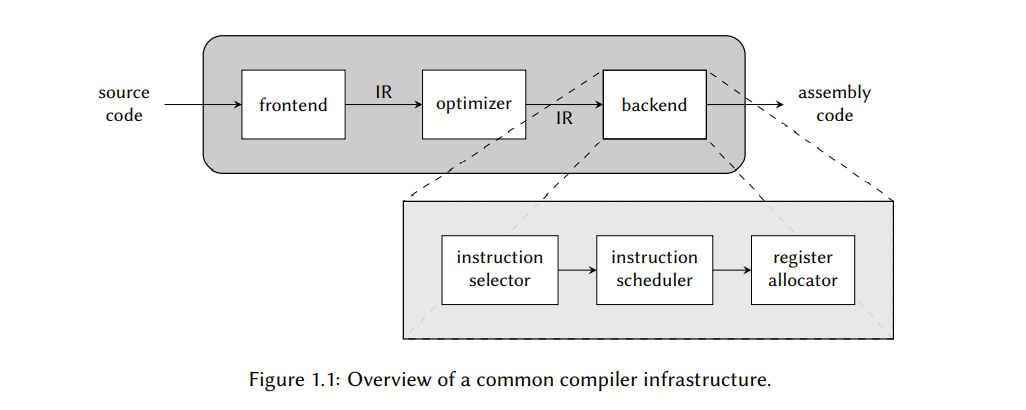
执行一系列目标机器无关的优化之后 – 如,死代码消除和评估带有常量的表达式(被称为常量折叠) – IR 代码被代码生成器后端转换为一组机器相关的指令,称为汇编代码;这是允许输入程序在特定目标机器上可以执行的部分。为了做这个,我们需要决定哪个目标机器的机器指令可以用于实现 IR 代码;这是指令选择器的职责。对于已选择的指令,我们也需要决定它们出现在汇编代码中的顺序,这是指令调度器关心的事。最后,我们必须决定如何使用目标机器上可用的有限寄存器集,通过寄存器分配器来管理。最后两个任务超出了本报告的范围,不会在进一步详细地讨论了。
指令选择器主要是要选出可以实现与输入程序相同期望行为的机器指令,然后次要目标是,要产生高效的汇编代码。我们将其重新表述为下面的子问题:
- 模式匹配 – 检查何时何地可以使用的某条指令;然后
- 模式选择 – 当多个选项存在的时候,决定当前场景中可以选择的指令。
第一个子问题与寻找机器指令候选有关,而第二个子问题与从这些候选指令选出一个子集有关。有些方案将两个子问题合并到了一步,但大部分都是保持两者分开的,主要区别是他们如何解决模式选择的问题。通常后者被表述为一个优化问题,其中每条机器指令都被赋予了一个开销,目标是最小化已选择的指令的总开销。根据优化准则,成本通常是反映目标机器执行给定机器指令所需的周期数。
目标机器的接口
指令选择期间可以使用的有效机器指令集是由目标机器指令集架构(ISA)决定的。大部分的 ISAs 提供了丰富且多样的指令集,它们的复杂范围从执行简单只有一个操作的简单指令 – 如,算术加法,到高复杂的指令–如,拷贝一个内存位置的内容到另一个位置,增加一个地址指针,以及重复直到遇到某个停止值。因为指令集很少是正交的,一个特殊的操作集总是存在超过多种实现方式。例如,表达式$a + (b \times c)$ 的计算,可以通过首先执行一个 mul 指令 – 其实现了 $d\leftarrow b\times c$ – 然后紧跟着一条 add 指令实现了$e\leftarrow a + d$来计算;或者它可以通过执行一条单一的 mulacc 指令来计算,它实现了 $a \leftarrow a + (b \times c)$。
根据目标机器的特性,在执行特定任务时,一些指令序列比其的更高效。对于数字信号处理器(DSPs)更是如此,其为了提高某个算法的性能,给出了许多的客制化机器指令。根据 1994 年的研究[254],从 C 程序到目标为 DSPs 的编译器生成的汇编代码的时钟周期固有开销是手写汇编代码的 1000% 多,因为编译器未能充分利用目标机器的能力。最后,生成的机器代码的质量高度依赖于编译器利用硬件相关的特性和资源的能力,其中指令选择器是达成这一目标的关键(但是不是唯一的)组件。
编译不同方法的问题
如同我们在前一节看到的,ISA 由许多不同类型的机器指令组成。 但是,当前所有指令选择方法的共同特定是,没有一个可以处理 ISA 中的每一条有效指令的。最终,大多数提出新指令选择技术的论文讨论的指令集都有所不同。例如,早期文献中,“复杂机器指令”是指使用不同复杂度的方案计算内存地址的内存加载和存储指令。这些方案称为地址模式,使用合适的地址模式可以降低代码大小,同时提高性能。举个例子,让我们假设我们需要从一个 驻留在内存的1-字节数据的数组中的特定位置加载一个值。因此,我们想要的值的内存地址是 @A + offset,其中 @A 指的是第一个元素的内存地址,通常叫基址地址。一个合理获取这个值的方法是首先执行一个 add 指令来计算 @A + offset 到一些寄存器 $r_x$ ,然后执行一条 load 指令其从 $r_x$ 中获取内存地址。这样的 load 指令被认为是有绝对或直接地址模式。但是,如果ISA 提供了一条带有索引地址模式的 load 指令 – 其地址获取的地方是基础值加上偏移 – 这样我们就可以远离只使用一条机器指令了。相比之下,在现代指令选择方法中高效处理这样的地址模式是微不足道的,更复杂的机器指令通常是产生多个值的,或者是只能在特定场景下使用的(或不能使用的)。
为了解决这个问题,使得我们可以比较指令选择的不同方案,我们将会引入定义一组属性,每个都与某类机器指令相关。
机器指令属性
单输出指令
最简单的机器指令种类是一组单输出的指令。这些只产生单个可见的输出,“可见”的意思是一个值可以被程序读和访问。这包含了所有实现单操作数的指令(如,加法,乘法,和位操作如 OR 或者 NOT),也包含了许多复杂的指令,其实现了几个操作数如刚才讨论的带有复杂地址模式的内存操作(如,将基址寄存器 $r_x$ 加上偏移标识的寄存器 $r_y$ 加上一个立即数得到的内存位置里的值加载到寄存器$r_d$);只要可观察的输出值可以构成单一值,一个单输出指令就可以是任意复杂的。
多输出指令
如预期的,多输出指令从一个相同的输入产生了多个可观察的输出值。一个包含 divrem 指令的例子,它计算了两个输入的商和余数,算术指令也一样,除了计算结果,也设置状态标志。一个状态标志(也称为条件标志或者条件码)是每一位都表示结果的一个额外信息,如,一个进位溢出或结果是 0。因为这个原因,这样的指令总是被说是有副作用的,但是实际上这些位只不过是指令额外产生的信息,因此被认为是多输出的指令。加载和存储指令会访问内存中的值,然后增加地址指针的值,也会被认为是多输出指令。
不相交输出指令
从许多不同输入值产生多个可观察值的机器指令被认为是不相交输出指令。它们类似于多输出的指令,除了后者所有的输出值都是来自于相同输入值的。另一种形式说则是如果每个相关的输出形成表达式地图,所有的这些图都是相互不相交的;我们会在下一章解释这个图是如何形成的。不相交指令典型的包含 SIMD(单指令,多数据)和向量指令,其同时在许多不同的输入值上执行相同的操作。
内部循环指令
内部循环指令表示行为是执行一些内部循环的机器指令。例如,TI TMS320C55x [247] 处理器提供了一条 RPT k 指令,重复执行后面的指令 k 次,k 是立即数作为机器指令的一部分给出。这些指令是最难利用的指令之一,今天要利用它们要么通过客制化优化路径,要么通过编译器特殊的支持。
相互依赖的指令
最后一类是相互依赖的指令。这是指那些携带额外限制的指令,这些限制会在指令以特定的方式组合的时候出现。一个包含 ADD 指令的例子,这条指令来自 TMS320C55x 指令集,如果 ADD 使用特定的寻址模式,则它不能与 RPT k 指令组合在一起。如同我们将在这个报告里看到的,这是另一类大多数指令选择器都难以处理的机器指令,因为它们通常不满足基础技术所作的一组假设。此外,它们只在某些场景下出现。
最优指令选择
当使用最佳指令选择这个术语时,大部分文献都假设 – 通常是隐式的 – 有如下的定义:
定义. *一个指令选择器,能够以开销 $c_i$ 建模一组机器指令 I,是最优的,只要对任意给定输入程序 P,它选出了一个集合$S\subseteq I$ s.t. S 实现了 P,且不存在其它的集合 $S’$ 也实现了 P,其中 $\sum_{s’\in S^{‘C}s’} < \sum_{s\in S^Cs}$*。
换句话说,通过这个指令选择器处理和利用相同的机器指令,无法实现更低成本的汇编代码,则认为这个指令选择器是最优的。
这个定义有两个缺陷。首先,“可以被建模的机器指令”的条文限制了最优性的讨论,即指令选择器是否已经极致地利用了指令的讨论限制在它能处理的指令集上。其它的,不支持的机器指令,就算能产生更高效的汇编,也被简单的忽略了。尽管这个定义使得支持相同机器指令的指令选择器可以相互比较,但是它也允许将处理不同指令集的两个指令选择器识别成都是最优的,即使其中一个比另一个明显能产生更高效的代码。忽略违规条文可以移除这个问题,但也会使得现有的所有指令选择技术都变成是次优的。除了最简单的 ISAs,对于特定的输入程序,似乎总是存在一些机器指令可以提高代码质量,但是不能被指令选择器处理。
更要紧的是另一个问题,两个可比较的指令选择器可能会选择不同的指令,从指令选择的角度来看两个都可以被认为是最优的,却最终产生指令不成比例的汇编代码。例如,其中一组指令可能会使得后续的指令调度和寄存器分配能更好的运行,而另一组则不行。这强调了代码生成的一个众所周知的特性:指令选择,指令调和寄存器分配是相互关联在一起,形成一个复杂系统,来影响最终编译后的汇编代码的质量,且经常出现的是反直觉的方式。因此,为了产生真正最优的代码,三项任务需要协同解决。有许多的研究已经开始设计这样的系统了(有些本报告覆盖到了)。
因此,将最优指令选择作为一个孤立概念的想法是徒劳的,然后如果一个指令选择方法宣称是“最优的”,则明智的做法是密切关注它支持的机器指令集。不幸地是,这个概念已经在编译器社区中牢牢地确立了,并且渗透到文献中了。由于这个原因 – 且没有更好的选择 – 我将在本报告中遵守这个定义,但尽量少使用它。
指令选择的史前史
代码生成的早期论文是从 1960 年代早期开始出现的 [13,99,193,214],它们主要关注基于累加寄存器的目标机器上如何计算算术表达式。对于一条指令而言,一个累加寄存器是可以同时作为输入值和目的的寄存器的(如,$a \leftarrow a + b$),在早期的机器中很流行,因为它可以用比较少的寄存器来构建处理器。虽然这个简化了硬件制造过程,但是,不容易自动生成表达式的累加寄存器和内存间的最小传输数量的汇编代码。
在 1970 年代,Sethi 和 Ullman [228] 将这些想法扩展到了带有 n 个通用寄存器的目标机器上,然后给出了一个评估带有通用子表达式的算术语句的算法,可以生成尽可能少语句的代码。后来,Aho 和 Johnson[3] 扩展了这个工作,应用动态规划开发了一个代码生成的算法,可以处理带有类似间接地址等更复杂地址模式的目标机器。本报告后面将会在重新给出这个方法,因为后续许多指令选择的方法都受到这个技术的影响。
这些早期技术的共同点是指令选择的问题被有效的忽略和规避。例如,Sethi 和 Ullman 以及 Aho 和 Johnson 的方法都假设了目标机器具有简洁的数学性质,没有任何的奇异机器指令和多个寄存器分类。由于没有或者很少有机器具有这样的特性,所有这些算法在实际设置中都无法直接应用。
由于缺乏正式的方法,第一个指令选择器通常都是手工写的,基于临时的算法完成的。这意味着高效和可移植性之间的权衡:如果指令选择器太通用,则生成的汇编代码可能无法执行;如果它过于紧密地针对特定目标机器量身定制,则会限制编译器支持其它的目标机器。因此,移植这样的指令选择器涉及到手工修改和基础算法的重写。对于特殊的机器,带有多有个寄存器类且需要不同的指令来访问不同的类,原始的指令选择器甚至可能根本不能用。
但即使指令选择器是要以有助于编译器移植的方式来构建,也不是很清楚如何实现这一目标。下一章中,我们将研究解决这个问题的第一种方法。
宏展开
第一篇介绍将指令选择作为一个独立问题来处理的方法的论文出现在 1960 年代后期。在这些设计中,指令选择通过在由输入程序组成的代码上进行模板匹配来驱动。命中后,使用匹配的程序字符串作为参数,执行相对应的宏。每种语言结构,共同构成了表达输入程序的编程语言,通常都有自己的宏定义,可以输出目标机器合适的汇编代码。多个语言构造也可以合并成单个模板,从而更好地利用指令集。对于一个给定的输入程序,对于一个给定的输入程序,指令选择器将会以遍历输入程序的程序方式运行,将代码与模板匹配,然后执行匹配后的宏。如果一些文本无法匹配到任何的模板,则指令选择会失败,然后报告一个错误,表明它无法为特定的输入程序,产生特定的目标机器上的有效汇编代码(这种情况最好不要发生)。
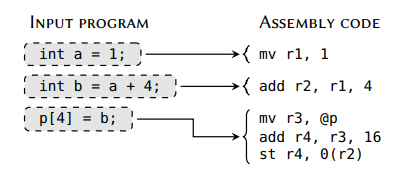
因此,模板匹配的过程对应与前一章描述的模式匹配问题,在多个匹配宏间选择的过程对应于模式选择的问题。但是,据我所知,所有的宏展开的指令选择器都是立即选择首先匹配到的宏,从而使得后一个问题变得轻而易举。
通过保持这些宏的实现与核心实现的分离 – 核心指的是指令选择中模板匹配和宏执行的部分 - 减少了将编译器移植到不同目标机器的工作量,较早的时候,整体的方式经常要重写整个代码生成器的后端。
朴素的宏展开
早期的方法
我们将直接应用刚描述过的原理的指令选择器称为朴素宏展开 – 主要是因为下面的原因。首先,这种实现的宏要么手写 – 如 Ammann 等人 [11,12] 开发的 PASCAL 编译器,或者通过机器相关的描述文件自动生成。这种文件通常使用专用的语言描述,这些年出现了许多这样的语言和工具(有些也消失了)。
其中一个例子是 SIMCMP,一个由 Orgass 和 Waite [200] 开发的宏处理器,它被设计成有利于自举的形式。SIMCMP一行一行地读取它的输入,与可用的宏模板逐行比较,然后执行第一个匹配上的宏。图2.1给出了此类宏的一个例子。

另一个例子是GCL(Generate Coding Language),它是Elson和Rake[78]开发的语言,用于PL/1编译器从抽象语法树(ASTs)生成机器代码。一个AST是一个源码基于图的表示,它通常形似一个树形(附录C提供了图、树、节点、边和其它本文会遇到的相关术语的精确定义)。这些树最重要的一个特性是只有语义有效的输入程序会被转成AST,这简化了指令选择器的任务。但是,宏展开的基本原理是保持不变的。
使用中间表示替代语法树
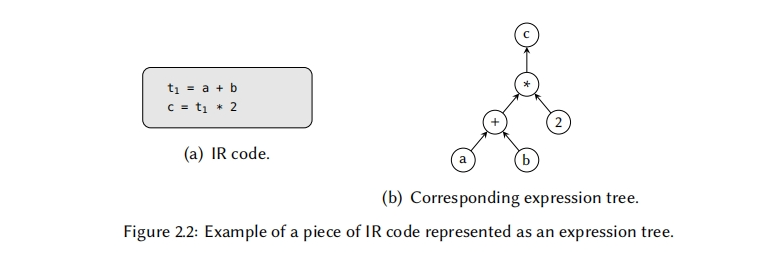
直接在源码上执行指令选择–在文本形式上或AST上–会造成编译器和特定变成语言紧耦合的缺陷。因此,大部分编译器基础设施依赖于一些机器无关的中间表示(IR),它将一系列优化及后端与编程语言的细节隔离开。和AST一样,IR代码经常被表示成图称为表达式图(或者表达式树,取决于它的形状),其中每个节点表示一个特定操作,每条直接边表示两个操作之间的一个数据依赖。图2.2给出了一个表达式树的例子;在这个报告里,我们都会将树的根节点画在顶部,但是要注意的是其它论文可能会跟这个约定不同。通常也会忽略中间变量,只保留表示表达式输入输出的值。
最早基于IR的方案中的一个是Wilcox[261]开发的。它实现在PL/C编译器中,AST首先被转换为机器无关汇编代码形式,由SLM(Source Language Machine)指令组成。然后指令选择器使用ICL(Interpretive Coding Language)(见图2.3)语言定义的宏将每条SLM映射成一到多条架构相关的机器指令。
实际中,这些宏被证明是繁杂的:宏中有许多的细节,如地址模式和数据位置,不得不人工地处理;在ICL的场景中,宏作者还不得不记录哪些是属于最终的汇编代码,哪些变量是辅助的只用于帮助代码生成过程。Young[269]提出了一个简化这个任务的设想–但从没有被实现–一个面向实现细节抽象出来的称为TEL(TEmplate Language)的高级语言;这个想法首先使用TEL表达宏,然后根据规范自动生成更低级别的ICL宏。

根据机器描述自动生成宏
和Wilcox的方式一样,许多早期的宏展开指令选择都依赖于复杂难以编写的宏,并且编译器开发者总是将寄存器分配纳入到宏里考虑只会加剧这个问题。例如,如果目标架构机器存在多类寄存器类型–有特殊的机器指令将数据从一类寄存器拷贝到另一类寄存器–需要有一个记录描述程序值存储的寄存器。然后,根据寄存器分配的情况,指令选择器可能需要输出适当的数据传输指令到构成输入程序的汇编代码中。由于需要处理的情况是指数级的,故宏设计者需要管理的复杂度也是极大的。
通过状态机处理数据传输
第一个尝试解决这个问题的方案是Miller[189]在1971年做的,他开发了一个称为DMACS(Descriptive MACro System)的代码生成系统,这个系统可以自动地在内存和不同的寄存器类型之间自动推导出必要的数据传输。通过在一个分离的文件里提供这些信息,DMACS是第一个允许独立声明目标架构细节的系统,其它系统都是嵌入到宏里面隐式定义的。
DMACS依赖于两个专有的语言:MIML(Machine-Independent Macro Language),它声明了一组程序式两参数命令,作为IR格式(见图2.4的例子);一个声明式语言OMML(Object Machine Macro Language)用于实现将每个MIML命令转为汇编代码的宏。因此,这个方案类似于Wilcox应用的那个。
首先,在为一个新目标机器添加支持的时候,宏设计者指定了一组可用的寄存器类型和它们之间可用的转换路径(包括内存)。然后,对于每个OMML宏,设计者通过提供一组实现相应的目标架构上的MIML命令的机器指令定义它们。如果需要,可以给出一组机器指令仿真MIML命令的效果。对于每个机器指令,添加一些约束强制输入和输出数据出现在机器指令的特定位置上。图2.5给出了IBM-360机器的一个简短的OMML定义。
DMACS使用这些信息来生成一个状态机集合,其中每个状态机确定了一组给定输入值是如何被转换成给定OMML宏上允许的位置的。一个状态机由一张有向无环图组成,其中每个节点表示寄存器类型和内存的一个特定配置,它们中有一些被标记成许可的。边表示一个状态是如何被转成另一个的,并被一条机器指令标记着,当在特定输入值上执行时,它会使能一个转换。在编译的时候,指令选择器会根据特定的状态机遍历每个MIML命令,期间通过使用前一个的输入值来初始化状态机,然后输出每条被拿到的边上的机器指令,直到状态机达到允许的状态。


Miller 的工作是具有开拓性的,但也存在一些局限性:DMACS只能处理由整型值和浮点值组成的算术表达式,只支持有限的地址模式,并且无法建模其它诸如基于栈的架构。后来Donegan[72]扩展了这些想法,提出了一个称为CGPL(Code Generator Preprocessor Language)的新编译器生成语言,但是这个设计一直都是在论文层面从没有被实现过。Tirrell[242]和Simoneaux[232]已经开发了一个相似的方案,还有Ganapathi等人[116]在他们的调查文章中描述了另一个基于状态机的编译器称为UGEN,源自于U-CODE[204]。
进一步提升
在1975年,Synder[233]在第一个完全可操作和可移植的C编译器上进行实现,它的架构相关的部分可以完全通过一个机器相关的描述进行自动生成。这个方法与Miller的方法相似,其中前端首先将输入程序转换成一个抽象机器的等价表示,由AMOPs(Abstract Machine OPerations)组成,然后通过宏将它们展开成机器指令。和Miller的类似,抽象机器和宏是由机器描述语言指定的,但是它可以处理更复杂的数据类型,地址模式,对齐,以及跳转和函数调用。如果有需要,更复杂的宏可以被定义为客制化C函数。我们主要提及的是Snyder的工作,因为它后来被Johnson[143]在PCC的实现中采用了,我们在下一章会讨论它。
Fraser[106, 107]也认识到需要人类知识来指导代码生成过程,并实现了一个系统便于在需要的时候田间手写规则。首先,输入程序被转换成一个基于XL的表示,它是一种高级汇编代码;例如,XL提供了数组访问的原语和for循环。就像Miller和Snyder,每个机器指令都有一个独立的描述,每个描述都对应一个不同的XL原语。如果输入程序的一些部分无法通过指令实现,则指令选择器会一直调用一组改写XL的规则直到找到方案。例如,数组访问被分解为更简单的原语。此外,可以使用相同的规则库来提高生成的汇编代码的代码质量。因为这些规则都是通过分离的文件提供的,所以它们可以根据需要进行定制和增强,以适应特定的目标机器。
正如我们将看到的,这种“按摩”输入程序直到找到解决方案的思路已经被许多指令选择方法以一种或者另一种形式采用了,这些方法既有早于Fraser方法,也有晚于他的。然而,在大多数情况下,有一个共同的缺陷是,如果特定目标机器的规则集不完整 – 要确定是否处于这种情况是很困难的 – 指令选择器会陷入无限循环的困境中。此外,这些规则通常无法被其它目标机器重利用。
使用表格进行更高效的编译
尽管它已经很简单了,但通过将1对1或1对多映射表示为一组表,宏展开指令选择器可以更简单。这进一步强调了指令选择器的机器无关核与机器相关映射的分离,并且允许更密集的实现,更少的内存和更少的编译时间。
将机器指令表示为编码框架
在1969年,Lowry和Medlock[180]是较早之一提出用于代码生成的表驱动方法。在他们的FORTRAN H 编译器的实现中,Lowry和Medlock在每条机器指令上使用了编码框架,它们由比特位串组成。这些比特位代表了机器指令允许的模式等限制 – 如从内存加载,从寄存器加载,操作但不存储,使用它或者基础寄存器等 – 针对操作数和结果的。然后这些编码框架与输入程序对应的位串进行匹配,编码框架里出现的“X”表示一个任意匹配符。
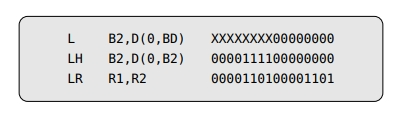
但是,Lowry和Medlock编译器中的表只能用于最基本的机器指令,并且只能手写。后来Tirrell[242]和Donegan【72】开发了更通用的方法,但他们也存在相似的缺陷,即对目标架构做了过多的假设,这阻碍了编译器的可重用性。
自顶向下宏展开
后来Krumme和Ackley【164】提出了一种异于之前方法的表驱动设计,它详细地枚举了给定表达式树的可选择指令,调度和寄存器分配所有可用的组合情况。它被实现在目标是DEC-10机器的C编译器里,允许将代码大小作为一个优化目标,这在当时还不是一个常见的特性。Krumme和Ackley的后端应用了一个递归算法,它从表达式树的根节点开始选择指令,然后一路向下。与之相对应的是,自底向上的技术,我们会检查完所有的叶子节点,在向上遍历。这两个技术我们暂时只介绍到这里,因为我们在下一章中会在重新深入地自底向上和自顶向下的指令选择技术。
不用多说的是,在代码生成中枚举所有可用的组合会导致组合爆炸,因此实际上是无法生成和检查所有组合的。为了抑制巨大的搜索空间,Krumme和Ackley使用了分支定界的搜索策略。分支定界里的思路是比较简单的:在搜索过程中,总是记住当前最好的结果,然后裁剪掉搜索树上所有被证明是不好的结果。但是剩下的问题是,如何证明搜索树的一个给定分支确实会导致结果会比我们当前获得的结果更糟糕(因此才可以被丢弃)。Krumme和Ackley只是部分解决了这个问题,仅修剪了那些最终一定会导致失败的分支(如没有任何结果的)。细节就不在展开,它不是通过一个机器指令表而是通过多个表完成的–一个模式一个表。在这种情况下,模式以表达式的结果为导向,例如,它是存储在寄存器还是内存中。通过为每个模式提供一个表格–以分层形式构建的–指令选择器可以往前看,然后识别当前已经选择的机器指令是否可以导致结束。
但是,以此作为分支定界的唯一方法,指令选择器会在搜索空间中做许多不必要的重复访问,因此,这个方法无法扩展到更大的表达式树上。
落后
尽管有上述改进,宏展开指令选择器的主要缺陷还存在,即它一次只能处理一个单AST或IR节点展开的宏,因此被限制在只能支持单输出机器指令。由于这会对表现出更复杂功能的目标机器的代码质量产生不利影响,如多输出指令,因此仅基于朴素宏展开的指令选择器被更新的,更强的技术快速地替换掉了–其中一个本章后续会讨论到–它们是从1970年代后期开始出现的。
在第一代动态代码生成系统中被重新应用
不在常见之后,朴素宏展开指令选择器后来又在1980年代和1990年代开发的第一代动态代码生成系统中被简短地重现了。在这种系统里,输入程序首先被编译成字节码,这是一种架构无关的机器码,可以被底层运行环境解析。通过在每个目标机器提供一个完全相同的环境,相同的字节码不需要在重新编译就可以在多个系统中执行。
但是,以解释模式运行程序通常比以本地机器代码的方式执行程序要慢很多。通过在运行环境中集成一个编译器,可以降低性能损失。与执行过程并行的是,字节码可以采集性能数据和频繁执行的代码段,如内层循环,然后在运行中编译成本地机器码。这个概念被称为及时编译 – 或者简称为JITing – 它在提高性能的同时也保留了字节码的可移植性。如果,运行字节码和可替代的本地机器码的性能差异非常大,则编译器可以承担的起产生低质量汇编代码的开销,从而降低运行环境的高开销。这对于最早的动态运行环境是非常重要的,因为那时候硬件资源还很稀缺,这使得宏扩展指令选择成为一个合理的选择。SMALLTALK-80【68】,OMNIWARE【1】(JAVA的前身),VCODE【82】,和GBURG【103】等都是在小型虚拟机中使用的。
然而随着技术的进步,动态代码生成系统也开始转变到更强的指令选择技术,如我们下一章介绍的树覆盖。
通过窥孔优化提升代码质量
一个提升生成汇编代码质量的早期方法 –仍然还在使用– 是随后执行一个优化过程,它尝试将几条机器指令合并替换为更短的、更有效的备选方案。这个过程被称为窥孔优化,原因我们随后会介绍。
窥孔优化
在1965年McKeeman【188】提出使用一个简单但容易被忽视的优化方式,作为代码生成的后一个阶段,它检查汇编代码的一些小的指令序列,然后尝试将两条或者多条相邻指令合并成单条指令。同时期,Lowry和Medlock【180】也提出了相似的想法。通过这个优化,在压缩代码大小的同时也提高了性能,因为使用复杂机器指令通常比使用几个更简单指令实现相同功能要更高效。因为其观察窗口较窄,这个技术被称为窥孔优化。
使用寄存器转换表建模机器指令
由于这种优化是针对特定目标机器量身定制的,最早的实现是临时的手工完成的(并且现在也经常是这样子做的)。但是在1979年,Fraser【102】给出了第一个允许这种程序自动生成的方法。Davidson和Fraser【65】的长论文中也描述了它。
就像Miller,Frasery也开发了一个允许在符号机器规范里单独描述机器指令的语义的技术,它替代了需要要隐式嵌入这些信息到手写例程的技术。这个规范描述了每个机器指令对目标机器寄存器的可观察影响,Fraser称之为register transfers。因此,每条指令都有一个相关的寄存器转换模式或者寄存器转换表(RTL) – 后面我们使用后一个术语。例如,假设我们有一个三地址机器指令add,它执行一个算数加法,使用一个输入寄存器$r_s$和一个立即数imm,存储结果到寄存器$r_d$,并设置0标志z。则相关的RTL可以表示为
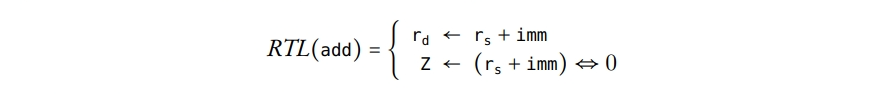
然后这个信息会给到一个称为PO(Peephole Optimizer)的程序,它产生一个优化例程,在已生成的汇编代码上做两遍。第一遍从后向前遍历汇编代码,判断汇编代码里每条机器指令的可观察效果(即,RTL)。它从后向前运行便于消除对程序可观察行为没有影响的作用:例如,如果后续没有指令读取条件标志的值,则它的值是不可观测的,因此可以被忽略。然后,第二遍检查两条相邻机器指令的合并后的RTLs是否等价与某些其它指令;在PO中,这些检查是通过一系列字符串比较完成的。如果可以找到这样的指令,则进行替换,然后进程回退一条指令,从而可以检查新指令和它在汇编代码中的下一条指令的合并性。这种方式下替换是可以级联的,因此多个机器指令可以被归约成一条等价的指令(假设每个中间步骤都存在适当的机器指令)。
PO的开拓性也存在一些局限性。主要的缺点是它只能处理两条指令的合并,并且这两条指令在汇编代码中必须是按解析序相邻的,不能跨过标签边界(即,属于分离的基本块;这些描述在124页的附录D中)。Davidson和Fraser【63】后来通过构建数据流图移除了解析序相邻的限制 – 与表达式图或多或少有些相似 – 在这个上面操作,替代了直接在汇编上的操作,同时也将指令窗口从2扩展到3。
进一步提升
有许多的研究投入到了提升窥孔优化的自动化方法中。在1983年Giegerich【119】提出了一个正式方案,消除了固定指令窗口的限制。随后,Kessler【155】提出了一个方法,RTL的合并和比较可以在编译器构建阶段就进行预计算,从而降低编译时间。后来Kessler【154】扩展了他的方法包含了n大小的指令窗口,类似于Giegerich的,但是是以指数级成本为代价的。
另一个方法是Massalin【187】开发的,他实现了一个被称为SUPEROPTIMIZER的系统,这个系统接受小的输入程序,以汇编形式编写的,然后详尽地组合机器指令序列以寻找更短的实现,同时保持和输入程序相同的行为。后来Granlund和Kenner【128】在最小化输入程序使用的分支数量的方法中采用了Massalin的想法。然而,没有一个方法在正确性上有保证,因此需要人工检查最终的结果。最近,Joshi等人【145,146】提出了一种基于自动定理证明的方法,这个方法使用了SAT(布尔可满足性)解法来寻找给定输入程序的性能方面的优化实现。然而这个技术的最坏执行时间复杂度是指数级的,因此只适合短的,性能关键的代码段,如内层循环。
宏展开和窥孔优化结合
在1984年Davidson和Fraser【63】提出了一个高效的指令选择技术,它结合了朴素宏展开的简单性和窥孔优化的高性能。Auslander和Hopkins【24】和Harrison【133】在更早的时候也提出过类似的策略,却没有成功,但是Davidson和Fraser在编译器可重用性和代码质量之间取得了合适的平衡,这使得他们的方法可以成为生产级编译器的合理选择。因此,这个方案变成了知名的Davidson-Fraser方法,并且它的变种已经被用于多个编译器中了,如YC【64】(Davidson和Fraser自己的实现,它也具有RTL级的通用子表达式消除优化),ZEPHYR/VPO系统【14】,Amsterdam Compiler Kit(ACK)【239】,以及 – 最知名的 – GNU编译器工具链(GCC)【157,235】。
Davidson-Fraser方法
在Davidson-Fraser方法中指令选择器由两部分组成:一个展开器和一个合并器(见图2.6)。展开器的任务是将输入程序的IR代码转换成寄存器转移。通过执行一个简单的宏完成转换,它将每个IR节点(假设它是这样表示的)展开成对应的描述节点效果的RTL。不像我们之前研究过的宏展开器,这些宏不包含寄存器分配;而是每个展开器会将结果赋给一个虚拟的存储空间,称为temporary,这种是无限数量的。然后后续的寄存器分配会将每个temporary赋到一个对应的寄存器上,当可用寄存器数量不够的时候,可能需要插入额外的代码将一些值保存到内存中,随后在恢复出来(这个称为寄存器溢出)。但是在做这个之前,合并器为了试着提高代码质量,会尝试将多个RTL合并成一个大的RTL,使用了PO里相同的技术。在运行了合并器和寄存器分配器之后,最后一个过程会输出汇编代码,它将每条RTL替换成相对应的机器指令。但是,对于这个工作,展开器和合并器在每一步都必须遵循机器不变性,即每条已存在的RTL都必须由至少一条目标机器提供的机器指令实现。
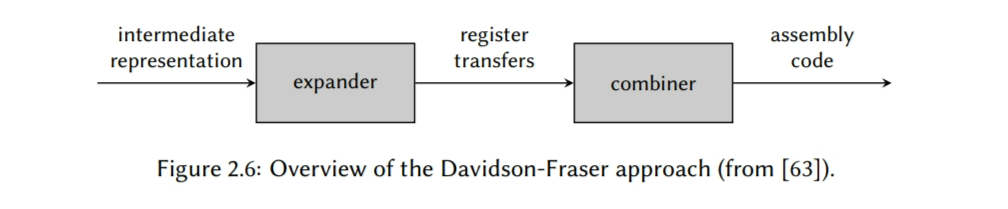
通过使用随后的窥孔优化器合并多条RTL的效果,Davidson和Fraser的指令选择器可以有效地扩展到AST或者IR树的多个节点 – 可能会跨过基础块边界 – 并且它支持的指令数理论上是被窥孔优化器可以同时比较的指令数限制的。例如,如果只能检查两条指令的合并,则将三条指令替换成一条指令的优化它就不支持。但是,增加窗口的大小,通常会增加指数级的开销即增加复杂度,因此,使得复杂机器指令的处理变得更难,因为它需要更大的指令窗口。
后来,Davidson和Fraser工作的改进是由Fraser和Wendt【101】进行的。在1988年的论文中,Fraser和Wendt描述了一个方法,这个方法高效地将展开器和合并器融合成一个单一的实体。基本的想法是将指令选择器分为两步:第一步是产生一个朴素的宏展开器,它一次展开一个IR节点。不像Davidson和Fraser是手写上实现的展开器,Fraser和Wendt使用了一个更简洁的方案,这个方案由一系列的switch和goto语句组成,允许通过机器描述自动生成展开器。生成后,宏展开器将在精心设计的训练集上执行。使用指令选择器内置的函数调用,一个可重用窥孔优化器可以同时执行,它发现并收集特定目标的统计信息,这些可以在已生成的汇编代码上完成。然后,基于这些结果,宏展开器的代码被要求合并有收益的优化决策,因此,允许指令选择器可以高效地一次展开多个IR节点,这就移除了最终编译器对于分离的窥孔优化器的需求。因为指令选择器只需要实现被认为是“有效的”优化决策,所以Fraser和Wendt认为只需要最小的代价就能提高代码质量。后来,Wendt【258】提供了一个更强的机器描述格式从而提升了这个技术 – 也是基于RTL – 随后它演进成了一门更紧凑的独立语言,可用于实现代码生成器(见Fraser【100】).
通过识别器增强机器不变性
最近Dias和Ramsey【70】扩展了Davidson-Fraser的方法。将需要每个分离的面向RTL的优化例程替换为遵循机器无关性的例程,Dias和Ramsey的设计使用了识别器来判断一个优化决策是否违反约束(见图2.7)。这个设计简化了优化例程,因为他们不在需要内部化不变性,所以使得它们中的一些例程可以被自动化生成。
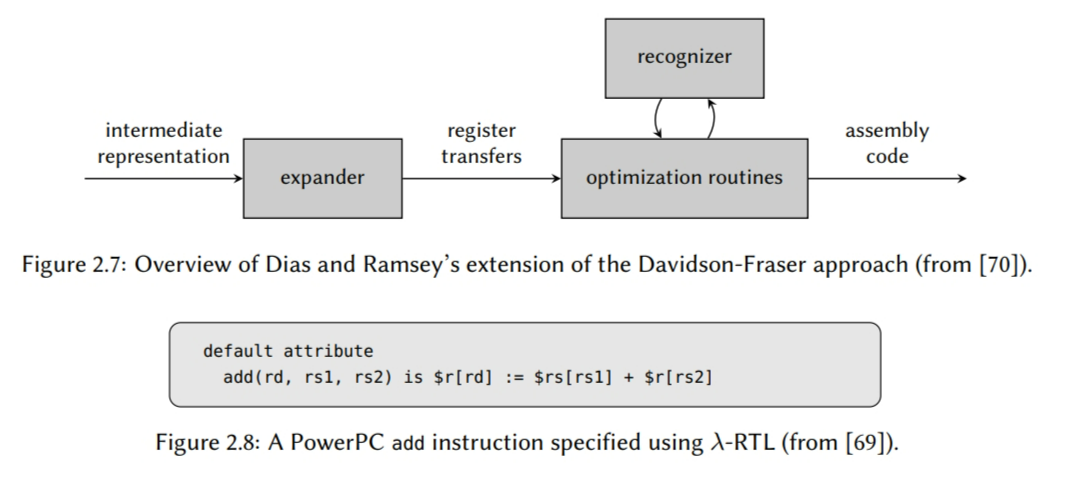
在2006年的论文里,Dias和Ramsey证明了是可以从一个声明式的机器描述自动生成出识别器的,这个描述使用了$\lambda-RLT$。$\lambda-RLT$最初是Ramsey和Davidson【212】开发的,它是一个基于ML的函数式语言,它提高了编写RTL的抽象级别(见图2.8的例子)。根据Dias和Ramsey的说法,基于$\lambda-RLT$的机器描述写起来比其它许多设计更简明和简单,包括GCC。尤其是,$\lambda-RLT$是精确且没有二义性的,这使得它适合于自动化工具生成和验证,后者已经由Fernández和Ramsey【95】以及Bailey和Davidson【25】探索过了。
首先,$\lambda-RLT$是可读的,且它的RTL会被转换成树模式,其类似于表达式树,但建模的是机器指令而不是输入程序。使用这些树模式,则检查一个RTL是否满足机器不变性的任务就简化成一个树覆盖问题。因为整个下一章都专门用于讨论这个问题,所以我们现在只说每个RTL被转换成一个表达式树就足够了,然后表达式树在它的顶部被匹配上。如果表达式树无法完全被模式的任意子集完全覆盖,则这个RTL就不满足机器不变性。尽管这个技术限制了识别器只能在语法级别上推理RTL,但是Dias和Ramsey认为对于效率的要求排除了更加昂贵的语义分析(记住,每个被采用的优化决策都需要使用到识别器)。
一个程序将它们都展开
不久之后,Dias和Ramsey【69,213】提出了一个方案,使得每个特定架构族只需要实现一次宏展开器 – 如基于寄存器的机器,基于栈的机器等 – 它替代了每个特定指令集实现一次宏展开的方案 – 如X86,PowerPC,SPARC等。换句话说,如果两个属于相同的架构族,则可以使用相同的展开器,不需要考虑ISA之间不同的细节。这是有用的,它的正确性只需要被证明一次,因为如果展开器不得不用手写,则证明过程是一个复杂且耗时的一个过程。
这个思路是对于一个特定架构族,需要有一个预定义的特定瓦片集。一个瓦片表示一个简单操作,它对于每个属于这个架构族的目标机器都是必须的。例如,基于栈的机器需要push和pop操作的瓦片,而对于基于寄存器的机器它们就不是必须的。然后,相较于将输入程序里的每个IR展开成一系列RTL,这个展开器会将IR节点展开成一系列的节点。因为相同架构族里的所有机器的瓦片集都是相同,所以展开器只需要被实现一次。在瓦片被输出后,每个瓦片会被实现它们的机器指令所替代,然后产生的结果汇编代码质量可以通过合并器提升。
剩下的问题是对于一个特定目标机器,如何找到实现对应瓦片的机器指令。在同一个论文里,Dias和Ramsey提供了一个自动化做这个替换的方法。通过将瓦片和机器指令都描述成$\lambda - RTL$,Dias和Ramsey开发了一个技术,可以将机器指令的RTL进行合并,这样它们的效果就等价于一个瓦片。从广义上讲,这个算法维护了一个RTL池,它是由机器描述可以找到的RTL初始化的,然后使用序列化(即,将几个RTL合并成一个新的RTL)和代数规则迭代地添加起来。当实现了所有的瓦片,或者遇到某些终止要求之后,这个过程就会停止。后一个要求也是必须的,因为Dias和Ramsey证明了为算术瓦片寻找实现这个通用问题是不可决策的(即,没有算法可以保证终止并找到所有可能的输入对应的实现)。
虽然它的主要目标是提升编译器的可重用性,Dias和Ramsey也展示了他们的设计原型可以产生比GCC的默认Davidson-Fraser指令选择器更好的代码质量。当然,这需要将架构无关的优化关闭掉,因为它们会使得GCC产生更好的结果。
在指令选择之前运行窥孔优化
在刚讨论过的方法里,提升已生成汇编代码的优化例程都是在代码生成之后执行的。但是在Genin等人【118】的方法里,有一个它的变种是在代码生成之前执行的。当目标是数字在信号处理器时,首先它们的编译器会将输入程序转为内部信号流图(ISFG),然后在指令选择之前执行一个模式匹配器,它会试着将ISFG图中几个低级别的操作合并成单个节点,传输更高级别的语义信息(如,循环里一个加法伴随着一个乘法会被合并成一个产品级累加结构)。然后一个节点接一个节点做代码生成:对于每个节点,指令选择器都会调用一条规则以及获取当前上下文的信息。被调用的规则会产生适合于给定上下文的汇编代码,也可以插入新的节点,从而根据插入节点卸载规则更好的处理决策。
根据作者的信息,实验显示他们的编译器生成的代码的速度比当前传统编译器快5到50倍,与手写的汇编代码相当。但是这个设计局限于特定的输入程序,其提前获知的应用信息 – 在数字处理器的场景中 – 可以被编码到特定的优化例程,这很可能必须手动完成。
总结
在这一章中,我们首先讨论了解决指令选择的第一个技术。这些以一种或者另一种基于一种称为宏展开的原理,其中AST或者IR节点被展开成一个或者多个目标架构机器指令。使用模板匹配或者宏调用,这类指令选择器可以被直接实现且高资源利用率的。
但是,朴素宏展开假设IR(或抽象)树和目标机器提供的机器指令之前的节点是 1对1或者1对多映射的。如果存在机器指令可以被标记为n对1的映射,如多输出指令,则这些技术产生的代码质量通常是比较低的。因为机器指令都是彼此独立输出的,所以使用那些对其它机器指令有意外效果的机器指令就变得非常困难(就像前一章描述的相互依赖的指令)。
一个弥补的方法是在代码生成器后端中添加窥孔优化器。这允许汇编代码中多条机器指令被合并,然后替换为更高效的指令,因此可以修正一些指令选择器做出的低效决策。当纳入到指令选择器后 – 一个已知的方法是Davidson-Fraser方法 – 它会使得诸如多输出指令等更复杂的指令被表示成机器描述的一部分。因为它的通用性,Davidson-Fraser方法成为保留到现今的最强大的指令选择方式,一个变种仍然在GCC中使用着。
在下一章中,我们会探讨另一个指令选择的原理,它更直接地解决了使用单个指令实现多个AST或者IR节点的问题。
树覆盖
如同我们在前一章见到的,基于宏展开的大部分指令选择器的主要限制是,展开的范围限制在了表达式树的单一 AST 或者 IR 节点上了。这有效地排除了对许多机器指令的利用,导致了产生的代码质量低。另一个问题是宏展开指令选择器通常将模式匹配和模式选择合并到单步里去了,因此无法考虑机器指令的组合,然后选择产生最”高效“汇编代码的那个。
这些问题可以通过采用另一种指令选择原理来解决,称为树覆盖。这个也是文献中能找到的大部分指令选择技术的原理,从而导致这章是本报告中最长的章节。
原理
让我们假设输入程序是用一组表达式树表示的,这个我们在上一章中已经很熟悉了(见第 10 页)。让我们进一步假设每条机器指令都可以类似地建模成另一个表达式树,然后为了区分通过输入程序建立的表达式树和通过机器指令建立的,我们将后者称为树模式,或简称为模式。然后指令选择的任务就可以归约成寻找一组树模式,使得表达式树上的每个节点都至少被一个模式覆盖了。这里我们可以清楚地看到模式匹配和模式选择组成了指令选择中的两个问题:对于前者,我们需要寻找哪些是适合给定表达式树的树模式;然后对于后者,我们会从这些模式中选出一个子集,生成表达式树的一个有效覆盖。对于大部分目标机器而言,会存在大量的重叠 - 即,一个树模式可能是局部或者全匹配的,节点会被表达式树的另一个模式匹配 - 我们通常希望尽可能少地使用树模式。这有两个原因:
- 争取最少数量的模式意味着选择较大的树模式而不是较小的。这反而使得可以利用更复杂的机器指令,其通常可以生成更高质量的代码。
- 已选择的模式之间的重叠数量是有限的,意味着输入程序中相同操作只在需要的时候被重新实现成多条机器指令。将冗余工作保持到最低限度是提高性能和减少代码大小的另一个关键因素。
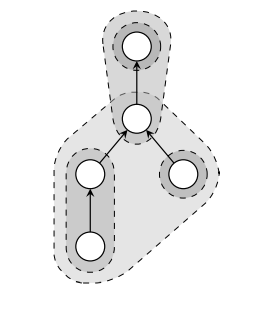
作为一个通用化的最优方案,通常不会定义成最小的已选择模式的数量;而是定义为最小的已选择模式的总开销。这样允许选择的模式开销可以适应所需优化的标准,虽然模式数量和总开销之间总是有强的相关性。但是,如同第 1 章强调的,被认为是指令选择的最佳解决方案的,不一定是最终汇编代码的最佳解决方案。而且,我们只能考虑存在合适的树模式的机器指令。寻找树匹配问题的最优方案不是一个平凡的任务,如果只允许某些模式组合存在,它会变得更少。可以确定的是,大多数人都很难相处一种有效的方法可以找到所有的有效树模式匹配。因此,我们从探索解决第一个方法开始,其可以解决模式匹配的问题,但不一定可以处理模式选择的问题,然后逐渐过渡到可以做到这些事情。
第一种使用树模式匹配的技术
1972 年和 1973 年 Wasilew[255] 和 Weingart[256] 发表了已知的第一篇使用树模式匹配来描述代码生成技术的论文(由于缺乏第一手资料,我们在本报告中将仅讨论两者中的前者)。根据 [45,116] Weingart 的设计使用了单个模式树 – Weingart 称这个为歧视网 - 它是从一个声明性的机器描述中自动派生出来的。使用单个树,Weingart 认为,是一种紧凑而有效的表示方式。然后构建 AST 的过程被扩展成同时将每个新的 AST 节点压入栈上。当一个新节点出现时,通过比较栈上的节点和模式树种的当前节点的子节点,逐步遍历模式树。当一个搜索过程到达模式树的叶子节点时,就找到了一个模式匹配,于是输出匹配关联的机器指令。
比起早期的宏展开指令选择器(即,DavidsonFraser 之前的那些),Weingart 的方法扩展了机器指令以支持那些扩展到多个 AST 节点的指令。但是,这个技术实际应用中遇到了几个问题。首先,对于特定的目标机器,构造模式树满足高效的模式匹配被证明是困难的;众所周知,Weingart 特别与 PDP-11 作斗争了。第二,它假设目标机器上至少存在一条机器指令与 AST 上的一个特定节点类型对应,但是对于某些特定编程语言和目标机器的组合,事实证明并非如此。Weingart 通过引入额外的模式部分地解决了这个问题,称为转换模式,它使得 AST 上不匹配的部分被转换成,有希望被某些模式匹配的形式,但是这个不得不手动做,有可能会使得编译器陷入无限循环中。第三,就像它的前辈宏扩展一样,一旦找到匹配项,该过程就会立即选出一个模式。
另一个早期的模式匹配技术是由 Johnson [143] 开发的,实现在 PCC(可移植的 C 编译器)上了,它是一个著名的系统,是第一个与 Unix 一起发布的标准 C 编译器。Johnson 基于 Snyder[233] 早期做出的 PCC – 它是我们在上一章的 2.2.2 节讨论过的 – 但是用基于树重写的技术替换了朴素宏展开的指令选择器。对于每个机器指令,表达式树是和重写规则,子目标,资源需求,以及逐字输出的汇编字符串一起形成的。这些信息通过一个机器描述给出,如图 3.1,允许多个简单的模式浓缩成一个简单的声明。
然后模式匹配相对就直接了:对于表达式树中一个给定的节点,这个节点与每个模式的根节点比较。如果匹配上,则对模式中的相关子树都做类似的检查。只要模式中的所有叶子节点都可达,则找到一个匹配。因为这个算法 – 图 3.2 给出了它的伪代码 – 展示了二次方的执行时间,尽量减少冗余检查的数量是有帮助的。这是通过维护一组代码目标来完成的,这些目标以整数的形式编码到了指令选择器中。因为历史原因,这个整数被称为cookie,每个模式都有相关的 cookie 表明它在哪个场景下是有效的。如果 cookies 和模式都匹配上,则尝试分配模式所需的任意资源(如,如果一个模式可能会需要任意数量的寄存器)。如果成功,则输出相应的汇编字符串,然后表达式树中的已匹配节点被替换成重写规则指定的单个节点。匹配重写的规则一直重复直到表达式树只由单个节点组成,这意味着整个表达式树已经成功地被转成汇编代码。但是,如果没有模式匹配上,指令选择器会进入一个启发式模式,其中表达式树会被部分地重写直到找到一个模式。例如,为了匹配一个 a = reg + b 的模式,一个 a += b 的表达式首先被重写为 a = a + b,然后另一个规则尝试强制一个操作数放入寄存器中。


虽然它在当时是很成功的,但是 PCC 有几个缺点。就像 Weingart,Johnson 的技术使用了启发式重写规则来处理不匹配的场景。缺乏形式化的验证方法,当前的规则集总是存在不足的风险,并可能会导致编译器永远无法终止某些输入程序。Reiser [215] 还指出了,其所研究的 PCC 版本仅支持具有最大高度为 1 的一元和二元模式,因此,排除了许多带有复杂地址模式的指令。最后,PCC – 以及目前为止讨论的所有其它方法 – 在选择模式时依旧坚持着第一匹配第一个使用的原则。
使用 LR 解析自下而上覆盖树
如之前所述的,第一种方式中的一个常见缺陷是(i)他们应用了最贪婪的模式选择,(ii)且通常缺乏正式的方法论。相反,语法分析 – 这是解析输入程序源码的任务 – 可以说是最好理解的编译领域了,且它的方法也产生了完全由表驱动的解析器,这种解析器非常快速且资源高效的。
Glanville-Graham 方法
1978 年 Glanville 和 Graham [121] 提出了一篇开创性的论文,描述了语法分析技术是如何可以用到指令选择上的。后续的实验和评估表明这种设计 – 我们将其称为 Glanville-Graham 方法 – 被证明比当代方法[9, 116, 126, 127]更简单、更通用。而且,由于其表驱动的性质,汇编代码可以快速地生成(虽然第一个实现与当时使用的其它指令选择器相当)。最后,Glanville-Graham 方法已经被认为是这个领域最重要的突破之一了,并且这些想法以某种方式影响了许多后来的技术。
将机器指令表示为语法
首先,移除算术表达式中必要括号而不会导致歧义的一个已知方法是使用波兰前缀表示法。例如,$1+(2+3)$ 可以写成$+1+2\ 3$,含义是相同的。Glanvile 和 Graham 意识到使用这种形式机器指令可以被表达成一个基于 BNF(Backus-Naur 范式)的上下文无关语法。这个概念在大多数编译器书本中都有很好的描述 – 我推荐的[8] – 因此我们只进行一个简短的介绍。
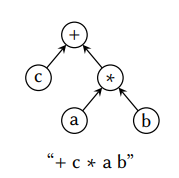
一个上下文无关的语法由一组终结符和非终结符组成,这两个我们都称为符号。我们将会通过不同的书写方式来区分两者,总是以首字母大写的方式来书写终结符(如,Term),而非终结符整个都是小写的形式(如,nt)。对于每个非终结符都存在一个或多个如下形式的产生式:
$$
lhs \rightarrow Right\ hand\ Side …
$$
产生式基本上指定了如何用另一个非终结符(左侧)替换一组特定符号组合(右侧)。由于非终结符可以出现在产生式的两边,因此大部分语法允许无限的替代链,这是上下文无关语法一个强大的特性。从递归的角度而言,也可以将非终结符视为递归的场景,而终结符当作是停止递归的场景。产生式也被称为产生规则或者规则, 尽管它们通常可以互换而不会引起混淆,但是我们将在本报告中保持一致,仅使用第一个术语,因为规则的含义略有不同。
为了将一组指令建模为上下文无关语法,给每条指令添加一条或多条规则。我们称这个规则集合为指令集语法。每条规则包含了一个产生式,开销,和一个动作。产生式的右侧表示要在表达式树上匹配的树模式,左侧包含的非终结符,用来表示执行机器指令的结果的特征(如一个特定的寄存器类型)。此处的开销就含义明了的,而动作通常是输出一个汇编字符串。我们用一个带注释的示例更简洁地说明规则的结构:
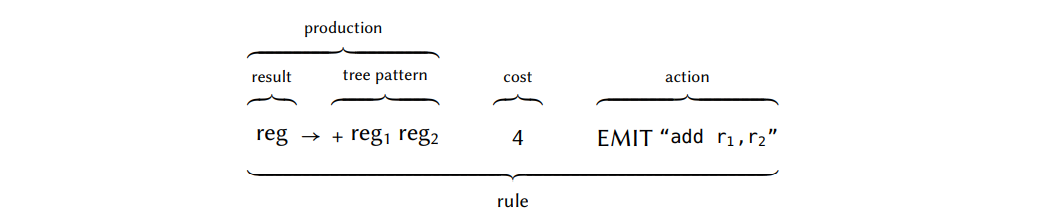
在大多数的文献中,规则和模式通常是有相同含义的。但是,在这篇报告中,处于语法上下文的一条规则是一个包含产生式,开销,和动作的三元组,而一个模式指的是出现在规则中的产生式的右侧内容。
树解析
指令集语法给我们提供了一个形式化建模机器指令的方法,但是它没有解决模式匹配和模式选择的问题。对于这个问题,Glanville 和 Graham 应用了一个已知的技术,LR parsing(左到右,最右边归约)。因为这个技术主要与语法解析相关,所以应用到树上的相同方法通常称为树解析。我们继续举一个例子。
让我们假设我们有下面的指令集语法

然后我们想要产生如下表达式树的汇编代码
$$
+\ c\ \ a\ b
$$
使得表达式的结果最终在寄存器中。如果 a,b,和 c 都是整形,则我们可以假设表达式树上的每个节点都是 Int 类型,,或者 +;这些将会是我们的终结符。
在将表达式树转换为终结符序列后,我们从左到右依次遍历每一个。在这个过程中,我们要么将刚刚遍历到的符号放到栈上,或者通过一个规则归约替换当前栈上的符号。一个归约操作有两部分组成:首先根据出现在规则右侧的内容弹出符号。数量和顺序必须与一条有效的归约规则匹配。弹出后,出现在左侧的非终结符将被压入到栈上,同时也会输出与规则相关联的汇编代码(如果有)。对于一个给定的输入,执行规则归约也可以被表示成一个解析树,演示了用于解析这颗树的终结符和非终结符。现在,回到我们的用例,如果我们用 s 表示一个转换,以及用 $r_x$ 表示一个归约,其中 x 是归约规则的数量,则表达式树 ”+ Int(c) * Int(a) Int(b)“ 的一个有效树解析是:
$$
S\ S\ S\ r_3\ r_2\ S\ r_3\ r_1
$$
证明这个式子作为一个习题留给读者解决。对于这个特定的树解析,相关的解析树和产生的相关汇编代码如下:
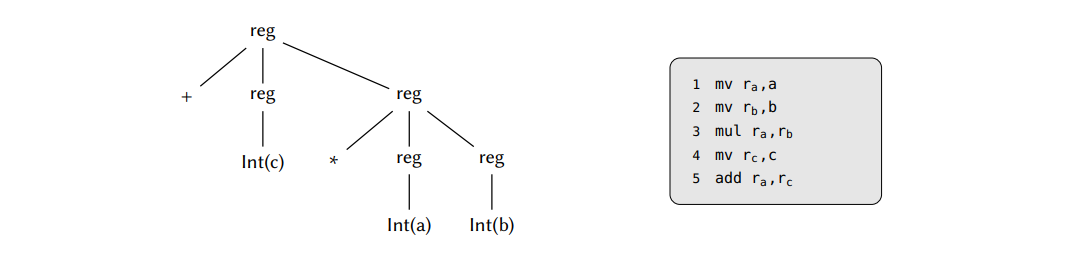
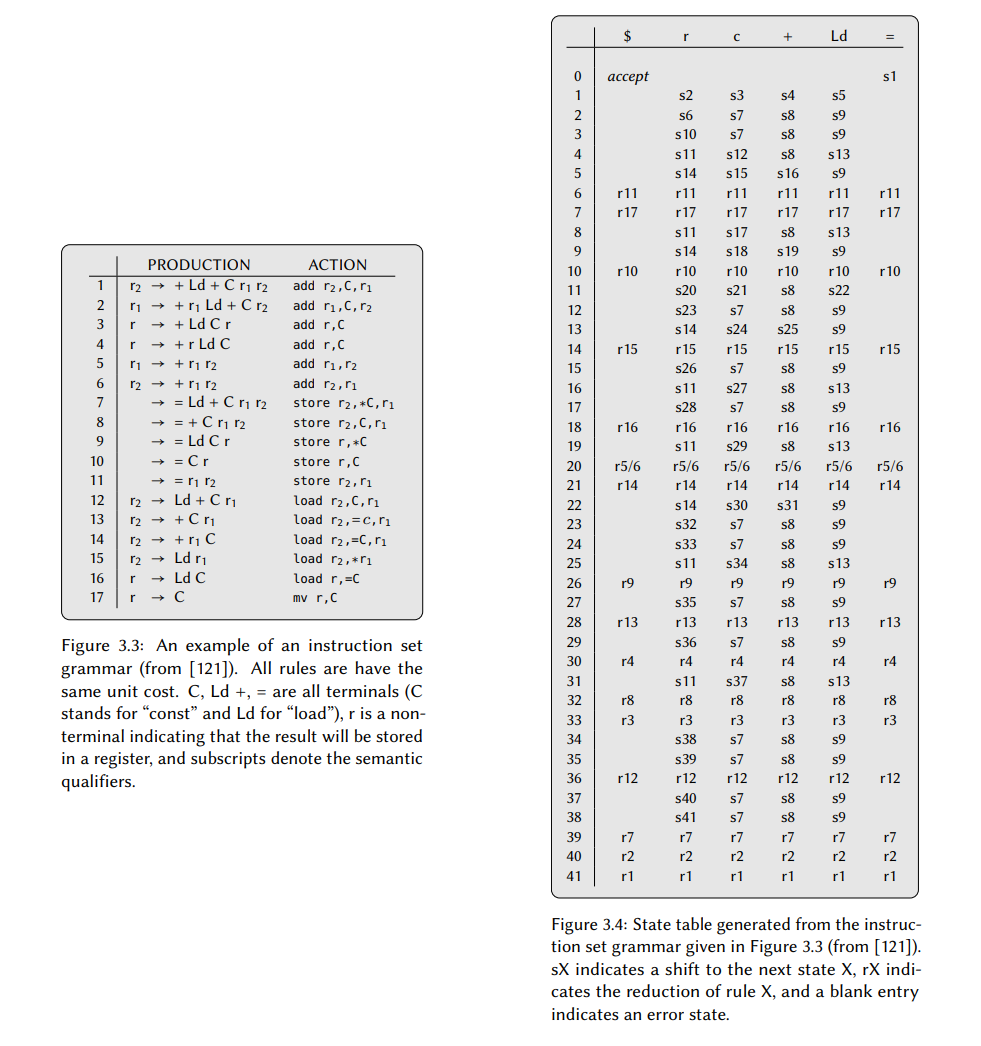
剩下的问题是如何知道何时转换以及何时归约。这个可以通过查阅特定语法生成的状态表来。这个表是如何生成的已经超出了本报告的范围,但是会在图 3.4 中给出一个例子,它是由图 3.3 中的指令集语法生成的。然后图 3.5 给出了一个使用这个状态表执行指令选择器的过程。图 3.3 中的一些产生式里出现的下标是语义限定词,它用于表达可能会出现在机器指令中的语法限制。例如,所有的双地址算术机器指令都将结果存储到作为输入提供的寄存器中的一个,然后使用语法限定词它可以表达为 $r_1 \rightarrow + r_1\ r_2$,表明目的寄存器必须与第一个操作数相同。为了让这个信息在解析期间是有效的,解析器将其与它相关联的终结符或非终结符符号一起放到栈上。Glaville 和 Graham 也整合了一个寄存器分配器到他们的解析器中,因此,给出了整个代码生成的后端。
解决冲突和避免阻塞
一个指令集语法通常是由二义性的,意味着相同的表达式树可能会存在多个有效的树解析,这会导致解析器可能会存在一个可以执行移位也可以执行归约的情况。这被称为移位归约冲突,是一个非正交的 ISA 会出现的结果。为了解决这种冲突,Glaville 和 Graham 的状态表生成器总是选择移位。直观上,这会有利于较大的模式而不是较小的模式,因为一个移位推迟了模式选择的决策,同时允许有关表达式树的更多信息堆积到栈上。
同样地,也可能存在一个归约归约冲突,即解析器在一个归约选择规则的时候存在两个或多个选择。Glaville 和 Graham 通过选择有最长右侧的规则来解决这个问题。如果语法包含的规则仅在它们的语法限定词上不同,则仍然存在超过一条规则可以归约(在图 3.3 中,规则 5 和 6 就是两条这样的规则)。解析期间里可以解决这个问题,方法是在这个期间里按它们出现在语法中的顺序检查语法限制(例如,参考图 3.4 中的状态 )。但是,如果这个集合中的所有规则都是有语法限制的,则会出现解析器无法选择任意一条规则的情况。这种情况称为语义阻塞,必须要提供一条默认的规则才能解决这个问题,这条规则会在除它以外的所有情况都失败的情况下被调用。这种回退规则通常使用多个,较短的机器指令来模拟比较复杂的规则的效果,然后 Glanville 和 Graham 设计了一个精妙的技巧来自动推导它们:对于每个语义约束规则,树解析是在表示该规则右侧的表达式树上进行的,然后使用为实现该树而选择的机器指令来构成回退规则。

优势
通过依赖状态表,Glanville-Graham 形式的指令选择器是完全表驱动的,由基本上是一系列表查找组成的核心实现。故而,指令选择器产生汇编代码需要花费的时间是线性于表达式树的大小的。尽管表驱动代码生成的想法并不新颖 – 我们在之前的章节中已经见过一些了 – 但是早期的尝试为产生表提供一个自动化的过程都失败了。此外,许多与模式选择相关 的决策都是在状态表生成时解决移位-归约冲突和归约-归约冲突来预先计算的,这会使得编译更快。
Glanville-Graham 方法的另一个优势是它的形式化基础使得自动化验证的方式成为可能。例如,Emmelmann [80] 提出了证明指令集语法完整性的方法,这个方法是第一批验证方法中的一个。直观上,Emmelmann 自动化证明法是寻找所有的可以出现在输入程序但不能被指令选择器处理的表达式树。让我们将指令集语法表示为 $G$,描述表达式树的语法表示为$\tau$。如果我们进一步用 $L(x)$ 来表示所有能被语法 $x$ 接受的树的集合,则我们可以通过检查 $L(\tau)/L(G)$ 是否生成非空集来确定指令集语法是否完整。Emmelmann 认识到这个交叉可以通过创建一个生成自动机来计算,这个自动机本质上是实现了只接受这组反例中的树的语言。Brandner [34] 最近扩展了这个方法来处理包含称为谓词的动态检查的产生式 – 我们将在探索属性语法时简短地讨论 - 通过拆分终结符来暴露这些隐藏的特性。
劣势
虽然 Glanville-Graham 方法解决了几个当前的指令选择技术的问题,但是它也有自己的劣势。首先,由于解析器只能对语法进行推理,因此关于特定值或者范围的任何限制都必须赋予它自己的非终结符。与限制结合则每个产生式就可以只匹配到单个的树模式,这通常意味着,对于带有几个地址或者操作数模式的多功能机器指令的规则对于每个这样的结合都要重复一份。但是,对于大部分的目标机器,这被证明时不可行的;在 VAX 机器的场景中 – 基于 CISC 的架构开始于 1980 年代,每条机器指令都接受多个操作数模式 [48] – 因此一个指令集语法将会包含超过八百万条规则[127]。重构 – 通过非终结符表达共享特征来合并相似规则的任务 – 会将这个数量降低到大约只有千条规则左右,但是这个不得不做得非常小心,从而避免对代码质量有负面的影响。第二,因为解析器从左往右遍历没有回溯,所以必须在其它任意操作数可以观察到前,先输出一个操作数的汇编代码。这会导致一个比较坏的决策,在之后会取消然后输出另外的代码。因此,设计一个紧凑的指令集语法 – 其也会产生好的代码质量 – 语法作者必须对指令选择器的内部工作有广泛的了解。
使用语义处理扩展语法
在纯的上下文无关语法中,是完全无法处理语义信息的。例如,用 reg 非终结符表示一个明确的寄存器是做不到的。Glanville 和 Graham 通过将信息放到栈上来解决这个限制,但即使这样,他们修改后的 LR 解析器也只能使用简单的等式比较进行推理。Ganapathi 和 Fischer [112, 113, 114, 115] 通过将传统的上下文无关语法替换为更强大的语法集即属性语法,来解决这个问题。就像 Glanville-Graham 方法,我们将只会在顶层讨论它是如何工作的;对细节感兴趣的读者建议去进一步了解相关的论文。
属性语法
属性语法 – 或者他们也称为词缀语法 – 是 Knuth 在 1968 年引入的,他将上下文无关语法扩展成带有属性的。属性用于存储,操纵,以及在解析期间传播关于独立的终结符和非终结符的额外信息,然后一个属性要么是合成的要么是继承的。使用解析树作为参考点,带有同步属性形式的节点的值来自于它的子节点的属性,带有继承属性的节点的值拷贝自子节点的值。因此,合成属性的信息沿着树向上流动,而继承属性的信息沿着树向下流动。故我们通过 $\uparrow$ 和 $\downarrow$ 分别区分合成属性和继承属性, 这两个会标注为特定符号的前缀(如,一个 reg 非终结符的 x 合成属性写为 reg $\uparrow$ x)。
然后这个属性用在谓词和动作里。谓词用于检查一个规则的适用性,动作用于产生新的合成属性。因此,当建模机器指令的时候,我们使用可以谓词来表示约束,使用动作来表明效果,如代码输出和结果会被存储到什么寄存器里。让我们看个例子。
在图 3.6 中,我们看到一组建模三个字节加法机器指令的规则:一个增量版本 incb(将寄存器递增 1,由规则 1 和 2 建模);一个两地址的版本 add2b(加两个寄存器和存储结果到其中一个操作数中,由规则 3 和 4 建模);一个三地址版本 add3b(结果可以存储到其它地方,由规则 5 建模)。自然地,incb 指令只能被用到其中一个操作数是 1 的场景下,这个值是通过谓词 IsOne 强制限制的。此外,因此这条指令破坏了这个寄存器的前一个值,只有后续的指令不会在使用到这个旧值,才可以使用这条指令;这被谓词 NotBusy 强制执行。然后 EMIT 动作输出相关的汇编代码。因为加法是可交换的,我们需要两条规则来使得机器指令适用于这两种情况。类似地,我们在 add2b 指令上也有两条规则,但是谓词被替换成了TwoOp,它会检查是否其中一个操作数是赋值目标,或者这个是否后续不需要了(即,它不忙了)。 因为,最后一条规则没有任何的谓词限制,所以它也作为默认规则,从而防止出现我们之前讨论的在覆盖 Glanville-Graham 方法时出现的语义阻塞的情况。

优缺点
使用谓词就不需要在为了表达特定的值和范围而引入新的非终结符,这使得指令集语法更加简明。在 VAX 机器的场景中,属性的使用导致了语法大小只有 Glanville-Graham 方法需要的一半,并且没有大量的重构[113]。属性语法也促进了机器描述的增量开发:它可以从实现最通用的规则开始,以实现生成正确但效率低下的代码的指令集语法。然后处理更复杂的机器指令的规则可以增量地添加,因此可以平衡实现工作量和代码质量。另一个很好的特性是其它的优化例程,如常量折叠,可以表示为语法的一部分,而不是单独的组件。
但是,为了允许属性和 LR 解析器一起使用,必须限制指令集语法的属性。首先,只有合成属性可以出现在非终结符中。这是因为 LR 解析器是自底向上,从左往右的构造解析树的,从叶子开始,向上延伸到根部。因此,用于指导子树构建的继承值只有在子树已经创建之后才可用。第二,因为谓词可能会使得一条规则对规则归约无效,所以所有的动作必须出现在产生式的最右侧;否则,可能会导致无法取消的不正确效果。第三,与 Glanville-Graham 方法一样,解析器必须对一个子树做出决定,而不考虑可能出现在右侧的兄弟子树。因此,如果所有的子树事先都是有效的,则它可以提高汇编代码的质量,这是由于使用了 LR 解析的又一个限制。后来 Ganapathi [111] 做了一个解决这个问题的尝试,使用 Prolog 来实现指令选择器 – Prolog 是一个逻辑编程语言 – 但这导致了指数级的最坏运行时间。
维护多个解析树而获得更好的代码质量
因为 LR 解析器只对表达式树进行了一次遍历 – 因此只产生了许多可能的解析树中的一个 – 产生的汇编代码严重地依赖于指令集语法来指导解析器寻找到 “好的” 解析树。
Christopher 等人[52] 尝试解决这个问题,通过使用 Glanville-Graham 方法的概念,但是扩展了解析器以生成所有的解析树,然后选择能生成最好汇编代码的那个。这是通过将原来的 LR(1)解析器替换为 Earley 的算法 [74] 来达成的,虽然这个方法某种程度上提高了代码质量 – 至少理论上 – 但它是以枚举出所有解析树为代价的,这在实际中是非常昂贵的。
在 2000 年,Madhavan 等人[181] 扩展了 Glanville-Graham 方法来获得一个最优的模式选择,同时据称保留了 LR 解析的线性时间复杂度。通过引入一个新版本的 LR 解析[230],之前在找到一条匹配规则会直接执行的归约,现在允许推迟任意的步数。因此,指令选择器本质上还是追踪了多个解析树,允许它在做出可能证明是次优决定之前,可以收集足够多的关于输入程序的信息。换句话说,类似于 Christopher 等人的,Madhavan 等人的设计也会覆盖所有的解析树,但会立即丢弃掉被确实是产生低效汇编代码的解析树。为了有效地做到这点,该方法还引入了离线开销分析,我们将在后面的 3.6.3 节中讨论到这个。最近,Yang [266] 提出了一个相似的技术,涉及到解析树仙人掌[sic]的使用,其中偏离的解析树从公共主干分支出来,从而减少了需要的空间。但是,两种的基本原则仍然禁止建模许多典型的目标机器特性,如多输出指令。
使用递归自顶向下覆盖树
到目前为止检查过的树覆盖方法 – 特别是那些基于 LR 解析的 – 都是自底向上操作的:指令选择器从覆盖表达式树的叶子节点开始,然后基于这些决策,它随后覆盖了剩余的子树直到它到达根,沿途不断匹配和选择适用的模式。这绝不是唯一的覆盖方法,因为它也可以自上而下地完成。有这样一种方法,指令选择器从根节点开始覆盖表达式树,然后递归向下进行匹配。最后,语义信息的流动(如,会存储结果的特定寄存器)也是不同的:自底向上的指令选择器让这些信息沿着表达式树向上扩散 – 通过辅助的数据结构或者树重写 – 而自顶向下的实现会实现决定这个并向下推进。因此,后者被认为是目标驱动的,因为模式选择是由一组额外的需求引导的,而这些需求必须由所选的模式满足。因为,这反过来会对子树产生新的需求,所以大部分的自顶向下的技术都是使用带有回溯的递归实现的。这是必须的,因为某些模式的选择可能会导致低级别的表达式树变得无法被覆盖。
第一个方法
手段-目的分析指导指令选择
据我所知,Newcomer[194] 是第一个开发了使用自顶向下覆盖的方法来解决指令选择问题的人。在他 1975 的博士论文中,Newcomer 提出了一个设计,能详细地找出所有覆盖给定表达式树的模式的组合,然后选出一个最小开销的。Cattell[45] 也在他的调查文章中描述了这些,这是本次讨论的主要来源。
机器指令被建模成T-operators,其基本上是附带了成本和属性的树模式。这个属性描述了各种限制,如哪个寄存器可以用于操作数上。也有一组指令选择器用于执行输入程序必要的转换的 T-operators – 随着我们的进一步讨论这个需求会变得清晰。使用这个工具集,该方案将 AST 作为期望的输入,然后按之前说的自顶向下的方法转换它:指令选择器尝试为 AST 的根节点找到所有匹配的模式,然后进一步递归地覆盖每个匹配剩余的子树。模式匹配是使用我们以前知道的一种直接技术完成的(见 25 页图 3.2),然后为了高效,所有的模式都根据它们的根节点类型进行标注。因此,这个过程的结果是一组模式序列,其中每个都覆盖了整个 AST。然后,检查每个序列是否每个模式的属性都是等于首选属性集(PAS),其因此对应于目标。否则,指令选择器将尝试使用 T-operators 转换重写子树直到属性匹配上。为了指导这个过程,Newcomer 应用了一个启发式规则称为手段目的分析,它是 Newell 和 Simon [195] 在 1959 年介绍的。 手段-目的分析背后直观上是递归地最小化数量差异 – 如何计算的没有在 [45] 中提到 – 在当前状态(即,子树现在的样子)和目标状态(它应该成为的样子)之间的。为了避免无限循环,当转换过程到达搜索空间中的特定深度,它就会停止。如果成功,则应用的转化会被插入到模式序列中;否则丢弃掉序列。从被找到的模式序列中,选出总开销最低的,随后是代码输出。
作为手段-目的分析的应用,Newcomer 的方法是开创性的,让它可以指导输入程序的修改过程直到它可以在特定目标机器上实现,而不需要特地采用特定目标机制。但是,这个设计并非没有缺陷的。首先,这个设计几乎没有实际的应用,因为它只能处理算术表达式。第二,用于建模机器指令的 T-operators 和转换相同,也不得不手动构造,这是非平凡的,阻碍了编译器的可移植性。第三,由于搜索空间的截断,转换输入程序的过程可能会过早地结束,导致指令选择器无法生成任何的汇编代码。最后,事实证明除了最小的输入树外,搜索策略的代价太高因而无法在实践中使用它。
让手段-目标分析在实际中可用
Cattel 等人[44,47,176]后来提高和扩展了 Newcomer 的工作,使之成为一个更实用的框架,被实现在产生质量编译器-编译器(PQCC)中,Bliss-11 编译器的衍生版本,最初是由 Wulf 等人实现的 [264]。他们的方法不是在编译输入程序的时候执行手段-目的分析,而是在生成编译器本身的时候将其作为预处理步骤 – 更类似于 Glanville-Graham 方法。
模式由一组模板表示,这些模板使用递归组合形成,因此类似于指令集语法中的产生式。但是不像 Glanville 和 Graham 以及 Granapathi 和 Fischer 的设计,模板不是手写的,而是根据特定的机器描述自动生成的。每个机器指令描述为一组机器操作,其描述了指令的效果,因此类似于前一章中的 Fraser [102] 介绍的 RTLs。 然后这些效果被一个称为 CGG(代码生成器的生成器)的分离工具用于创建模板,而模板被指令选择器所使用。为了产生与机器指令直接对应的平凡模板,CGG 也会产生一组单节点模式和一组结合了多个机器指令的巨大模式。前者保证了指令选择器可以为所有的输入程序生成汇编代码,因为任意的表达式树都可以简单的被覆盖;而后者可以降低编译时间,因为比起多个小的匹配,直接匹配一个大的模式更快。为了实现这个,CGG 组合使用了手段-目的分析和启发式规则,其应用了一组公式(如,$\neg\neg E\Leftrightarrow E,\ E+0\Leftrightarrow E,\ \neg(E_1 \ge E_2) \Leftrightarrow E_1\lt E_2$)来操作和合并存在的树模式。但是,不保证“感兴趣”的树模式都是永远适用的。一旦生成,则指令选择器就会以贪婪的,自顶向下的方式执行,它总是选择与表达式树中的当前节点相匹配的最小开销的模板(模板匹配使用的方法与 Newcomer 的方法完全相同)。如果出现平局,则指令选择器会选择内存加载次数最少的模板。
与之前讨论的基于 LR-解析的方法相比,Cattell 等人的方法也由优缺点。主要的优点是无论提供了模板是什么,产生的指令选择器总是能够为所有可能的输入树生成有效的汇编代码。至少在 Granapathi 和 Fischer 的设计中,语法设计者必须保证这个正确性。缺点是它的速度相当的慢:基于树解析的指令选择器在模式匹配和模式选择两个方面都是线性时间复杂度的,而 Cattell 等人的指令选择器不得不单独的匹配每个模板,在最坏时间复杂度下是需要2次方的时间。
最近的技术
据我所知,最近唯一使用这种递归自顶向下的方法进行树覆盖的方案是 Nymeyer 等人的[197, 198]。在 1996 和 1997 两篇文章中,Nymeyer 等人描述了一个方法,A* 搜索 – 另一个控制搜索空间的策略(见[219])– 和自底向上重写系统理论相结合的方法,或者简称为 BURS。我们将会在本章的后续内容中详细地讨论 BURS 理论 – 着急的读者可以直接跳到 3.6.3 节中 – 当下只要提到基于 BURS 的语法允许的转换规则就足够了,如会包含将 $X\ +\ Y$ 重写为 $Y\ +\ X$ 的规则,这可能会简化和减少表达机器指令需要的规则数。但是,作者没有给出任何的实验数据,从而难以判断 A*-BURS 理论的组合是否是在实际中可以应用的技术。
树重写和树覆盖的说明
在这个时候,有些读者可能会觉得树重写 – 其中模式被迭代地选择以重写表达式树,直到它由某个目标类型的单个节点组成 – 与树覆盖是完全不同的 – 其中合适的节点会被选出来覆盖表达式树中的所有节点。事实它们确实存在着些许不同,但是对于使用树重写表达的问题是有效的方法,对于等价的用树覆盖表达的问题也是有效的,反之亦然。因此可以认为两者是可以互换的。但是我认为树重写是解决树覆盖问题的一种方案,而树覆盖才是基本的原则问题。
分离的模式匹配和模式选择
在前面讨论树覆盖方法里,模式匹配任务和模式选择任务被统一到了同一个步骤里。虽然这个允许代码生成在单阶段就可以完成 – 一个已经过时的潮流[227] – 但它通常也使得指令选择器无法考量到模式组合之间的影响。通过将这两个关注点分开,并且允许指令选择器在表达式树上运行多次,使得它可以在做出不明智决定之前,就收集到足够多的所有可用模式的信息。但是除了 LR 解析,目前我们看到的所有模式匹配器都是二次方复杂度的算法实现。幸运地是,我们可以做得更好。
线性时间树模式匹配算法
这些年来,已经发现了许多算法可以找到一组给定树模式在另一个给定树能匹配到的所有情况(例如[51,55,73,140,149,210,211,229,257,265])。但是在树覆盖中,大部分的模式匹配算法都是源自字符串模式匹配方法的。它是由 Karp 等人[149] 在 1972 年首次发现的,然后 Hoffmann 和 O’Donnell [140] 扩展这些思想形成基于树。的指令选择技术最常用的算法。所以为了树的指令模式匹配,让我们首先探索下字符串是怎么做的。
匹配树和匹配字符串是相同的
Aho、Corasick[5] 和 Knuth 等人[160] 引入的算法最常见地是用于字符串匹配。其它独立的发现是在 1975 年和 1977 年分别发表的,两个算法操作方式是相同的,因此它们的方法几乎是相同的。直观上看是,当一个有重复模式的子字符串局部匹配失败,匹配器不需要总是返回到匹配初始开始的位置的输入字符。这里有个内置的图表演示了子字符串 abccbd 匹配上输入字符串 abcabcabd 的情况。箭头表示正在处理的字符。首先,子字符串从输入字符串的开头开始匹配,直到最后一个字符串(位置 5)。当它失败的时候,不是直接返回到位置 1 从头开始重新匹配,而是匹配器记住了子字符串的前三个字符(abc)已经在这个时候匹配上了,因此继续匹配位置 6,尝试匹配子字符串的第四个字符。因此,所有子字符串情况都可以在线性时间里找到。后面以 Aho 和 Corasick 的方法继续我们的讨论,因为它可以匹配多个子字符串,而 knuth 等人的算法只考虑了单个字符串(虽然它也可以简单地扩展成处理多个字符串的场景)。
Aho 和 Corasick 的算法依赖三个函数 – goto,failure,和output – 其中第一个实现了一个状态机,后面两个是简单的查找表。它们是如何构造的已经超出了本篇的范围 – 读者可以查阅相关的论文 – 但是我们会用一个例子演示它们是如何工作的。在图 3.7 中,我们会看到匹配字符串 he,she,his 和 hers 的相关函数。当一个字符从输入字符串 shis 读取到,它首先作为 goto 函数的参数,这个状态机被初始化到状态 0 上。s 作为输入时它转换成了状态 3,然后 h 会使得它停止在状态 4 上。但是,对于下一个输入 i,不存在从当前状态出去的相关边。在这个时候,会去调用 failure 函数,它表明状态机应该回退到状态 1。我们在这个状态重试 i,它会让我们到达状态 6,接着用最后输入的字符就可以转换到状态 7。对于这个状态,output 函数也表明了我们可以找到这个模式的一个匹配字符串 his。
Hoffmann-O’Donnell 算法
Hoffmann 和 O’Donnell [140] 开发了两个算法,包含了 Aho 和 Corasick 与 Knuth 等人的想法。在他们 1982 年的文章中,首次提出了一个 $O(np)$ 的算法以自顶向下的方式匹配树模式,然后是一个 $O(n + m)$ 自底向下算法以线性模式匹配交换更长的预处理时间(n 是主题树的大小,p 是树模式的数量,m 是找到的模式数量)。
字母的模式匹配 – 因为它的线性运行行为所以应用最广泛 – 是比较简单的,如图 3.8 所示:从叶子节点开始,每个节点都被标记了一个标识符,表示与该节点的子树根匹配的一组模式。我们称这个集合为 matchset。赋给一个特定节点的标签是可以被检索到的,通过将子节点的标签作为表的索引即可,它对于当前节点的类型是特定的。例如,表示加法节点的表完成查找用的是一张表,而表示减法节点完成查找用的是另一张表。表的大小取决于节点拥有的孩子数量,如二元操作节点有个二维表;而表示常量的节点有个零维的表,因此只有一个值组成。第 41 页图 3.9 (g)也提供了一个全的标签例子。然后通过随后的自顶向下遍历检索匹配集。
因为 Hoffmann 和 O’Donnell 引入的自底向上算法对指令选择有了历史性的影响,所以我们会花费一些时间讨论标签的查找表是如何生成的细节。
定义
我们从介绍一些定义开始,为了帮助我们理解,我们使用两个树模式,分别出现在图 3.9 (a)和(b)中的 I 和 II。首先,我们认为模式 I 和 II 构成了我们的模式簇,由带有符号 a、b、c 和 v 的节点组成,其中 a 节点确定由两个子孩子,b,c 和 v 没有。v 符号是一个特殊的 nullary 符号,表示一个可以匹配任何子树的节点。这些符号共同构成了模式簇的子母表,我们将其表示为 $\sum$。字母表必须是有限的并且需要排序,意味着 $\sum$ 中的每个符号都有一个排序函数,它给出了每个给定符号的子孩子数量。因此,在我们的场景中,$ rank(a) = 2$ 且 $ rank(b) = rank(c) = rank(v) = 0$。遵循 Hoffmann 和 O’Donnell 的论文的术语,我们也引入了一个概念 $\sum -term$,定义如下:
- 对于所有的 $ i \in \sum$,$rank(i) = 0$,i 是一个 $sum-term$。
- 如果 $ i(t_1, … , t_m) \in \sum $ 其中 $m = rank(i) > 0$,则 $i(t_1, …, t_,m)$ 是一个 $\sum -term$ 提供者。
- 除此之外,其它的都不是 $\sum -term$。
因此,一个树模式是一个$\sum -term$,则允许我们将模式 I 和模式 II 写为 $a(a(v, v), b)$ 和 $a(b, v)$。$\sum -term$ 是有序的 – 如,$a(b, v)$ 是不同于 $a(v, b)$ 的 – 意味着如加法之类的联结操作必须通过模式复制处理,就像在 Glanille-Graham 方法里一样。
我们也介绍如下定义:如果任意包含模式 p 的匹配集都包含另一个 q,则模式 p 被认为是归入到模式 q 里的(写作$p \geq q$。例如,给定两个模式 $a(b, b)$ 和 $a(v, v)$,我们有 $a(b, b) \beq\ a(v, v)$,因为,无论何时 b 节点被匹配上,v 节点显然也会被匹配上。根据这个定义,所有的模式都可以归入自己。一个模式 p 严格地归入另一个模式 q (写为 p > q),当且仅当$p \beq q$ 且 $p \neq q$。最后,一个模式 p 立即归入另一个模式 q(写作 p > i q),当且仅当,不存在其它模式 r 使得 $ p > r $ 且 $ r > q $。为了完备性,如果 p 和 q 的匹配集中没有出现相同的模式,则认为两者是不一致的;如果存在一个树可以匹配 p 但不能匹配 q,且存在另一个树可以匹配 q 但不能匹配 p,则认为两个是独立的。不包含对立模式的模式簇被称为简单模式簇,然后我们的模式簇是简单的,因为不存在一个树可以都匹配上模式 I 和模式 II 两个模式。
为简单模式簇生成查找表
简单模式簇的概念是比较重要的。通常,每张查找表的大小是模式簇大小的指数,生成这些表的时间也是一样的。但是,Hoffmann 和 O’Donnell 确认了简单模式簇的可潜在匹配集的数量是等于模式的数量,每个这样的匹配集可以用一个简单树模式表示 – 即出现在这个匹配集中最大的模式。直观来讲:如果一个模式簇是简单的 – 意味着它缺乏独立的模式 – 则对于任意匹配集合中的每对模式,它必定有一个模式可以归入其它模式。最后,对于每个匹配集,我们可以在该匹配集中出现的模式之间形成包含顺序。例如,假设我们有一个包含 m 个模式的匹配集,我们可以将这些模式排列成$p_1 > p_2 > … > p_m$。因为包含的“最高”次序的模式(即,包含了匹配集中所有的其它模式的模式)只能出现在一个匹配集中 – 否则簇中就出现了两个模式是成对独立的 – 我们可以使用模式的标签表示整个匹配集。同时也要记住的是,沿着表中一个维度的下标也会成为赋给当前节点子孩子的标签,从而成为表达式树的标签。最后,如果我们假设标签 1 和标签 2 分别表示子模式 b 和 $a(v, v)$,则一个有效的查找表 $T_a[1, 2]$ 意味着我们当前站在一个树 t 的树根下,其中最大的可以被匹配上的模式是 $a(b, a(v, v))$,且赋给这个节点的标签是最大模式的标签,可以被 $a(b, a(v, v))$ 归约。如果我们知道包含的顺序,那么我们可以轻松地检索到该模式。
为了找到包含的顺序,我们首先枚举出所有的出现在我们的模式簇里的单独子树。在我们的场景中,这包含了 $v, b, a(v, v), a(b, v)$ 和 $a(a(v, v), b)$,我们将其表示成 S。然后,我们给每个子模式赋一个按顺序的编号,从 0 开始。这些表示可以在模式匹配期间使用的标签,因此它们之前的顺序不是很重要。
下面我们构造 S 的归纳图,表示为 $\overline{G}_S$,其中每个节点 $n_i \in \overline{G}_S$ 表示一个子图 $s_i \in S$,每条直接边 $n_i \to n_j$ 表示 $s_i$ 归入 $s_j$。对于我们的模式集,我们最终得到了图 3.9(c)中所示的包含图,这是我们使用图 3.10(a)中给出的算法产生的。这个算法的基本运行过程如下:一个模式 p 只归入另一个模式 q,当且仅当 p 的根和 q 的根是相同的符号,然后 p 的每个子树归入 q 中相应的子树。为了检查一个树是否可以归入另一个,我们会简单地检查 $\overline{G}_S$ 中的相关节点是否存在一条边。因为任意模式都可以归入自己,我们从添加所有的循环边开始,检查一个模式是否可以归入另一个,如果存在一个则添加一条边,然后一直重复直到 $\overline{S}$ 稳定为止。幸运地是我们可以最小化检查的次数,即通过先把 S 中的子模式按照高度升序排序,然后按顺序比较子模式。一旦我们有了$\overline{G}_S$,通过给$\overline{G}_S$中的节点标记一个拓扑序,我们找到所有模式的归入顺序,对于这个存在着一些已知的方法(拓扑序的定义可以在附录 C 中找到)。
现在我们通过图 3.10(b)概述的算法生成了查找表;在我们的例子中,它给我们的是图 3.9(d)(e)和(f)的表。从一个表从空模式初始化开始,算法增量地更新带有匹配了相关树的下一个大模式的标签条目。因为我们以包含的递增顺序迭代模式,每个条目的最后一次赋值将会是匹配了我们模式簇的最大模式。
总之,因为模式需要被排序,我们需要复制包含了可交换操作的模式,通过交换操作数的子树完成。但是,做这个产生的模式是成对独立的,因此破坏了模式簇的简单属性。这个场景下,本算法也能产生可用的查找表,但是选择只能在包含一个可交换模式的匹配集中进行,没有其它的了(这取决于表生成期间最后使用了 S 中的哪个子模式)。最后,不是所有的匹配集实例都能在模式匹配期间找到,这可能会反过来妨碍到最优的指令选择。
压缩查找表
Chase[49] 开发了一个压缩最后查找表的算法,进一步提高了 Hoffmann 和 O’Donnell 的表生成技术。关键的见解是查找表通常包含冗余信息,因为许多行和列都是重复的。例如,从我们之前的例子中的 $T_a$ 里可以清楚地看到,图 3.11(a)中也提供具体的信息。通过引入一组下标映射,通过映射索引映射表中相同的列或行到查找表中同一列或者同一行,可以删除掉冗余。然后,查找表可以减小到只包含最少量的信息,如图 3.11(b)所示。用 $\tau_a$ 表示$T_a$ 的压缩版本,相关的索引映射是$\mu_{a, 0}$ 和 $mu_{a, 1}$,然后我们通过$T_i[l_0, …, l_m]$ 和 $T_i[\mu_{i,0}[l_0], …, \mu_{i,m}[l_m]]$。
表压缩对于某些模式簇也会有额外的收益,查找表可能是很庞大的,甚至可能一开始就无法构造出来。幸运地是,Chase 发现了它们可以在生成的时候就被压缩掉,从而突破了可以生成多大的查找表的限制。Cai 等人 [40] 提高了 Chase 的算法的渐进复杂度边界。
动态规划的最优模式选择
一旦可以在线性时间内找到整个表达式树的所有可能匹配集后,解决线性时间内最优模式选择问题的技术也开始出现了。根据资料,Ripken [216] 是第一篇提出最佳指令选择的可行方法的论文,它是 1977 年的技术报告给出的。Ripken 的方法是基于 Aho 和 Johnson 的动态规划算法 – 在第一章中有提到 – 然后扩展它来处理有多种寄存器类型和地址模式的实际指令集。为了简洁起见,今后我们会将动态规划简称为 DP。
尽管 Ripken 似乎是第一个提出基于 DP 的最优指令选择器设计的人,但它仅是一个提议。第一次对这种系统进行实际尝试的是 Aho 等人[6, 7, 245]。
TWIG
在 1985 年 Aho 和 Ganapathi 给出了一个称为 CGL (代码生成器语言)的语言,它里面是通过属性语法描述(见图 3.12 的例子)树模式的,然后由 TWIG 编译器生成器处理。就像 Ripken,生成的指令选择器选择最优模式集是用的 Aho 和 Johnson DP 算法的一个版本,在表达式树上进行遍历:一遍自顶向下,跟着是一遍自底向上,最后是另一遍自顶向下。在第一遍里,使用 Aho-Corasick 字符串匹配算法的一种实现找到所有的匹配集[5]。第二遍应用 DP 算法选择模式,然后最后一遍输出相关的汇编代码。我们继续研究 DP 算法,因为我们已经对如何做树模式匹配相当熟悉了。
图 3.13 简单地概述了 DP 算法。对于表达式中的每个节点,我们维护一个数据结构,记录将节点归约到特定非终结符所需的最低成本,以及可以进行这个归约的规则。记住在匹配集中找到一个模式,对应于出现在指令集语法(3.3 节讨论过的)中的一个产生式的右侧。应用一条规则的成本是规则本身的成本加上使用这条规则归约子节点到任意非终结符的成本之和。因此,成本是单调递增的。也可能发生不只是一条规则被应用到当前节点上,也可能是多条。当语法包含链式规则的时候就会出现这种情况,这种规则的产生式的右侧由单个非终结符组成。例如,一个终结符 A 到 c 的产生式可以通过 $ c \to A $ 完成,也可以通过一系列的规则调用完成,如:
$$
\begin{align}
b& \to A \
b&^{‘} \to b\
c& \to b^{‘}
\end{align}
$$
因此,算法必须获取这些链式规则,并在所有依赖于它们的规则之前检查它们。这称为计算传递闭包。
当已经计算好根节点的成本,则我们可以选择最廉价的规则集,从而将整个表达式树归约到期望的非终结符上。图 3.14 概述了选择算法:对于一个给定的目标,由非终结符表示的,选择最廉价的可用的规则来归约当前的节点。然后为出现在被选中的规则右边的非终结符做相同的事,从而变成相关子树的目标。这个算法也可以正确地应用到链式规则上,和应用到一条规则上一样,从而可以以不同的目标在同一个节点上调用 SELECTANDEMIT。但是,需要注意的是,由于模式可以任意大,因此必须采取措施来选择正确的子树,它可以出现在表达式树里当前节点的位置到往下几个层级。
DP 对 LR 解析
比起基于 LR 解析的方案,DP 方案具有几个优势。首先,归约冲突由成本计算算法自动处理了,因此移除了 LR 解析需要的规则排序,它会影响 LR 解析的代码质量。第二,会导致 LR 解析卡在无限循环的规则循环不在需要显式地打破。第三,机器描述可以做得更简洁,因为只有成本不同的规则可以合并到一条单一规则上;再次使用 VAX 机器作为例子,Aho 等人表示只需要使用 115 条规则就可以实现整个 TWIG 规范,它是使用 Ganapathi 和 Fischer 的基于属性指令集语法支持相同机器的一半大小。
但是,该方法要求代码生成问题具有最优子结构的性质 – 即,通过解决每个最优子问题可以生成最优的代码。这种场景不是经常存在的,因为有些模式集的总和是大于另一些被选择模式的,但它们实际却可以生成更好的汇编代码。例如,让我们假设我们需要选择模式来实现一组可以相互独立执行的操作。指令集提供了两个选择:要么使用两条机器指令,每条花费 2 个周期;或者只使用一条 3 周期的指令。如果第一个选择中的两条指令是顺序地执行则第二个选择更有效。但是,如果指令调度能够并行化这些指令,则第一个选择更好。这进一步突出了孤立地考虑最佳指令选择的问题,如我们在第一章讨论的。
进一步实现
TWIG 后续的几个提升是由 Yates 和 Schwartz[267] ,还有 Emmelmann 等人[79] 完成的。Yates 和 Schwartz 通过将 TWIG 的自顶向下方法替换为 Hoffmann 和 O‘Donnell 提出的更快的自底向上算法,以及扩展属性来支持更强的谓词,提高了模式匹配率。Emmelmann 等人修改了运行的 DP 算法,使其可以在前端构建 IR 树时运行,并且前端也将辅组函数的代码直接内联进 DP 算法来降低固有开销。Emmelmann 等人在称为 BEG 的系统中实现了他们的改进方案(后端生成器),这个修改版本当前应用于 CoSy 编译器中[23]。
Fraser 等人 [104] 在称为 IBURG 的系统中做了相似的改进,变得比 TWIG 更简单且更快 – 比起 TWIG 3000 行的 C 代码,IBURG 只需要 950 行代码,并以 25 倍的速度生成质量相当的汇编代码 – 已经被应用到几个编译器中(如,RECORD [174,184],和 REDACO[162])。Gough 和 Ledermann [124,125] 后面在一个名为 MBURG 的实现中对 IBURG 进行了一些小的改进。IBURG 和 MBURG 都被用不同的编程语言重新实现过,如基于 Java 的 JBURG [243],和用 C– 实现的 OCAMLBURG [246]。
根据 [42, 173],Tjiang [244] 后来将 TWIG 和 IURG 的想法整合进了一个新的实现称为 OLIVE – 这个名字是 TWIG 的一种副产品 – 做了一些额外的改进,如允许规则使用任意的成本函数而不是固定的,数值类的值。这允许指令选择有更多的功能,如可以通过设置无限的成本使得可以让规则动态的失效,这可以通过上下文进行控制。OLIVE 被用于 SPAM [247] 的实现中 – 一个定点的 DSP 编译器 – Araujo 和 Malik [16] 在尝试将指令选择和调度以及寄存器分配三者相结合的尝试中使用了它。
使用离线成本分析进行更快的模式选择
在刚才讨论过的动态规划方法中,可以动态地计算选择一个模式需要的规则成本,只要规则匹配是完全表驱动的。后来发现可以提前进行它的这些计算,然后以表的形式进行表示,因此可以在模式匹配的时候提高模式选择的速度。我们将这种方式称为离线成本分析,它意味着成本计算可以提前到生成编译器的时候进行,而不用在输入程序编译的时候进行。
扩展匹配集标签带上成本
为了可以用离线成本分析,我们需要扩展标签,让其不但可以表示匹配集,也有模式在特定目标下达成最小覆盖成本需要的信息。为了区分这两个,我们将扩展后的标签形式称为状态。一个状态本质上是目标,模式和成本三者的特定组合的一个表示,其中每个可能的目标 g 被关联到一个模式p 和一个相关的成本c。这个上下文中的目标通常决定了一个表达式的结果必须出现的地方(如,一个特定的寄存器类型,或内存等),而在语法术语中它意味着每个非终结符被关联到一条规则和一个成本上。这种组合使得:
- 对于任意表达式,它们的根节点都被标记了一个特定的状态;
- 如果根节点的目标必须是 g,
- 则通过在根节点选择模式p,整个表达式树可以以最小的成本进行覆盖。与目标是其它的相比,这个覆盖的相对成本是等于 c 的。
理解这里的一个关键点是,一个状态并不一定需要携带如何最优化覆盖整个表达式树的信息,实际上如果这样子尝试的话,将需要无数的状态。而是状态只需要表示足够的关于如何覆盖可以出现在任意表达式树的不同关键形状的信息即可。为了进一步解释这个,让我们观察大部分(如果不是全部)目标架构是如何操作的:在两条机器指令执行期间,数据是通过存到寄存器或者存到内存进行同步的。数据出现在特定位置的方式通常不影响之后的机器指令的执行。因此,根据可用的机器指令,通常可以在某个关键的地方断掉表达式树,且不影响代码指令。这会产生有许多更小的表达式树的森林,每个在根上都有特定的目标,然后它们可以独立地最优覆盖。换句话说,状态集只需要能共同表示表达式树可以做的所有分割的所需的信息即可。当然,表达式树并不需要在模式选择之前就真的切分成小块了,但按这种方式来考虑它,可以帮助我们理解为什么我们通过有限的状态就能获取最优的模式选择。
因为一个状态是一个标签的简单扩展形式,用状态标记表达式的过程与之前(见 39 页的图 3.8)完全一样,因为我们只需要替换查找表。然后,就像图 3.15 一样完成模式选择和代码生成,它或多或少与结合动态规划的算法是相同的(与第 45 页的图 3.14 相比)。但是,我们还没有描述如何计算这些状态。
第一个应用离线成本分析的技术
根据 [26],模式选择进行离线成本分析的想法第一次是由 Herry [138] 1984 年的博士论文引入的,然后 Hatcher 和 Christopher [134] 是第一个尝试实际应用它的。但是,这种方法似乎不太为人所知,因为很少有文献引用它。
他们 1986 论文描述,Hatcher 和 Christopher 的方法是 Hoffmann 和 O‘Donnell 工作的扩展。直观上是要找可以应用到某些表达式树的哪些规则,这些表达式树的根节点已经赋了一个标签l,这样子整个表达式树可以以最低成本规约到一个给定的非终结符上 nt。Hatcher 和 Christopher 认为最优的模式选择,我们可以考虑每一对标签 l 和非终结符 nt,然后总是应用可以规约最大表达式树 $T_i$ 的规则,这就表示l以最低的成本变成了 nt。在 Hoffmann 和 O’Donnell 的设计中,只有一个空的符号可以匹配任意的子树,$T_l$ 等于匹配集中出现的最大模式,但是为了适配指令集语法,Hatcher 和 Christopher 的版本每个非终结符都包含一个空。这意味着不得不遍历匹配集中出现的所有模式才能找到 $T_l$。然后,我们为了每一对模式,计算将一个较大模式 p 转换到一个可包含的,更小的模式 q(即,p > q)需要的成本。这个成本通过使用其它模式递归地重写 p 直到它等于 q,它最后会被标注到包含图中,让这个转换成本等于所有应用到的模式的和。我们用函数 $reducecost( p \to^{}) q$。根据这个信息,我们通过找到规则 r,来找回将 $T_l$ 的最低成本归约变成目标 g 的规则
$$
reducecost(T_l \to^{} g) = reducecost(T_l \to^{*} tree\ pattern\ of\ r) + cost\ of\ r.
$$
这要么选出 l 匹配集出现的最大模式,要么存在与其它模式组合的具有较低成本的较小的模式。虽然我们添加了许多的注解,但主要思想还是来自 Hatcher 和 Chritopher 的方法。
通过将已选择的规则编码到一张额外的表供模式选择期间查询,我们构造了一个完整的表驱动指令选择器,它同时也执行最优的模式选择。Hatcher 和 Christopher 也增强了算法可以检索匹配集,从而包含具有交叉操作的重复模式,然后可以从一些匹配集中省略它们。但是如果存在完全独立的模式,则 Hatcher 和 Christopher 的设计并不总是保证表达式树可以最优地覆盖完。此外,还不清楚代表标签的最大表达式树的最优模式选择是否是所有表达式树的最优模式选择的精确近似。
使用 BURS 理论生成状态
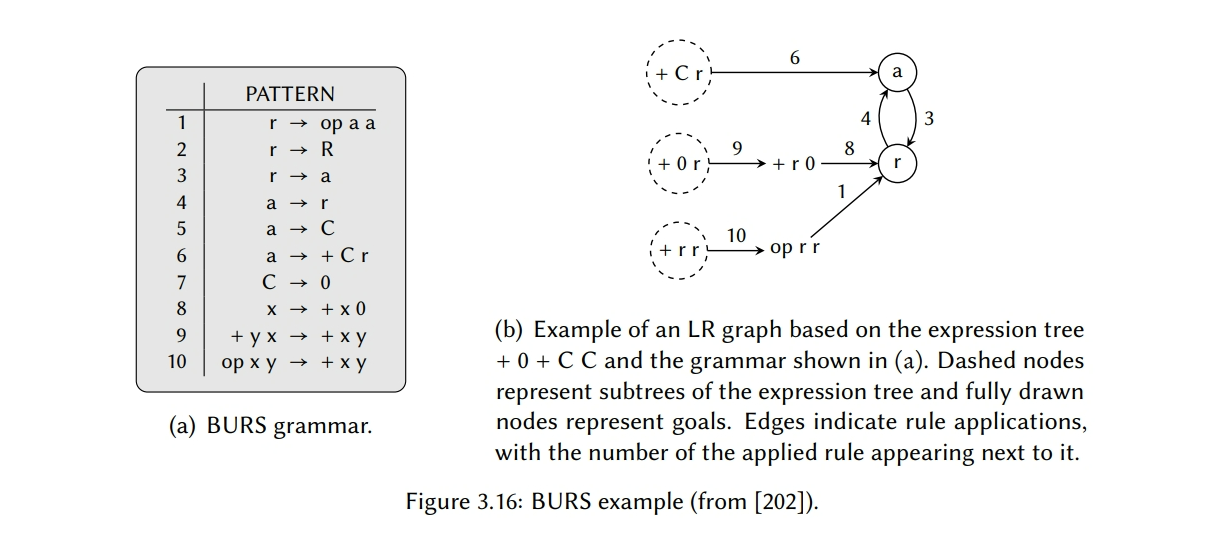
一个不同的更广为人知的生成状态的方法是 Pelegri-Llopart 和 Graham [202] 开发的。在他们重要的 1988 年论文中,Pelegri-Llopart 和 Graham 证明了树重写的方法总是可以让所有的重写发生在树的叶子节点上,因此产生了自底向上重写系统(简称 BURS)。我们将这样的规则集称为BURS语法,它们类似于之前已经见过的语法,除了 BURS 语法允许多符号 – 包括终结符 – 出现在生成式的右边。图 3.16(a)给出了这种语法的一个例子,Dold 等人[71,273]后面用抽象状态机开发了一个方法来证明 BURS 语法的正确性。
使用这个理论,Pelegri-Llopart 和 Graham 基于给定的 BURS 语法开发了一个算法,用于计算最优模式选择所需的表。方法如下:对于一个给定的表达式树 E,和一条边,它表明特定重写规则在子树上的应用。图 3.16(b)给出了一个这种图的例子。设定一些节点作为目标(即,树重写期望的规则),然后从 LR 图中选出一个子图称为唯一不可逆 LR 图(UI LR),这样子重写的可能性是最小的。寻找 UI LR 图是一个 NP-完全的问题,因此 Pelegri-Llopart 和 Graham 应用一个启发式,迭代地移除被视为是“有用的”的节点。然后每个 UI LR 对应一个状态,通过为所有可以作为输入的可能的表达式树生成相应的 LR 图,我们可以找到所有必须的状态。
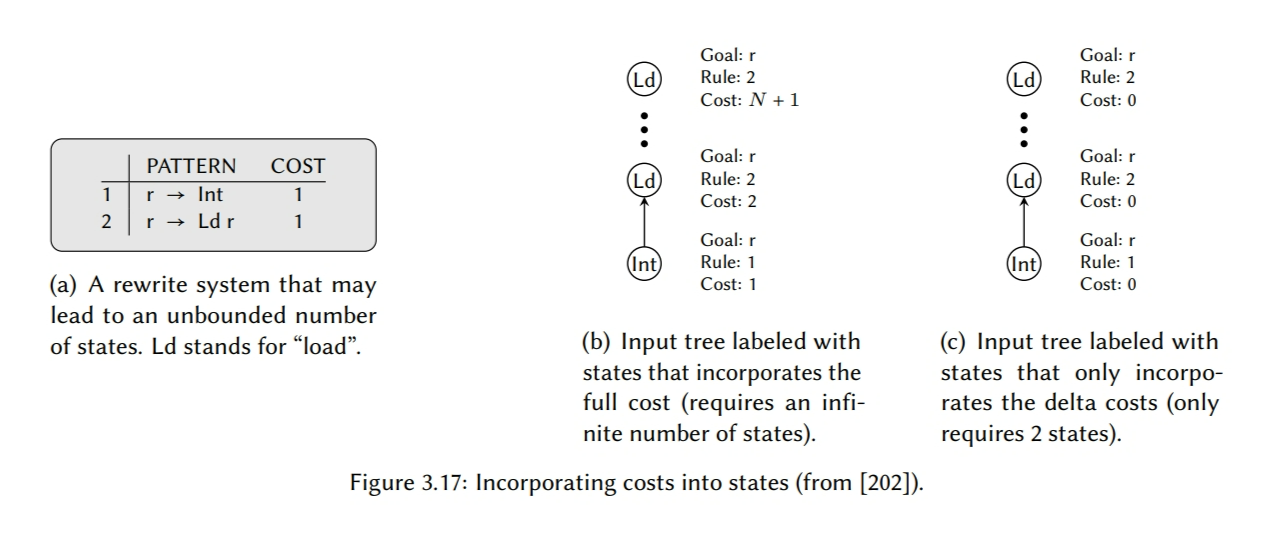
实现有限数量的状态
为了获取最优的模式选择,增强了LR图,每个节点不在是表示一个树模式,而是一个$(p,c)$对,其中$c$表示到达模式$p$的最小成本。正如我们之前讨论的那样,这些就是各个状态所体现的信息。一个朴素的方法是将到达一个特定状态的全成本包含在状态里,但是这依赖于重写系统,它可能需要无限的状态数量。图3.17(b)给出了一个这样的例子。一个更好的方法是考量所选模式的相对成本。通过计算c作为p的成本和LR图中可以出现的任意模式中最小成本之间的差值来获得这个相对成本。这样可以产生相同的最优模式选择,但是只需要固定数量的状态,如图3.17(c)所示。这个成本称为$delta$成本,因此增强的LR图被称为$\delta-LR$图。在生成$\delta-LR$图的时候,为了限制数据大小,Pelegrí-Llopart和Graham使用了扩展版的Chase表压缩算法【49】,我们在43页讨论过它了。
在测试期间,Pelegrí-Llopart和Graham汇报了他们的实现产生的状态表只比LR解析产生的稍微大了一点,生成的汇编质量与TWIG的相当,但是速度快了5倍多。
BURS 不等于离线分析
因为它发表之后,许多后续的论文错误地将离线成本分析与BURS关联起来,通常使用的术语是BURS states,但实际上它们两者是相互独立的。虽然Pelegrí-Llopart和Graham的工作确实让离线成本分析成为现代指令选择既定的一部分,但BURS理论的应用只是意味着使用表获得最优模式选择。
在Pelegrí-Llopart和Graham引入BURS不久之后,Balachandran等人【26】在1990年发表了一篇论文,描述了生成状态的另一种方法,它更简单和高效。他们算法的核心是使用那些已经提交的状态来创建新的状态以出现在状态表上。需要记住的是,每个状态表示非终结符,规则,和成本的结合,其中成本已经规范化了,因此状态里每条规则的最低成本是0。如果为所有非终结符和成本选择的规则相同,则两个状态是相同。当创建了一个新的状态,会检查它是否被见过 – 如果是则丢弃它,否则将它添加到已提交的状态集里 – 这个过程会一直重复直到不在创建新的状态。稍后我们会更详细地介绍。
比起 Pelegrí-Llopart和Graham的算法,这个算法复杂度更低也更快,因为它直接生成最小状态集,替代了先枚举所有可能的状态在化简它们。此外,Balachandran等人将机器指令表示为更加传统的指令集语法 – 与Glanville-Graham方法里使用的 – 而不是BURS语法。
线性语法
在同一篇论文里,Balachandran等人也介绍了线性语法的思想,它意味着语法里出现的每个产生式的右侧都被限制为下面的情况之一:
- $lhs \rightarrow Op\ n_1\ … n_k$:Op是一个终结符,表示一个操作符,其$rank(k) > 0$,$n_i$是所有的非终结符。这些称为基础规则。
- $lhs \rightarrow T$:T是一个终结符。它也是一个基础规则。
- $lhs\rightarrow nt$:nt 是一个非终结符。这些称为链式规则。
一个非线性语法可以简单地重写为线性形式,只要产生所需的转换,引入新的非终结符和规则,如:

这种语法的优势是模式匹配的问题会被简化成树模式上的根节点的操作和表达式树上节点的操作的比较。这也意味着出现在规则里的产生式变得更均匀,这极大地简化了状态生成任务。
生成状态表的一个更简单的工作队列方法
Proebsting【207,208】提出了另一个状态生成算法,类似于Balachandran等人的。它也被Fraser等人【105】实现在一个称为BURG的知名代码生成系统里,自从这个系统在1992年发表之后,在编译器社区里引发了命名约定,我选择将其称为Burger现象。虽然Balachandran等人的是第一个,但是我们继续研究Proebsting算法,因为它更好地文档化了。
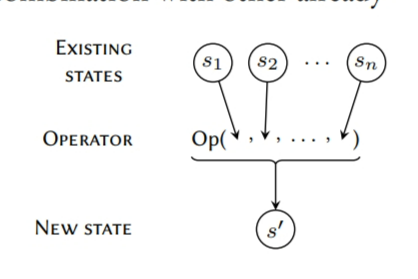
这个算法是围绕着一个工作队列展开的,它包含了正在考量的状态储备。和Balachandran等人的一样,它假设了指令集语法是线性形式的。这个队列首先初始化为从所有可能的左侧叶子节点产生的状态。然后,从队列里弹出一个状态,用于尝试于其它已经访问过的节点进行合并来产生新的节点。它通过有效地模拟出现下面的节点会发生的情况来完成的,如果这一组节点作为一些操作符符号的子节点出现,被一些已经合并的节点包括刚被弹出来的节点标记了:如果操作符节点可以被已经存在的状态标记则没有事情发生;如果没有则创建新的节点,保证所有的可用链式规则都被应用到这个状态,因为它们会影响到成本,然后将其放入队列中。对于每个可能的状态合并和操作符符号都会做检查,当队列为空的时候算法就会结束,这表明指令集语法所必须的所有状态都已经生成了。
进一步提升
如果已提交状态的数量是最小的,则生成状态表所需要的时间也可以被降低。根据【207】,它是第一个做这个的,是由Henry完成的,后来由Proebsting【207,208】进一步提升和通用化。Proebsting开发了两个方法用于降低已生成状态的数量:状态裁剪,它扩展和通用化了Henry的想法;一个称为链式规则裁剪的新技术。不深入的探究,状态剪枝通过删除那些被证明不会成为最低成本覆盖一部分的非终端节点,增加了两个已创建节点相同的概率。然后链式规则剪枝通过尽可能地使用相同规则进一步最小化状态的数量。这个技术后来被Kang和Choe【17,148】改进了,他们利用通用机器描述的属性降低冗余状态测试的数量。
更多应用
将模式选择扩展成带有离线成本分析的方法已经被应用到多个编译器相关的系统中了。一些需要关注但我们还没有提到的应用有:UNH-CODEGEN【136】,DCG【83】,LBURG【132】,和WBURG【209】.BURG也有一个Haskell版本称为HBURG【240】,它被Boulytchev【32】用于辅助指令集选择,LBURG用于LCC(Little C compiler)【132】也被Brandner等人用于开发一种架构描述语言,这种语言的机器指令可以被自动推导出来。
延迟状态表生成
获得最有模式选择有两个主要的方法–一种是在输入程序编译时动态计算成本,另一种是依赖于通过状态表的静态计算–两者都有它们各自的优劣势。前者的优点是能够支持动态成本计算,即一个模式的成本依赖于上下文而不会保持静态,但是它也比纯粹的表驱动慢很多。而后一个技术倾向于生成更大的指令选择器,因为使用了状态表,它的生成是非常耗时的 – 对于病理性语法是不可用的–并且它们只支持成本是固定的语法规则。
最佳状态表和DP的结合
在2006年,Ertl等人【86】开发了一个方法,其允许延迟和按需生成状态表。直观上,与其提前为所有可能的表达树生成状态,可以只生成实际出现在输入程序中的表达树所需的状态。
该方法简单概述为:当指令选择器遍历一个表达式树的时候,使用动态规划创建覆盖它的子树所需的状态。一旦生成了状态子树就被标记了,并且使用相似的表驱动技术选择模式。然后,如果有相同的子树出现在其它位置–在相同的表达式树或者输入程序的另一个表达式树–相同的状态会被重复利用。这允许分摊状态生成的成本,因为与使用纯粹基于DP的模式选择器处理子树的方法相比,它可以更快速地最优化覆盖。Ertl等人汇报说比起纯粹的表驱动实现,状态重用的固有开销是最小的,第一次计算状态然后标记表达式树的时间和使用原始基于DP方法选择模式的时间是不相上下的。此外,通过延迟生成状态,可以处理更大和更复杂的指令集语法,不然所需的状态数是不可估计的。
Ertl等人也扩展了这个方法来处理动态成本,只要根节点的成本不同,就重新计算状态并存储到哈希表中。作者说这边会出现一个额外的开销,但是与纯粹的基于DP的指令选择器相比仍然执行得更快。
树覆盖得其它技术
到目前为止,我们在本章中讨论过的传统树覆盖方法有:LR解析,自顶向下递归,动态规划,和使用状态表。这一节中,我们会了解其它技术,这些技术也是基于上述原理的,但是使用了更加非正统的方法解决它。
基于形式化的方法
导数的同态和反转
Giegerich和Schmal【120】在1988年的论文中提出了一个代数框架,它的目标是允许代码生成的所有方面–即,不但有指令选择而且有指令调度和寄存器分配–可以被形式化地描述,从而简化机器描述和使能形式化验证。简单来说,Giegerich和Schmal将指令选择的问题重新描述为“层次导数的问题”,它本质上是一个机制的规范和实现机制: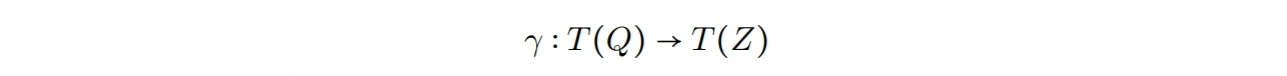
其中,$T(Q)$和$T(Z)$表示一个代数术语,它们是为了表达各自的中间目标机器语言。因此,$\gamma$可以被视为生成指令选择器。然而,机器描述通常包含$Z$中每条机器指令被表示成Q的规则。因此,我们将机器规范视为一个同态,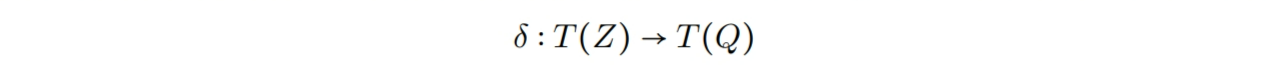
然后指令选择生成器的任务就是通过反转$\delta$推导出$ \gamma $。通常这个是通过模式匹配实现的。为了最优指令选择,每当某个$q\in\ T(Q)$具有多个 $z\in\ T(Z)$使得$\delta(q) = z$,生成器必须将$\delta$的反转构造和一个选择函数$\xi$交织在一起。理论上,这个给予我们如下的功能函数: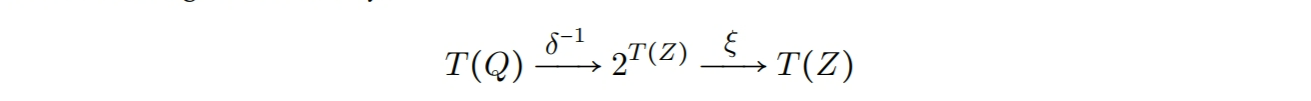
在同一篇论文里,Giegerich和Schmal也证明了如何使用此框架表达其它的方式,如树解析。随后Despland等人提出【66,67】一个相似的方法,基于重写技术的,它的实现称为PAGODE【41】。读者如果对更多细节感兴趣建议参考引用论文。
方程式逻辑
在1991年,Hatcher【135】开发了一个类似于Pelegrí-Llopart和Graham的方法,但它依赖的不是BURS理论的而是方程式逻辑【199】。这两者密切相关,因为他们都应用了一组预定义规则–即,从机器指令中得出的那些与公理变换相结合–来将一个输入程序改写成一个单目标术语。但是,在方程式规范中是有优势的,它所有的规则都是基于一组内置操作,在代码发射的时候,它们每个都有一个成本和语法表示。然后每条规则的成本都等于所有应用到这条规则的内置操作的成本之和,因此移除了手动设置的过程。此外,不需要预定义内置操作,而是作为方程式规范的一部分给出,作为一个非常通用化的机制用于描述目标机器。有个实验结果来自选择问题,它有个称为UGC的实现–论文没有说明这个缩写的含义–这个结果表明和同时代技术相比,它可以在更短的时间里生成质量相当的汇编代码。
树状态机和串联传感器
在相同的方式下,Glanville-Graham的方法采用了派生自语法解析的技术, 而Ferdinand等人【94】认识到有限树状态机【117】的成熟理论可以用于解决指令选择问题。在1994年的论文里,Ferdinand等人描述了使用树状态机是如何解决模式匹配和模式选择的问题的–有和没有最优的场景都可以,也给出了他们采用的生成算法和状态机。一个实验性的实现证明了这个方法的可行性,但是结果没有和其它技术进行比较。后来,Borchardt【31】提出了类似的设计,他使用树串联传感器【81】替代树状态机。
重写策略
在2002年,Bravenboer和Visser提出了一个适用于指令选择的设计,它是基于规则的程序转换系统【252】。虽然系统称为STRATEGO【253】,但是机器描述可以通过包含模式选择器本身进行增强,从而允许它根据目标机器的特定指令集进行增强。Bravenboer和Visser将其称为提供一个重写策略,并且他们的系统允许建模多个策略,如穷举搜索,最大匹配和动态规划。但是,显然不支持纯粹的表驱动技术,因此,排除了应用离线成本分析的可能性。Bravenboer和Visser认为这个设置允许合并多个模式选择,但是他们的论文里没有给出有收益的例子。
遗传算法
Shu等人应用遗传算法(GA)【122,219】的理论–它尝试模拟自然演进的过程–来解决模式选择问题。1996年的论文描述了,将解决方案拟定为一个DNA链–称为染色体–然后为了最终得到更好的解决方案,拆分,合并,和变异它们。对于一个给定的表达式树–它的匹配集已经通过一个$O(nm)$的模式匹配器找到了–Shu等人将每条染色体表示为一个二进制位串,其中1表示一个特定模式被选择了。类似的,0表示一个模式没有被用于树覆盖。因此,一条染色体的长度等于所有匹配集中出现的模式数量之和。然后,目标就是寻找最大化匹配函数f的染色体,Shu等人将f定义为
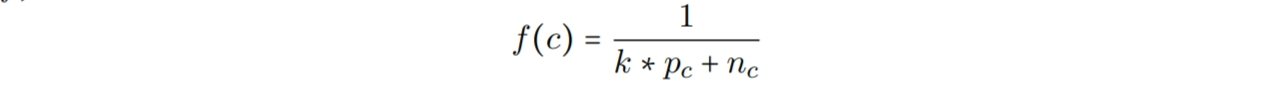
其中,$k$是大于1的可变常量,$p_c$是染色体$c$中可选择的模式数量,$n_c$是$c$中节点数量,这些节点被多个模式覆盖。首先,固定数量的染色体被随机生成和进化。最好的一个会被保留,并提交一个标准的GA操作,如适应度比例重生成,单点杂交,和单点变换,使之可以产生新的染色体。然后一直重复这个过程直到达成一些终结准则。当将这个算法应用到中等大小的表达式树(最多50个节点),作者宣称可以在“可接受的”时间里找到最优的树覆盖。
格图
在本章我们最后调研的一个方法是Wess【259,260】的,这是个基本没有被使用的方法。对于数字信号处理器这种特定的转换目标,Wess的设计通过使用格图的方式将指令选择和寄存器分配整合在一起。
一个格图是一种每个节点都是由最优值数组(OVA)组成的图。OVA中的每个元素表示数据要么被存储到内存(m),要么被存储到一个特定的寄存器($r_x$),并且它的值表示从叶子节点到这个节点的最低累积成本。这个的计算类似于动态规划技术。如果数据被存储到一个寄存器中,OVA元素也表示这个操作的其它可用寄存器。例如,一个目标机器有两个寄存器–$r_1$和$r_2$–则生成的OVA如下:
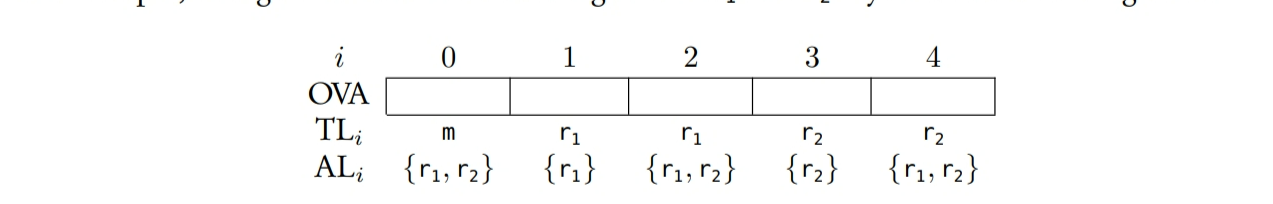
其中$TL_i$表示数据的目标位置,$AL_i$表示可用的位置。
我们使用如下的方法创建格图。对于表达式树中的每个节点,一个新的节点表示一个OVA被添加到格图。为了处理输入值在使用之前需要先被转换到另一个位置的场景(当这个输入值被放入到内存时,就需要这种),需要给作为表达式树叶子的节点添加两个格图节点。现在让我们将$e(i,n)$表示为节点$n$的OVA元素$i$。对于一元操作节点,如果存在一条指令使用了$m$中的$j$表示的位置里存储的值,执行$n$的操作,并存储结果到$i$表示的位置,则在$e(i,n)$和$e(j,m)$之间添加一条边。类似的,对于一个二元操作节点$o$,如果存在一条相关的指令将结果存储到$k$,则从$e(i,n)$和$e(j,m)$到$e(k,o)$之间画两条边。以此类推,可以扩展到n维操作,图3.18给出了一个完整的例子。
因此,格图里的边对应一个机器指令和寄存器分配可能的组合,通过表达式树一个特定的操作实现,格图中每个叶子节点到它的根节点的路径表示这种组合的一个选择,它的集合实现了整个表达式树。通过记录成本变化,选择具有最小成本且以格图根节点的OVA元素为结尾的路径,我们可以获得最优的指令序列。
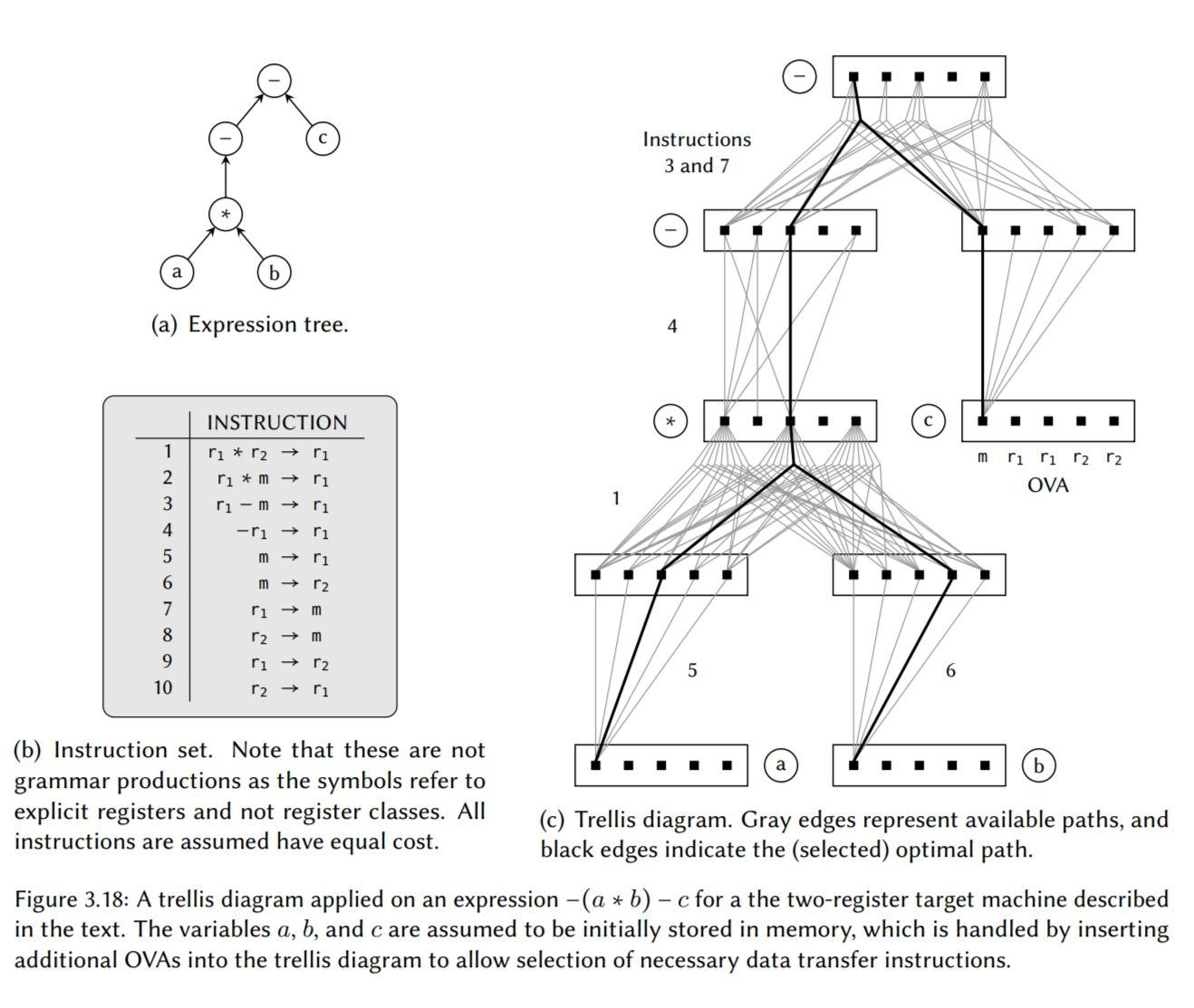
Wess方法的优势是带有异构寄存器的机器(即,访问不同的寄存器需要不同的指令)更容易被处理,因为指令选择和寄存器分配几乎是同时完成的。但是,格图中的节点数量是寄存器数量的指数级。Fröhlich等人改善了这个问题【108】,他们扩展了算法,以延迟的方式构建格图。但是,为了效率,这种方法需要表达式节点和机器指令之间一一映射。
总结
在本章中,我们研究了基于树覆盖原则的多个算法。与宏覆盖相比,这些方法允许使用更复杂的模式,从而可以产生更高效的指令选择器;通过应用动态规划算法,可以在线性时间里产生最优代码。一些方法也将离线成本分析结合到表生成器中,进一步加速了代码生成。换句话说,这些方法非常的快速且高效,同时可以支持广泛的目标机器。因此,树覆盖变成了最知名的–即使不在是最多应用的–指令选择原理。但是,将本身限制为树,也带来了几个固有的缺陷。
树带有的限制
表达式建模不得不带有的第一个限制是:由于树的定义,通用子表达式无法完全在表达式树中建模。例如,如果没有使用如下的解决方法,内联代码是无法直接建模的:
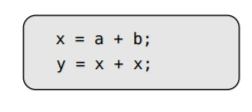
重复共享节点,其波兰式的结果为
1
= y++ab+ab
将表达式拆分为森林,结果为
1
2= x + ab
= y + xx第一个技术会导致汇编代码里产生额外的机器指令,而第二个方法妨碍了复杂指令的使用;两个方法的代码质量都是有妥协的。
因为树只允许单根节点,多输出的机器指令无法被表示为树模式,这是因为指令需要多个根节点。因此,有一些功能–许多指令集都会包含设置条件标志的指令的功能–在指令选择期间无法表示出来。即使那些可以被单操作建模成一棵树的多输出指令也无法被选择,因为指令选择器一次只能考虑一个单树模式。
另一个缺点是表达式树无法建模控制流。例如,一个for语句需要一条基本块间的循环边,这违反了树的定义。因为这个原因,基于树的指令选择器的范围被限制为一次只能为一个表达式树选择指令,所以控制流的代码生成使用了分离模块进行处理。这反过来也将内循环指令的匹配和选择排除在外,这种指令的行为包含了多种控制流。
总的来说,虽然树覆盖原理相比纯的宏展开原理(即,忽略了窥孔优化)极大地提高了代码质量,但是树的固有约束也限制了大多数目标机器提供的机器指令的充分利用。在下一章中,我们将会寻找更通用的原理,可以解决上述部分问题。
DAG 覆盖
就像我们在前一章节见到的,树匹配的原理带有一些缺点:无法合适地表达公用子表达式,且无法建模许多机器特性如多输出指令。因为这些限制是由于完全依赖树结构导致的,我们可以通过将树覆盖扩展到 DAG 覆盖来放开它们。
原理
如果我们移除树中的每对节点都必须只能有一条路径,我们会获得一个新的图形称为有向无环图,通常称为 DAGs。则现在的节点允许有多个输出边,因此表达式的中间值可以在相同的图里共享和重复使用,也会包含多个根节点。为了区分表达式的树建模和 DAG 建模,我们称后者为 表达式 DAGs。一旦能构成这种形式后,指令选择的过程就可以应用我们从前一章学到的模式匹配和模式选择的相同原则来处理。当模式允许多个根节点,我们可以建模和利用大的机器指令集,例如多输出的指令,像 divmod 其可以同时计算商和余数。
DAGs 上的最优模式选择是 NP 完全问题
不幸地是,DAGs 给我们的这种普遍性收益和建模能力的成本是复杂性的的大幅提升。在树上选择一个最优的模式集是可以在线性时间里完成的,但在 DAGs 做相同的事情确是一个 NP 完全的问题。Bruno 、 Sethi [38] 和 Aho 等人[4] 在 1976 年已经证明了这个问题,虽然两者都更关心指令调度和寄存器分配的最优性。在 1995 年,Proebsting [206] 给出了最优指令选择的简洁证明,后来在 2008 年 Koes 和 Goldstein [161] 重新形式化了它。我们会在本文中描述 Koes 和 Goldstein 的证明。请注意完成这个是不需要涉及模式匹配任务的 – 就像我们会看到的,如果模式由树组成,则可以在多项式的时间里完成这个。
证明
这个思路是将 SAT(布尔可满足性)问题精简为一个最优(即,最低开销)DAG 覆盖问题。SAT 问题用来判断一个合取范式(CNF)中的布尔公式是否可以被满足。一个 CNF 表达式是如下形式的公式
$$
(x_{11}\vee x_{12} \vee …) \wedge (x_{21} \vee x_{22} \vee …) \wedge …
$$
变量 $x$ 可以通过 $\neg x$ 取反。因为这个问题已经被证明是 NP-完全的了[62],所有 SAT 可以多项式时间归约成的问题$\chi$,都会使得 $\chi$ 是 NP-完全的。
将 SAT 建模为覆盖问题
首先我们将一个 SAT 问题实例 $S$ 转换为 DAG。直观上,如果我们可以用单元开销的模式覆盖 DAG,则总开销等于节点的数量(假设每个变量和操作都产生一个新节点),那么存在对变量的真值赋值式,公式对其求值为 $T$。因为这个目的,DAG 中的节点可以是 ${ \vee, \wedge,\neg,v, \square, \diamond }$ 类型。我们定义 $type(n)$ 作为节点 $n$ 的类型。分别称 $\Box$ 类型的节点和 $\diamond$ 类型的节点为box 节点 和stop 节点。我们也定义了$children(n)$ 作为 $n$ 的子节点集。对于每个布尔变量 $x \in S$ ,我们创建两个节点 $n_1$ 和 $n_2$,则 $type(n_1) = v$ ,$type(n_2) = \square$,且有一条直连边 $n_1 \rightarrow n_2$。我们对每个二元布尔操作符 $op \in S$ 都做相同的操作,创建两个节点 $n_{1}^{‘}$ 和 $n_{2}^{‘}$,则 $type(n_{1}^{‘}) = op$ ,$type(n_{2}^{‘}) = \square$,且有一条直连边 $n_{1}^{‘} \rightarrow n_{2}^{‘}$。我们通过操作数的箱子节点,将操作符与它的输入操作数 $x$ 和 $y$ 连接在一起,即两条边 $n_x \rightarrow n_{1}^{‘}$ 和 $n_y \rightarrow n_{1}^{‘}$ 其中$type(n_x) = type(n_y) = \Box$。对于一元操作 $\neg$, 我们显然只需要一条这样的边,并且因为布尔 or 和 and 是可交换的,所以边排布的顺序与相关操作符节点的顺序是无关紧要的。最后,只有 box 节点会多于一条输出边。
通过简单地遍历布尔公式,我们可以在线性时间里构造 DAG。图 4.1(b)给出了一个 SAT 问题转换为 DAG 覆盖问题的例子。
布尔操作作为模式
然后我们构造一组树模式 $P_{SAT}$, 它允许我们去推断如何设置 S 中的变量,从而可以满足表达式(见图 4.1(a))。如果值假定被设置为 $T$(true),则模式的形成会有一个 box 节点作为叶子。而且,如果操作的结果判定为 F(false),则模式会有一个 box 节点作为根。确定它的一个方式是,如果模式中的一个操作符消费一个 box 节点,则值必须设置为T;然后如果操作符产生了一个 box 节点,则结果必须设定为F。为了强制整个表达式求值为T,唯一个包含 stop 节点(即,$\diamond$ 类型)的模式也消费了一个 box 节点。
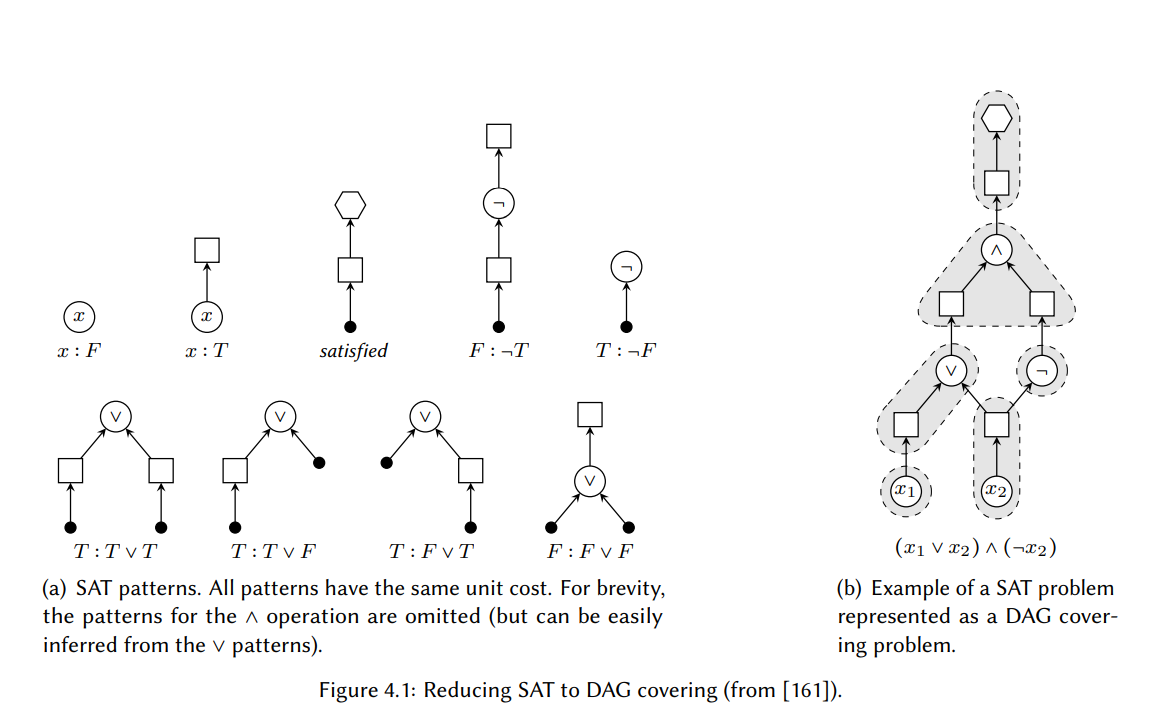
除了节点类型可以出现在表达式 DAG 中,模式也会使用额外的类型节点,我们称它为锚节点。现在,我们认为一个带有根 $p_r$ 的树模式匹配了一个节点$v\in V$,其中 V 是表达式 DAG $D = (V, E)$ 中的节点集,当且仅当:
- $type(v) = type(p_r)$,
- $|children(v)| = |children(p_r)|$,且
- $\forall c_v \in children(v), c_r \in children(p_r) : (type(c_r) = \bullet) \vee (c_r 匹配 c_v)$。
换句话说,除了可以在任意节点匹配的锚节点外,树模式的结构必须对应于已匹配的子图结构。我们也采用了两个新的定义:$matchset(v)$,它是 $P_{SAT}$ 中匹配 $v$ 的模式集合;还有$m_{p_i \rightarrow v}(v_p)$,它是 DAG 节点$v \in V$,对应于已匹配模式 $p_i$ 中的模式节点 $v_p$ 。最后,我们说一个 DAG $D = (V, E)$ 可以被映射函数$f : V \rightarrow 2^T$ 从 DAG 节点到模式覆盖,当且仅当$\forall v \in V$:
- $p \in f(v) \Rightarrow p$ 匹配 $v$ 且 $p \in P_{SAT}$,
- $in-degree(v) = 0 \Rightarrow |f(v)| > 0$,且
- $\forall p \in f(v)$,$\forall v_p \in p$ s.t. $type(v_p) = \bullet \Rightarrow |f(m_{p_i -\rightarrow v}(v_p))| > 0$。
第一个约束强制每个选定的模式都匹配了且都是实际的模式。第二个约束强制了停止节点的匹配,且第三个约束强制了剩余 DAG 的匹配。因此,$D = (V,E)$ 的一个最优覆盖是覆盖 $D$ 的映射 $f$,和最小的
$$
\sum_{v\in V} \sum_{p \in f(v)} cost(p)
$$
其中 $cost(t)$ 是模式 $p$ 的开销。
DAG 覆盖的最优方案 $\Rightarrow$ SAT 的方案
现在我们假定,如果这个最优覆盖的总开销等于 DAG 中非盒子节点的数量,则对应的 SAT 问题就成立了。因为 $P_{SAT}$ 中的所有模式恰好只覆盖一个非盒节点,且有相等的单元开销,然后如果 DAG 中每个非盒节点仅被一个模式覆盖,所以只需查看选择了哪个模式来覆盖变量节点,我们就可以简单地推断出布尔变量的真值分配。
因此,我们证明了一个 SAT 问题实例可以在多项式时间里归约成一个最优 DAG 覆盖问题实例,从而得到解决。故而,最优的 DAG 覆盖 – 也就是基于 DAG 覆盖的最优指令选择 – 是 NP-完全的。
树模式覆盖 DAG
Aho 等人的[4] 是第一篇提供在 DAGs 操作的代码生成方法的文章。在他们发表于 1976 年的文章中,Aho 等人提出了一些简单的,贪心的启发式,以及一个最优的代码生成器,其为一个可交换的单寄存器机器生成代码。但是,他们的方法假定了表达式节点到机器指令是一对一映射的,所以有效地规避了指令选择的问题。
因为最优模式选择的 DAG 指令选择在计算上是复杂的,所以第一个基于这个原理的第一个合适的方法,使用了 DAGs 来建模输入程序的表达式,但仍将模式作为树。通过这个,则开发者可以采用来自树覆盖的已知的,线性时间的方法,并将它们扩展到 DAG 覆盖。然后根据上一章我们讨论的方法,通过解决掉公共子表达式,我们可以将表达式 DAGs 转为树。我们称这个为解DAG
解表达式 DAG 为树
有两种方法可以将表达式 DAG 解DAG 为树。第一种方法是拆分共享节点的边(即,重用发生的地方),产生一组不相连接的表达式树,这些表达式树可以独立地使用通用树覆盖技术进行覆盖。通过强制将根节点在前一个共享节点的表达式树的结果写到一个特殊的位置(通常是主存),维护树之间的隐式连接。然后它们可以被其它的表达式树使用,故需要增强这些表达式树来反映这个新的输入源。使用这个方法的一个实现例子是 DAGON,它是 Keutzer[156] 开发的一个技术粘合器,将技术独立的描述映射到电路。第二个方法是在节点重用出现的地方复制一下节点, 这也可能会产生许多的树。两个概念都在图 4.2 中标明了。
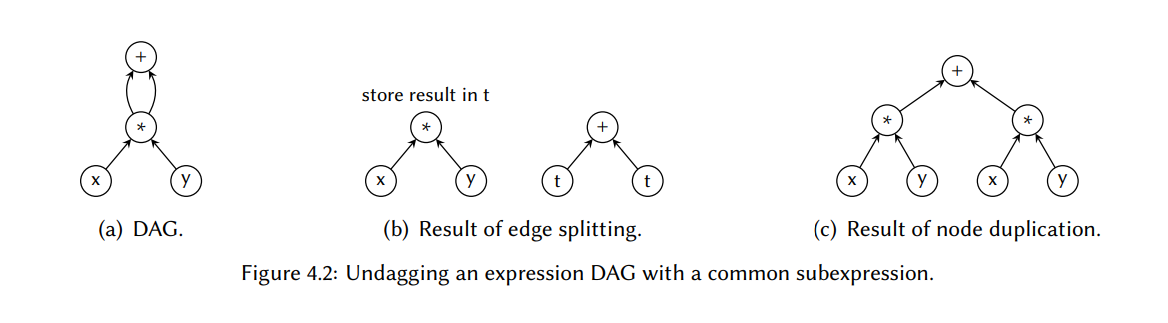
尽管解 DAG技术允许在 DAG 上使用基于树覆盖的技术来完成指令选择,但它是以牺牲性能为代价的:过于激进的边拆分阻碍了大模式的应用,因为它产生了许多小的树;同时太激进的节点复制会导致低效的汇编代码,因为有许多的操作在最后的程序中是不需要重复执行的。而且,拆分的 DAG 的中间结果必须被强制存储,这对于异构内存寄存器架构来说是比较麻烦的。Araujo 等人验证了最后一个问题 [17]。
拆分和复制的平衡
Fauth 等人[92,191] 在 1994 年提出了通过平衡节点复制和边拆分,尝试改善解 DAG 的不足。实现在了 CBC (通用总线编译器)中,它的指令选择器应用了一个倾向于复制直到开销被认为太高,这个算法才变为拆分的启发式规则。复制还是拆分的决定是通过比较两个解决方法的代价来确定的,会选择最廉价的那一个。成本是通过表达式 DAG 中的节点数量和沿着每条执行路径执行的期望节点数之间的加权和计算的(分别是代码大小和执行时间的粗略估算)。一旦完成,每个会产生的表达式树会被一个带有扩展匹配条件支持的 IBURG 的升级版覆盖(见 46 页)。但是,只是用一种方法而不使用其它的,产生的实验数据太有限了,无法判断这个技术比起将表达式 DAGs 直接转换成树的方式的效果如何。
带有协同寄存器分配目标地选择指令
在 2001 年 Sarkar 等人 [222] 开发了一个指令选择的贪心算法,有一个目的就是降低寄存器压力 – 即,汇编代码需要的空寄存器的数量 – 从而可以促进后续的指令调度和寄存器分配。因此,如果选择了一条指令,比起通常的执行周期数量,每条机器指令的成本反映的是指令导致的寄存器压力的数量(这篇文章没有详细地给出成本的计算公式)。完成指令选择首先是表达式 DAG – 表达式 DAG 已经可以通过额外的数据依赖增强成图 – 的解 DAG 成森林,通过拆分的方式,然后在每个表达式树上应用传统的树覆盖方法。有一个启发式规则可以用来决定在哪些地方执行这些削减。当选择了一个模式,由多个节点组成的模式覆盖的那些节点被归约成一个超级节点。然后,算法检查结果图是否包含任意的环;如果它包含,则这个覆盖是非法的,因为它存在循环的数据依赖。然后,修改削减并重复这个过程,直到完成有效的覆盖。
Sarkar 等人在 Jalapeño 上 – IBM 开发的一个基于寄存器的 Java 虚拟机 – 实现了他们的寄存器敏感的方法,在一小部分问题集上达成了 10% 的性能提升,因为比起默认的指令选择器,它使用了更少的溢出指令。
将动态规划扩展到 DAG
在 1999 年的论文中,Ertl [85] 给出了一个方法,不需要将 DAGs 分解成树,就可以在 DAGs 上应用传统的树覆盖方法。这个想法首先是在 DAG 上做一个自底向上地遍历,就像它是一棵树一样。然后使用我们在前一章的 3.6.2 节中讨论的传统的动态规划方法计算成本。因此,每个节点会被标记上与 DAG 通过节点复制先被归约成树时的节点相同的成本。但是,Ertl 意识到,如果几个模式都将相同的节点归约到相同的非终结符,则到这个非终结符的归约可以在规则中共享,其中的符号出现在产生式的右手边。然后可以在代码输出期间利用这个,对于每个非终结符都只生成一次汇编代码。这可以降低代码大小同时提升性能,因为降低了冗余操作的数量。图 4.3 给出了这个场景的一个示例图。在那里我们可以看到加法操作会被实现两次,因为它被两个分离的模式覆盖了两次,它们分别将子树降低到不同的非终结符上。另一方面,Reg 节点两次都被降低到相同的非终结符上(即,reg),因此可以在出现这个符号的模式规则之间共享。通过适当的数据结构,可以在线性时间里完成共享。
对于某些指令集语法,Ertl 的方法能保证得到最优的模式选择,Ertl 设计了一个名为 DBURG 的检查器,可以识别出不属于这类的语法。DBURG 的基本原理是检查每个局部最优的决策是否也是全局最优,然后在所有可能输入的 DAG 上进行一个归纳证明。为了高效地实现 DBURG,Ertl 使用了 BURG 的思路来实现(因此名命名也类似)。
进一步发展
最近,Koes 和 Goldstein[161] 扩展了Ertl 的主意,提供了一个类似与 Fauth 等人的启发式规则,即在复制的地方拆分表达式 DAG 会被认为对代码质量有负面影响的。类似于 Ertl,Koes 和 Goldstein 的算法会先执行一个类似于树自底向上遍历的过程选出最优的模式,忽略输入是 DAG 的事情。然后,在多个模式重叠的地方会计算两个成本:重叠成本,这是令模式重叠然后在最终汇编插入操作的副本的成本估算;子表达式消除成本,在相同的地方换成拆分边的成本估算。如果,子表达式消除成本低于重叠成本,则发生重叠的节点被标记为固定的。一旦这类节点全部都被处理了,会在表达式树上执行第二遍自底向上的 DP,这个时候任何模式都不允许跨过固定节点(即,一个固定节点只能在模式的根节点匹配上)。最后,一个自顶向下的过程输出汇编代码。Koes 和 Goldstein 也比较了他们自己的实现,即 NOLTIS 和线性规划的实现的比较,发现 NOLTIS 在测试用例里选择到最优模式匹配可以达到 99.7%。
直接在 DAG 上匹配树模式
不像上面的方法 – 在覆盖前将表达式 DAG 转为树 – 存在一些直接在 DAG 上匹配树模式的技术。
使用类 Weingart 模式树
在 1994 年的一篇极具影响的论文里,Liem 等人[179, 201, 205] 给出了一个设计,在 CODESYN 中实现了,CODESYN 是一个非常知名的代码分析系统,也是嵌入式开发系统 FLEXWARE 的一部分。这个方案用到了和 Weingart[256] 相同的模式匹配技术 – 我们在上一节讨论的 – 即合并所有可用的树模式到单一模式树。使用一个$O(nm)$ 模式匹配器,按顺序遍历表达式 DAG 上的模式树可以找到所有的匹配集。然后用我们之前知道的动态规划技术做模式选择(虽然没有说明它们是如何适配 DAG 的)。但是,由于使用了单一模式树,这个方法是否可以扩展成处理 DAG 模式是值得怀疑的。
LLVM
另一种 DAG 上直接树匹配的方法是应用在知名的 LLVM [167] 编译器基础设施上。根据 Bendersky[30] 的一篇博客 – 这是写作的时候除了 LLVM 代码本身唯一一篇文档 – 指令选择器基本上是一个贪心的 DAG-到-DAG 的重写器,它将机器无关的基本块 DAG 表示重写为机器相关的 DAG 表示。对于包含在表达式 DAG 中的分支和跳转的操作,进行模式匹配和其它任意节点都是相同的。模式被限制为树形式,用机器描述的格式来表示,其允许将共同特性分解到抽象指令中。使用一个成为 TABLEGEN 的工具,然后机器描述被展开成完整的树模式,其可以被匹配器生成器处理。这个匹配器生成器首先执行模式上的词法分析:先降低复杂度,它是模式大小和一个常数的和(常数可以用于调整给特定指令更高的优先级);然后增加成本;最后增加输出模式的大小。一旦排序好,每个模式都被转换成了递归的匹配器,本质是一个检查模式是否可以匹配表达式 DAG 中的一个给定节点的一个小程序。然后这个生成的匹配器被编译为字节码格式,汇编成一张匹配表,在指令选择期间进行查找。表被重新排布了从而可以按词法顺序检查模式。当找到一个匹配,会贪心地选择模式,已匹配的子图被替换为已匹配模式的输出(通常是单节点)。
虽然功能强大且使用广泛,但是 LLVM 指令选择器有几个缺点。主要的一个缺点是任意无法被 TABLEGEN 处理的模式,都必须通过客制化 C 函数手写完成。因为模式被严格限制为树形状,包含了所有的多输出模式。此外,贪心方式会对代码质量有不好的影响。
我们可以发现上述讨论过的方法共同和频繁出现的缺点是它们都是孤立地处理形状为树的模式。因此我们继续看的技术也是建模为 DAG 形式的。
线性规划选择模式
尝试以集成的方式进行代码生成–即,指令选择,指令调度和寄存器分配是同时完成的–Wilson等人【263】将这些问题描述成一个线性规划(IP)模型。线性规划【50,226】是解决组合优化问题的一种方法,而Wilson等人的1994年的论文是第一篇将IP应用到代码生成的论文。
有效的模式选择可以被表示成如下线性的不等式
$$
\forall n \in G : \sum_{p\in P_i} z_p \leq 1
$$
其中,对于表达式DAG G中的每个节点n,$n(P_i)$的匹配集中最多只有一个模式$p$会被选中($z_p$ 是一个布尔变量)。类似的线性不等式也可以表述成表达指令调度和寄存器分配的约束–这也被Wilson等人纳入到IP模型中–但这些超过了本报告的范围。此外,这个模型也可以根据目标机器的需要进行任意扩展,只需要简单地添加更多线性不等式即可,这使得它可以为异构架构进行代码生成,同时也支持相互依赖的机器指令。
比起传统的指令选择技术,解决这种整体的IP模型通常需要更多的时间,但是可以通过添加额外约束进行模型扩展的能力对于处理复杂目标机器来说是非常有价值的特性,因为它们没有任何方式可以使用传统的、启发式的方法进行建模。此外,因为IP模型使用了代码生成的所有原则,Wilson等人报告说,对于一组测试用例,它生成的汇编代码与手动优化的汇编代码质量相当,所以这意味着IP问题的最优方案可以被当成是代码生成的最优方案。因此,在本章的后面我们调研的几个技术都是基于这个先驱工作的。
将整个程序建模成DAGs
在一个将输入程序编译成微码的方法里,Marwedel【185】开发了一个称为MSSI(MIMOLA Software System)的可变目标系统。MIMOLA【272】,“Machine Independent MicroOprogramming LAnguage”的简写,它是一种处理器全数据路径建模的描述语言,不是我们平常见到的只有指令集的建模。这通常用于DSP,这种架构比较小但非常不规则。虽然MSS由几个工具组成,但是我们主要关注MSSQ编译器,因为它基本等同于指令选择。MSSQ是Leupers和Marwedel【172】开发的MSSC更快版【196】,反过来也是基于树的MSSV【186】的扩展版。
根据MIMOLA规范–它包含了处理器的寄存器和单周期里可在寄存器上执行的操作–一个被称为连接操作图的硬件DAG是可以被自动推导出来的。图4.4给出了一个例子。然后一个模式匹配器尝试在CO图里寻找子图,这些子图可以覆盖输入程序的表达式树。因为CO图包含每个寄存器的显式节点,在图中找到的一个模式匹配–被称为版本–也是一个程序变量(和临时变量)到寄存器的赋值。如果没有找到匹配,由于缺少寄存器,因此表达式树会被用赋值拆分和插入临时变量的方式重写。然后程序以递归的方式进行回溯和重复直到整个表达式树被覆盖。然后后续的过程会从每个匹配集中选出一个特定的版本,尝试调度它们从而使得它们可以被压缩到一个可以并行执行的包里。
虽然微码生成是在比汇编代码生成更低的硬件级别上进行的–汇编生成我们通常称为指令选择–但是我们也看到了必须解决的问题具有几个相似性,这是也是为什么它被包含在本报告中(更多的例子包括【27,165,182】)。在下一章中,我们会看到另一种建模了整个处理器的方法,它使用了更强大的技术。
以DAG模式覆盖DAG
许多机器指令只能被适当地建模为DAGs。例如,内置图示意的一条加载和自增指令,它从一个地址寄存器表示的内存位置加载值,同时将地址自增1。这样的指令在数组迭代中是很有用的,因为获取和增加过程可以由一条指令实现。
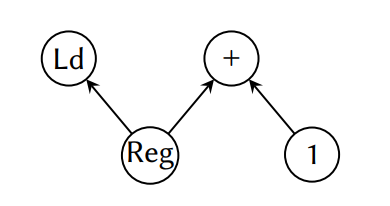
理论上,有两种方式可以完成DAG模式的模式匹配:要么通过将模式拆分成树,独立匹配它们,然后尝试将它们重新组合成原来的DAG形式;要么直接匹配它们;通常需要在平方时间里完成它们。但是我没有找到一个单一方法可以在执行直接DAG上的DAG匹配期间也被限制只有DAG。这个可能的原因是DAG匹配与子图同构的复杂度相同或者近似相同,因为后者更强大,它没有不必要和无理由的约束,如匹配器只能是DAG。实际上,在本章后面我们会看到,几个面向DAG的方法应用了通用子图同构算法来解决模式匹配的问题。
拆分DAG模式成树
前几个处理多输出机器指令的指令选择技术中的一个是由Leupers和Marwedel【168,175】开发的。在1996年的论文里,Leupers和Marwedel描述了一种方法,其中多输出指令的DAG模式–Leupers和Marwedel称为这些为复杂模式–首先根据它们的寄存器传输(RTs)被拆分成多个树模式。寄存器传输类似于Fraser的寄存器传输列表【102】,在16页的第二章中由介绍,它本质上意味着从自己树模式上可以获得的每个可观察效果。每个独立的RT反过来可能对应一到多条指令,但对于这个方式这不是严格必要的。
首先,假设之前已经执行了一个表达式DAG解析的过程,已经使用RT将每个表达式树最优覆盖成模式了。IBUG使用的语法不是手写的,而是从MIMOLA硬件描述自动生成出来的。一旦RT被选择出来,表达树会被归约成一个超节点树,其中每个表示一组被几个RT覆盖的节点,它已经被折叠成一个单节点了。因为多输出和不相交机器指令实现了多个RT,所以当机器指令被建模成RTs,则目标变成了使用已经形成的模式覆盖超级节点图。Leupers和Marwedel使用了我们之前看到的Wilson等的IP模型并进行了扩展来解决这个问题。
但是,因为选择覆盖表达式树的RTs的步骤与使用机器指令实现它们的步骤是分离的,所以生成的汇编代码不一定对整个表达式树是最优的。为了达成这个最优特性,RTs的覆盖和机器指令的选择必须是串联完成的。
扩展IP模型以支持SIMD指令
后来Leupers【170】扩展了之前提到的IP模型,从而可以处理SIMD指令。根据2000年发表的论文,Leuper的方法假设每条SIMD指令执行两个操作,两个的输入操作数是正交的。这些合在一起称为一个SIMD对,这个方法可以简单地扩展到n-输入的SIMD指令。然后,描述SIMD对的选择约束的线性不等式如下:
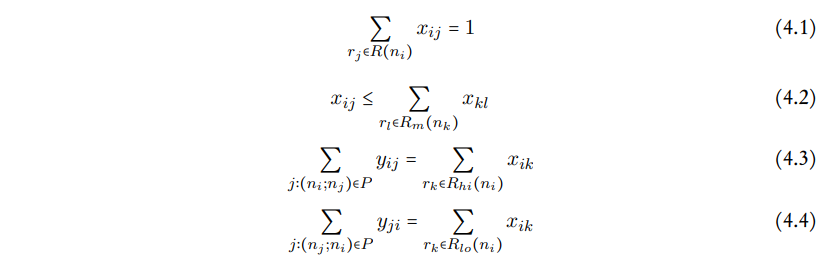
等式4.1和等式4.2保证了通用的模式选择,而等式4.3和4.4专门用于SIMD指令的。我们知道等式4.3和4.4来自Wilson等人的讨论,其强制表达式DAG中的每个节点都被一些规则覆盖;$R(n_i)$表示节点$n_i$上模式匹配的规则集,$x_{ij}$是一个布尔,表示节点$n_i$是否被规则$r_j$覆盖。等式4.2–它对于我们来说是新的–强制要求为节点$n_i$的子节点选择的规则简化为为节点$n_i$选择规则所需的相同非终结符;$n_k$是父节点$n_i$的第m个字节点,$R_m(n_k)$表示将第m个子节点归约到规则$r_j$的第m个非终结符的可用规则。等式4.3和等式4.4强制一条SIMD指令的应用实际覆盖一对SIMD对,并且任何节点最多可以被一条这样的指令覆盖;$y_{ij}$是一个布尔变量,它表示两个节点$n_i$和$n_j$是否可以被打包成一个SIMD指令,$R_{hi}(n_i)$和$R_{lo}(n_i)$表示一个分开操作寄存器高位部分和低位部分的节点$n_i$可以用的规则集。
然后目标是最大化使用SIMD指令,这通过最大化如下目标函数达成:
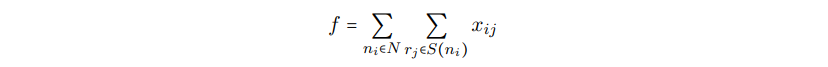
其中,N是表达式DAG的节点集,并且
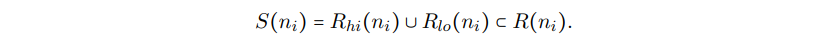
这篇论文里的实验数据表明,对于特定的测试用例和目标机器,使用SIMD指令可以降低75%的代码体积。但是,这个方法假定了SIMD指令的每个独立操作可以表示成输入DAG的一个节点。因此,不是很清楚这个方法否可以被推广到更多复杂指令的场景,也不清楚它是否适用于大的输入程序。后来Tanaka等人【238】扩展了这个工作,通过引入转移节点和转移模式,在选择SIMD指令的时候将数据转移成本也纳入了考量。
使用IP同时进行模式匹配和模式选择
在2006年,Bednarski和Kessler【29】开发了一个整合方案,使用线性规划同时解决模式匹配和模式选择。这个设计–后来被Eriksson等人使用了–是他们早期工作的一个扩展,那时候或多或少忽略了指令选择(见【152,153】)。
简单地说,IP模式假设已经为了一个给定的表达式DAG $G$生成了足够数量的模式实例。这个通过一个计算了上界的模式匹配启发式来完成的。对于每个模式实例$p$,模式包含的解决方案有:
- 将$p$中的一个模式节点映射到$G$中的一个IR节点;
- 将$p$中的一条模式边映射到$G$中的一条IR边;
- 确定$p$是否在解决方案中使用。要记住我们是有过多的模式实例的,因此它们是无法都被选中的。
因此,为了加强覆盖范围,除了我们之前见过的典型的线性不等式方程,这个IP模式也包含了保证模式实例有效匹配的等式。Bednarski和Kessler在框架里实现了这个方法称为Optimist,然后被用到了IBM CPLEX优化器【241】来解决IP模式。
当与使用集成DP方法实现相比时(也是由同一个作者开发的;见【152】),Bednarski和Kessler发现Optimist在保持代码指令的同时,实际上也能降低代码生成时间。但是,对于一些测试用例–最大的DAG表达式只包含33个节点–Optimist在设定时间限制里无法生成任何的汇编代码。一个合理的原因可能是IP模式也尝试解决模式匹配问题–这个问题我们已经看到是可以单独解决的–因此进一步使得原本就是计算复杂的问题变得更严重。
使用约束规划建模指令选择
虽然整数规划允许在模型中添加辅组的约束,但是将它们表达为线性不等式可能会很麻烦。因此,Bashford和Leupers【28】开发了一个使用约束编程(CP)的模型【217】,这是另一个解决组合优化问题的方法,它允许以更直接的形式表达约束(这在【171】中也讨论了,它是一个结合了【170】和【28】的更长版本)。简言之,一个CP模型由一组领域变量组成–每个都有一组可以假设的初始值–并且对于领域变量的一组子集,一组约束实际上指定了一个变量的有效组合。然后CP模型的一个解是所有领域变量的赋值–即每个领域变量有一个精确的值–对于所有的约束都是有效的。
类似于Wilson等人的方法,Bashford和Leuper的方法是一个整体设计,它专注于高度异构架构的DSP的代码生成。这种目标机器的指令集被分解成一组寄存器转移,然后用于覆盖表达式DAG的独立节点。由于每条RT都涉及目标机器上的特定寄存器,覆盖问题也基本上包含寄存器分配。因此,目标就是通过组合多条RT最小化覆盖成本,其中这些RT可以由一些指令并行地执行。
对于表达式DAG上的每个节点,引入一个因式化的寄存器转换(FRT),它本质上体现了一个节点匹配到所有RT。一个FRT正式的定义为
$$
(Op, D, [U_1,…,U_n], F, C, T, CS)
$$
$Op$表示节点上的操作。$D$和$U_1, …, U_n$是域变量表示这个操作的各个输入和结果的存储位置。这些通常都是可以用于这个操作的寄存器,但是也可以是虚拟存储位置,它的值是操作链中产生的中间结果(如,乘法累加指令中的乘法项J就是放在虚拟存储位置的值)。然后有一组约束保证了,如果$D$和$U_i$ 的存储位置在表达式DAG的邻近两个操作数之间存在差异,则寄存器之间存在一条有效的数据转换,或者如果其中一个是虚拟存储位置则两个是相同的。$F$,$C$和$T$是全部的域变量,均表示扩展资源信息(ERI),它表明了在特定功能单元里,会被执行的操作(F);需要的开销(C),即执行的周期数;以及使用的指令类型(T)。后来功能单元和机器指令类型被合并,和映射成特定的指令。当结果的存储位置是一个虚拟位置时,通过将C设置成0和令操作链的最后一个节点达到所需的执行周期数,多条RT可以被合并成同一条机器指令。最后一个实体$CS$是一组约束,它们定义了来自领域变量的值的范围,也定义$D$和$U_i$的依赖,还定义了对于特定目标机器需要的其它辅助约束。例如,如果一组RT匹配了由${ c = a + b, a = c + b}$组成的节点,则对应的FRT变成:
$$
{+, D, [U_1, U_2], F, C, T, {D\in{c, a}, U_1\in{a, c}, U_2 = b, D = c \Rightarrow U_1 = a}}
$$
为了简洁,我们忽略了一些细节,如ERI的约束。但是,根据这个模型,约束似乎仅限于单个FRT内,因此,阻碍了对相互依赖的机器指令的支持,这些指令的约束涉及多个FRT。
后来CP模型可以通过一个约束求解器进行优化求解–Bashford和Leupers使用ECLPS,它是基于Prolog的。但是,因为使用FRT进行优化覆盖是一个NP完全问题,Bashford和Leupers也使用的启发式来限制复杂度,即通过表达式DAG拆分成一个点上的更小的块,其中间结果可以被共享,然后在每个表达式树上独立地执行指令选择。
使用约束规划解决指令选择和IP类似,都有比较大的扩展空间,允许有额外的目标机器相关的约束添加到这个模型里。此外,这些约束应该更容易被添加到CP模型里,因为它们不需要被展开成线性不等式。但是,在写本文的时候,已经存在的解决整数规划的技术比解决约束规划的更成熟,因此潜在地使得IP求解器比CP求解器更有能力解决指令选择问题。话虽如此,但它对组合优化的技术仍然不是很清晰–它也包含了SAT–这个技术是最适合指令选择(和通常的代码生成)。
扩展语法规则包含多个产生式
受到Leupers,Marwedel和Bashford,Scharwaechter等人【224】在2007年发表的早期工作的影响,处理多输出机器指令的另一个方法是允许指令集语法中的产生式在左侧有多个非终结符。通过重复地将这些产生式作为规则和复杂规则可以将产生式中只有一个LHS非终结符的规则和包含多个LHS非终结符的规则区分开。此外,规则里的产生式的单个RHS被称为简单模式,同时复杂规则里的产生式的多个RHS被称为分离模式。我们也将分离模式的集合称为复杂模式。我们通过如下图示进一步说明:
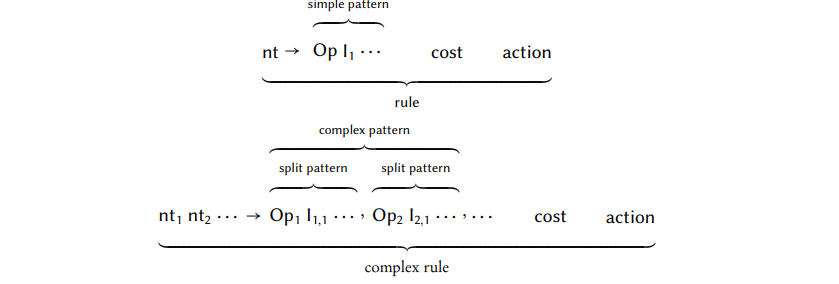
然后模式匹配的方法和我们之前看到的是一样的:匹配简单和分离模式,接着重新组合成复杂模式。模式选择器检查是否值得用一个复杂模式覆盖特定的节点集,或者节点是否应该用简单模式替代;选择复杂模式可能会对表达式DAG剩余部分可以用的模式候选产生影响,因为复杂模式内节点的中间结果不能再用于其它模式,因此可能需要复制,这会产生额外的开销。因此,如果使用简单复杂模式替换一组简单模式节省的开销大于插入的复制开销,则选择复杂模式。
在这步之后,模式选择器可能会选择重叠的复杂模式,因此会导致冲突,这需要解决。这可以通过构造一个最大权重独立集(MWIS)问题解决,在这个里面会从一个无向权重图中选出一组节点集,这些被选出来的节点是没有相交的。此外,这些被选出来的节点的权重和必须是最大的。我们会在4.5节进一步讨论这个想法。每个复杂模式都构成MWIS图上的一个节点,并且如果两个模式重叠则对应的两个节点之间会画一条边。然后这个权重计算为复杂模式里所有分离模式的成本和的负值(论文里对于如何计算分离模式的成本的介绍比较模糊)。因为MWIS是已知的NP完全问题,Scharwaechter等人采用了一个Sakai等人【221】称为GWMIN2的贪心启发式。最后,在输出代码之前,那些无法被合并成复杂模式的分离模式会被替换为简单模式。
Scharwaechter等人通过将OLIVE扩展成为一个称为CBURG的系统来实现他们的方案,并且通过为MIPS架构生成汇编代码的方式运行了一些实验。然后由CBURG生成的代码–其利用了复杂指令–会和只使用了简单指令的汇编代码进行比较。这个比较结果表明CBURG有着接近线性的复杂度,并且分别提升了25%的性能和降低了22%的代码体积。后来Ahn等人进一步开发了这个方案,包括在复杂模式里引入调度依赖冲突和将反馈循环与寄存器分配器结合起来以促进寄存器分配。
但是在Scharwaechter等人和Ahn等人的两个方案中,复杂规则只能由不连接的简单模式(即,简单模式之间没有 共享的节点)组成。在一篇2011年的论文里–它是【224】的修改和扩展版–Youn等人通过为复杂规则的特定操作数引入索引下标解决了这个问题。但是,下标被限制在模式的输入节点上,因此仍然阻碍了对完全任意DAG模式的支持。
在被标记节点上拆分模式
至今为止讨论过的方案都假定所有的DAG模式的输出是发生在跟节点上。在2001年Arnold和Corporaal【18,19,20】想出了一个方法,其可以显式地标记输出节点。然后,DAG模式将会被拆分,从而每个输出节点可以获得自己的树模式,称为局部模式;图4.5给出了一个例子。
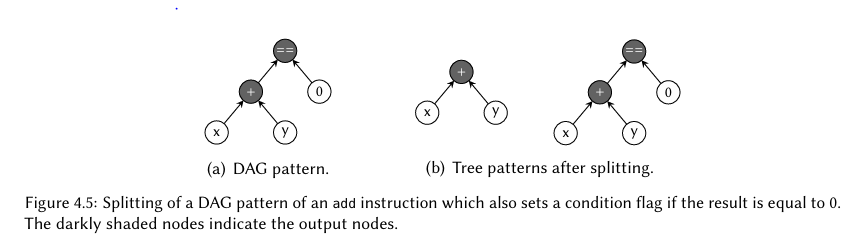
使用一个$O(nm)$的算法可以用表达式DAG匹配树模式。在匹配之后,有一个算法尝试以特定组合合并局部模式实例为全模式实例。它通过维护一个每个局部模式实例映射的覆盖输入DAG中节点的模式节点的数组,然后检查是否存在两个局部模式属于相同源DAG模式并且没有冲突来完成。换句话说,不存在对应原始DAG模式同一个模式节点的两个模式节点可以覆盖表达式DAG的不同节点。然后可以通过常规的动态编程技术完成模式选择。
Farfeleder等人【89】提出了相似的方法,通过在模式匹配上应用LBURG的扩展版,然后在第二阶段尝试重新合并那些来自多输出指令模式的匹配上的模式。但是第二阶段是由一些手写的过程组成的,它们通过机器描述自动生成。
转换语义不变的全面模式选择
Hoover和Zadeck【141】实现了一个称为TOAST的设计(Tailored Optimization and Se mantic Translation),以从一个声明式的机器描述自动化生成整个编译器框架为最终目标–包括指令选择和寄存器分配-。在模式选择期间使用语义不变转换从而更好地使用指令集。例如虽然$x*2$是语义等价于$x<<1$ –意思是x逻辑左移1位–但是当前者出现在表达式DAG时大部分的指令选择器是无法使用后者实现机器指令的,因为它们语法上和结构上都不相同。
这个方法的步骤如下:首先前端输出由语义原语组成的表达式DAG,这些原语也用于描述机器指令。然后使用派生自机器指令的单输出模式进行表达式DAG的语义匹配。语义匹配被称为toe prints,由语义匹配器找到,当语义匹配失败的时候,这个匹配器采用了语法匹配语义转换不变相结合的方式–即相同类型的节点,它被实现为一个直接的模式匹配器$O(nm)$。转换只有当它后面会产生一个语义匹配的时候才会采用,它会对所有的可能的脚踝印产生一个有边界的全搜索。一旦所有的脚踝印都被找到了,它们会被合并到足迹里,它对应于机器指令的全部效果。因此,只会有一个(与单输出指令相同)或者几个(与多输出指令相同)脚踝印。但是,这篇论文缺少如何准确实现的细节。最后,所有足迹的组合都是为了获得一个使得表达式DAG最有效实现的情况。但是为了减小搜索空间,这个过程只考虑了一种组合,即每个被选择的足迹至少语法匹配上表达式DAG里的一个语法原语,并且表达式DAG只有很少的节点,如常量可能会被包含到多个足迹里。
但是,由于这个方法的穷举性,在它当前的形式下,它不太能为除了最小输入程序外的其它程序生成汇编代码;在作者实现的原型里,对于测试例子中的一个,它报告了将近$10^{70}$“隐式指令匹配”,并且不清楚它实际使用了多少个。
归约模式选择为一个MIS问题
有许多的方法可以将模式选择问题归约为一个最大独立集问题(MIS);我们已经在Scharwaechter等人和Ahn等人的应用(见4.4.1节)里看到过这个方法,在这一个节和下一章中我们还会遇到更多这种方案。因此,我们会进一步详细地描述这个技术。
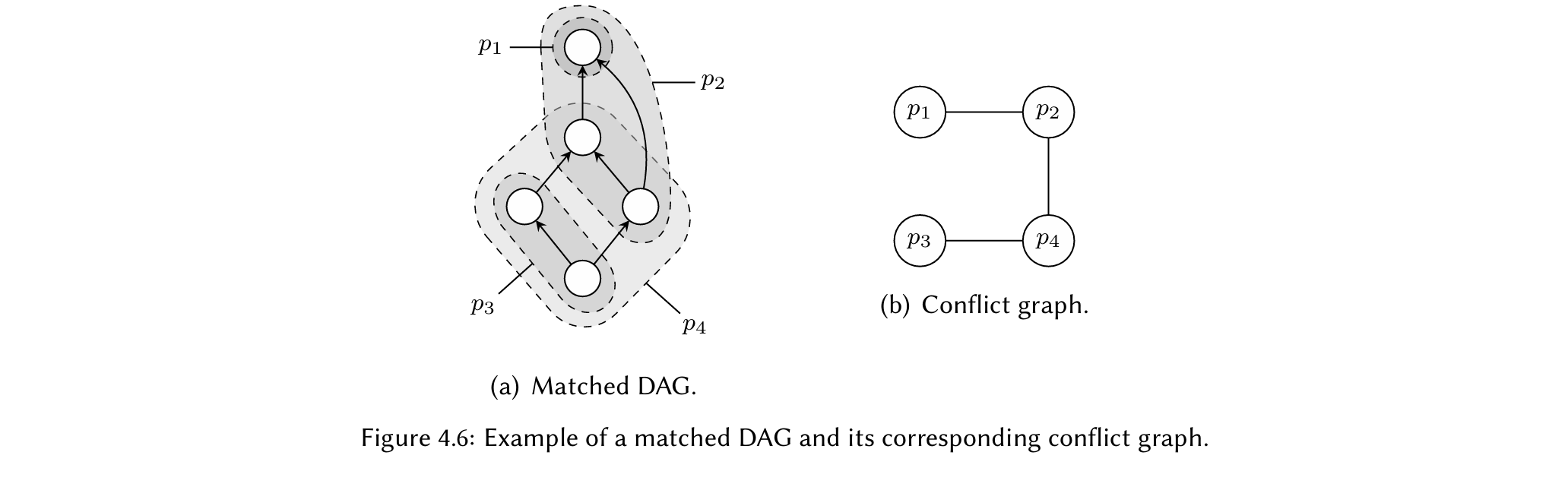
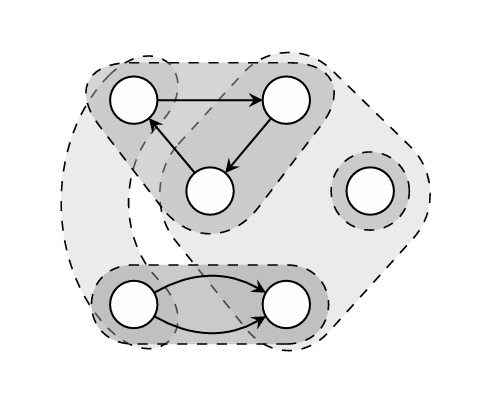
对于覆盖表达式DAG一个或者多个节点的模式,会构造一个对应的冲突或者干涉图。图4.6给出了一个例子。在匹配了的DAG里,如图(a)所示,我们看到$p_1$和$p_2$重叠了,$p_4$和$p_2$、$p_3$重叠了。对于每个模式,我们在冲突图$C$中构建一个节点,如图(b)所示,然后在任意两个重叠的模式的节点之间画一条边。通过选择一个C节点的最大集使得C中的所有被选择的节点不相交,我们会获得一个模式集合使得表达式DAG中的每个节点都被完全覆盖了并且模式之间都没有重叠。这个问题如预期一样是个NP完全的问题。
为了获得最优的模式选择,我们可以将模式成本作为冲突图里每个节点的权重,因此将这个MIS问题扩展为最大权重独立集问题(MWIS),选择一个最大顶点集$S$使得它满足MIS以及最大的$\sum_{s\in S}weight(s)$。因为MWIS有一个最大的目标,我们简单地将每个权重赋为模式的负成本。需要注意的是这个技术不仅限于DAG模式的选择,也可以用于图模式。
使用MIS和MWIS的方法
在2001年,Kastner等人【151】开发了一个面向混合可配置系统指令集生成的方案。因此,模式不是作为输入而是作为问题本身生成的一部分(这个也在下一章中讨论到了)。一旦模式已经生成,则使用一个来自【75】的通用子图同构算法来寻找表达式DAG里的所有模式匹配。子图同构会在下一章中详细描述。然后实例化相应的MIS问题,它通过启发式方法求解。因为,这个匹配算法不需要输入是DAG,这个方式可以扩展成任意基于图形式的输入。在这个论文的扩展版,Kastner等人【150】提高了模式匹配算法从而快速剔除不相同的子图。但是不保证产生一个最有的模式选择。
处理回环指令
Brisk等人【37】也将MIS的思想用于提升带有回环指令的目标机器的指令选择上。回环指令是汇编代码中的小标记,表示返回到前一区域重新执行。因此,汇编代码本质上是使用LZ77算法【274】里应用的方法进行压缩,其中字符串可以被压缩替换为字符串里早期出现的通用子串的指针,并且可以通过简单的复制粘贴重构。因为回环指令不会导致跳转或者过程调用,所以其结果会降低代码体积并且对于性能是零开销的。
因此,模式集对于指令选择是不固定的,但必须在模式匹配之前确定好。模式是通过将表达式DAG中相邻节点聚集在一起形成的。如果一个模式可以使得代码体积降低最多则会被选定,然后通过重复使用新的节点替换模式实例更新表达式DAG来表明回环指令的使用。这个过程会一直重复直到无法找到新的模式好于一些用户定义的标准值。类似于Kastner等人的,Brisk等人的设计也使用子图同构来寻找这些模式,只是使用的是不同的算法称为VF2【60】。虽然这个算法在最坏情况下展示了$O(nm)$的复杂度,但是作者报告在实验中它在大部分表达式DAG运行的更高效。
其它基于DAG的技术
扩展均值-终点分析到DAG
在【194】之后20年,Cattell等人发布了他们自顶向下树覆盖方法(见前一章的3.4.1节),Yu和Hu【270,271】重新探索了均值-终点分析作为一种指令选择方法,并进行了两个主要的提升。首先,这个新设计处理了表达式DAG和DAG模式,这些【194】和Cattell等人的方法被限制在了树。第二,它将均值-终点分析和分层规划【220】结合在一起,分层规划是一种搜索策略,它可以识别出许多问题可以分层方式处理,能够解决更大更复杂的问题。这也使得搜索空间可以被详尽地探索,并且避免死终点场景和无限地循环,这些是直接实现的均值-终点分析可能会遇到的问题(【194】,并且在到达某一特定搜索空间深度的时候,Cattell等也通过强制剪枝规避这个问题)。
虽然这个技术展示了最坏时间执行场景,它是搜素深度的指数,但是Yu和Hu在他们的论文里宣称深度3就足够生成和手写汇编一样质量的代码。但是,不清楚这种方法是否可以处理复杂的指令,如具有不相交输出或内循环属性的指令。
类似DAG的网格图
在1998年,Hanono和Devadas【130,131】提出了一个类似于Wess的使用网格图思路的技术–我们在3.7.5节讨论过的–他们在一个称为AVIV系统里实现了。这个指令选择器使用一个表达式DAG作为输入,根据操作可以运行的目标机器上的功能单元的数量复制每个节点。在每个重复节点前后可以插入特殊的拆分和转换节点,从而使得数据流可以分岔,然后在传递到表达式DAG里的下一个节点之前重新收敛。使用转换节点也允许从一个功能单元到另一个功能单元的数据传输成本被纳入考量。类似于网格图,指令选择则被归约为寻找一条从根节点到表达式DAG左叶子节点的路径。不像Wess的面向最优动态规划的方法,Hanono和Devadas使用了贪心启发式,其从根节点开始向着叶子节点方向去。
但是,类似于Wess的设计,这个技术假设了表达式节点和有效机器指令之间一对一的映射;事实上,AVIV的主要目标是为VLIW架构(超长指令字)生成高效的汇编代码,它的重点在于将尽可能多的操作组合到同一个指令包中。
总结
在这章中,我们研究了几个基于DAG覆盖原理的方法,DAG覆盖是树覆盖的通用性。在DAG而不是树上操作有几个优势:更重要,通用的子表达式和最大机器指令集–包含多输出指令和交叉输出指令–在指令选择期间可以直接建模和利用这些指令,从而可以提高性能和降低代码体积。因此,基于DAG覆盖的技术是今天现代编译器中最常被使用的技术之一。
但是,从树变成DAG的无限成本使得最优模式选择无法在线性时间里达成,因为这个问题是NP完全的。在相同的时间里,DAG的表达能力不足以正确建模输入程序和机器指令模式的所有方面。例如,for循环语句会导致表达式图带有回边,因此限制了DAG的范围在基本块里。这显然也会排除内循环指令的建模。另一个缺点在于存储程序变量和临时变量以不同的形式和跨函数不同的位置的优化机会。我们会在下一章中看到一个例子,它可以通过这个提升最终汇编代码的性能。
在下一章中,我们将会讨论最新且最通用的指令选择原理–图覆盖–它解决了上述DAG覆盖的一些缺陷。
基于图的方法
即使是我们上一章研究的 DAG 覆盖,比起树覆盖有更通用和更强大的形式,它仍然不足以处输入程序和机器指令的所有方面。例如,for 循环语句导致的控制流无法建模成表达式的一部分,因为它需要循环,这违背了 DAGs 的定义。通过移除这个限制,我们最终得到最通用的形式,即图覆盖。
原理
就像 DAG 覆盖是树覆盖更通用的形式一样,图覆盖也是 DAG 覆盖更通用的形式。通过允许输入程序的两个语句采用任何通用的形状,指令选择可以从之前的局部范围扩展开 – 即,从覆盖一个表达式树或 DAG – 到一个全局范围,它包含了整个函数中的所有表达式,因为图形能够建模控制流。这被称为全局指令选择,理论上它使得指令选择器可以跨基本块边界移动操作,从而可以更好地利用具有大模式的复杂机器指令,否则这些指令是无法用上的。对于现代机器,功耗和热辐射是变得越来越重要的因素,解决这些问题的一个关键方法是使用更少的,且更大的指令,它们比起使用更多更小的指令的功耗会更小。
但是,从 DAG 模式到图模式的转变,由于模式匹配变成了 NP-完全的问题,我们不能够再采用树和 DAG 的模式匹配技术;图 5.1 给出了在使用不同图形时的模式匹配和最优模式选择的不同时间复杂度。此外,我们需要应用到通用子图同构算法,因此从研究一些这样的算法开始。

使用子图同构的模式匹配
子图同构的问题是去识别一个任意的图$G_a$ 是否可以通过反转,扭曲或者镜像变成另一个图 $G_b$ 的子图。在这个场景中,我们说$G_a$ 是 $G_b$ 的同构子图,并且确定它是个已知的 NP-完全问题[58]。因为同构子图在许多其它的领域都可以找到,所以对这个问题进行了大量的研究(见例子[60, 87,88,109,129,139,163,234,248])。在这节中,我们会专注于 Ullman 算法和另一个常用算法 VF2。
需要注意到的是这些模式选择技术只检查同一结构而不是同一语义。例如,表达式$a*(b+c)$和$ab + ac$是功能相同的,但是产生了不同的结构图,因此无法相互匹配到一起。Arora等人【21】提出了一个方法在模式选择之前先标准化图,但是它被限制在算术表达式DAG上,并且不保证找到所有的匹配。
Ullman算法
其中第一个–并且是最出名的–判断子图同构的方法是UllMann【248】开发的一个算法。在他的论文里,发表在1976年,Ullmann将确定图$G_a = (V_a , E_a)$是否是另一个图$G_b = (V_b , E_a)$的同构子图的问题简化为寻找一个满足如下条件的布尔矩阵$|V_a|$x$V_b$ M:
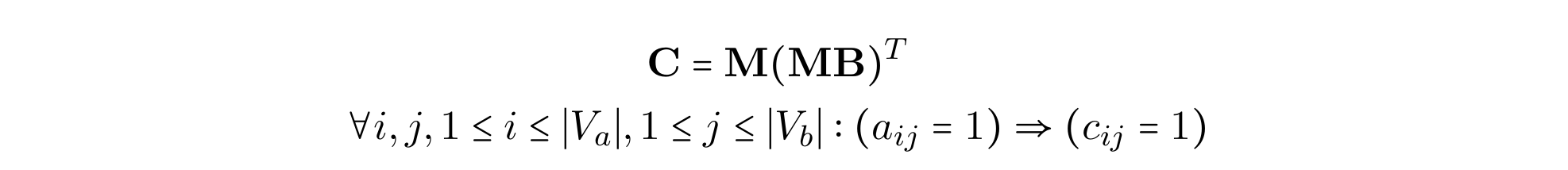
A和B是$G_a$和$G_b$各自的邻接矩阵,$a_{ij}$和$c_{ij}$是A和C的元素。当这些条件满足,M里面的每列只有1个,M里的每一行最多只有1一个。
可以通过暴力求解的方式寻找M,先初始化每个元素$m_{ij}$为1,然后每次迭代修剪掉1直到找到解法。为降低搜索空间,Ullmannn开发了一个例程,消除了一些一定不会出现在所有解法里的1。但是根据【60】,即使有这个提升,这个算法的复杂度仍然有$O(n!n^2)$。
VF2 算法
在2001年Cordella等人在论文里【60】提出了VF2算法,它已经被用在了几个基于DAG或图覆盖的指令选择器里。特别是,它被用在了辅助指令集提取(ISE),有时候也被称为指令集选择。在【10,53,192】里给出了这些方法的使用例子,Galuzzi和Bertels【110】有一个现状的调查文章。
概括地说,VF2 算法递归地构造一个$(n,m)$对的映射集,其中$n \in G_a$,$m\in G_b$。这个算法的核心是用于检查一个新的候选对是否允许被包含到映射集里的规则集。这个规则意味着一组语法可行性检查,由$F_{syn}$实现,接着是语义可行性检查,由$F_{sem}$实现。无需赘述任何细节,我们将$F_{syn}$定义为
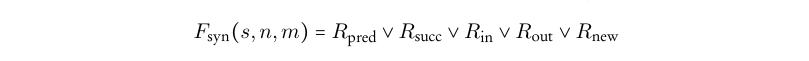
其中$n\in G_a$,$m\in G_b$–因此构成候选对–$s$表示当前的(局部)映射集。前两个规则–$R_{pred}$和$R_{succ}$保证了新的映射集$s^`$和$G_a$、$G_b$的结构是一致的。剩下的三个规则用于精简搜索空间:$R_{in}$和$R_{out}$通过保证$G_b$里仍然存在足够的非映射节点可以映射到$G_a$里剩余的节点,从而在搜索空间里向前看一步,类似的$R_{new}$向前看两步。这些规则的精确定义在相关的论文里都有解释, 它们经过小量的修改可以保证图同构而不是子图同构;对于前者,$G_a$和$G_b$的结构必须是严格相同的,在它们匹配之前不能扭曲或者反转。然后$F_{sem}$是一个框架,可以方便地添加候选对里的节点的额外检查。
在最坏情况下,这个算法表现出了$O(n!n)$的复杂度,但是最好的时间复杂度–多项式的–让它可以实际应用于非常大的图的模式选择;有报告说VF2算法已经成功地用在了包含上千个节点的图上【60】。
基于图的模式选择技术
DAG覆盖和图覆盖最主要的区别是,后者的模式选择问题更加的复杂,因为它NP完全的。但是解决模式选择的技术通常都足以应用在两个两个原理上。在这节中,我们会寻找更多的模式选择技术,它们通常通过基于图覆盖的方法首次出现在指令选择中。
一元和二元覆盖
我们将讨论的第一个技术是一个方法,它处理的模式选择问题是可以被转换成等价的一元或者二元覆盖问题。除了一个细节之外,两者背后的概念是相同的。虽然首先出现的是基于二元覆盖的技术,但是我们会从解释二元覆盖开始,因为二元覆盖是一元覆盖的扩展版。
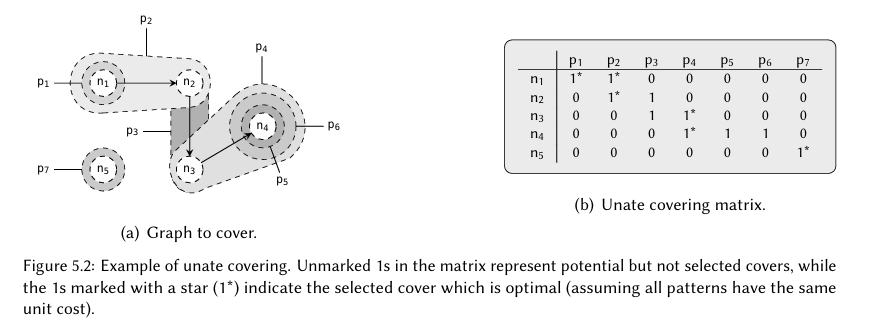
一元覆盖
一元覆盖的思路是创建一个一元矩阵M,其每一行表示表达式图上的一个节点,每一列表示一个匹配了一个或者多个表达式节点的模式的实例。如果我们将M的第$r$行第$i$列表示为$m_{ij}$,则$m_{ij}=1$表明节点$i$被模式$j$覆盖了。然后这个模式选择的问题可以被归约为寻找一个M的有效配置使得每一行的和至少为1。这个问题如图5.2所示,显然是一个NP完全的问题,但是存在几个有效的技术可以启发式地解决它(如,【61,123】)。
但是仅有一元覆盖无法包含模式选择的所有依赖,因为一些模式需要–和忽略–其它模式的选择才能生成正确的汇编代码。例如,假设图5.2里的模式$p_3 $需要模式$p_6 $被选出来覆盖$n_4$,而不需要模式$p_5$。在指令集语法中,这是通过非终结符强制执行的,但是对于一元覆盖来说,我们没法表达这个约束。因此我们进而使用二元覆盖,它是有可能解决这个问题的。
二元覆盖
我们首先将来自一元覆盖问题的布尔矩阵重写为布尔公式,其由交集并集组成。我们称每个并集–其由字符和$\vee$操作组合组成–为闭包。然后闭包反过来由$\land$组合。因此图5.2(b)里的布尔矩阵可以被重写为
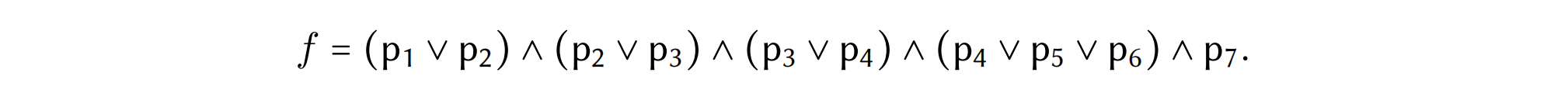
不想一元覆盖,二元覆盖允许闭包里出现补集字段,我们写为$\overline{x}$。前面提到的如果$p_4$被选择了则$p_6$也会被强制选择的约束现在可以表示成
$$
\overline{p_4} \vee p_6
$$
然后它可以被添加到布尔公式$f$。这个称为隐式闭包,因为它逻辑等价于$p_4 \Rightarrow p_6$。
基于一元和二元覆盖的方法
根据【56,177,178】,Rudell【218】在他的1989年的博士论文里开创性地使用了二元覆盖,将其应用在解决DAG覆盖,作为VLSI综合的一部分。Liao等人【177,178】随后在1995年为单寄存器目标机器优化代码体积的方法里将其应用到了指令选择里。为了限制搜索空间,Liao等人的方法在两次迭代里解决了模式选择问题:在第一次迭代里忽略了必要的数据转换的成本。在选出模式后,被相同模式覆盖的节点被折叠刀单个节点里,然后构造了第二个二元覆盖问题来最小化数据转换成本。虽然可以同时解决这两个问题,但是Liao等人没有这样做,因为这样做必要的闭包数量会变得极端的多。Cong等人【56】最近应用二元覆盖作为解决可配置处理器架构的应用相关指令生成。
一元覆盖已经被Clark等人【54】成功地应用到了无环计算加速器的汇编代码生成里,其可以局部客制化从而提高当前执行程序的性能。根据推测,如果目标机器足够同构,则就不需要隐式闭包里。后来Hormati等人扩展了这个方法【142】,用于降低加速器设计的互连和以数据为中心的延迟。在2009年Martin等人【183】也将一元覆盖的思想应用到了解决有关于可配置处理器扩展的相似问题上,但是要将其建模为约束编程问题,这也合并了指令调度的约束。此外,他们在独立的例程里使用CP来寻找所有的可用模式匹配。
基于 CP 的技术
虽然Martin等人前面的方法使用了约束编程,但是模式选择的约束是一元覆盖的一个简单的直接编码,因此并不特定于 CP 本身。当后来Floch等人【97】使用CP模型来处理带有可配置单元结构的处理器的时候,他们用完全不同与一元覆盖的约束替换了模式选择的方法。此外,不像我们在前面章节最早看到的Bashford和Leupers【28】的开创式的CP方法,这个设计使用了模式匹配和模式选择的更传统的形式,而不是将模式分解为RT,然后选择可能合并更多的RT的机器指令。
在Floch等人的CP模型里,满足每个表达式节点必须被有且仅有一个模式覆盖的要求是强制满足COUNT($i, var, val$)约束,其表明在一组领域变量$var$里,准确的$val$变量数量必须假设为值$i$,$val$必须是固定数量或者表示另一个领域变量。让我们假设表达式图里的每个节点都有一个相关联的匹配集,其包含了所有可能覆盖这个节点的所有模式,然后每个出现在匹配集里的模式$m$都已经被赋值了一个唯一的整型值$i_m$。我们为每个表达式节点$n$引入了一个领域变量$match_n$来表示被选出来覆盖$n$的模式。对于每个模式$m$,我们也引入了一个领域变量$nodecount_m \in {0, size(m)}$,其中$size(m)$是$m$中模式节点的数量,然后定义$mset_m = \cup_{n\in nodes(m)} match_n$作为模式$m$里可能出现的$match_{n}$变量集。使用这个,我们可以将每个表达式节点必须被准确覆盖表达为
$$
\forall m \in M:COUNT(i_m, mset_m, nodeount_m)
$$
其中,M是匹配模式的总集。这个约束比一元覆盖的更有约束性,产生了更多的传播,其降低了搜素空间。为了识别哪个模式被选择了,我们简单地检查了每个模式m的$nodecount _m > 0$是否成立。
这个模型被Arslan和Kuchcinski【22】进一步扩展来容纳VLIW架构和不相交输出的指令。这个本质上是通过拆分每个不相交输出指令为多条子指令完成的,每个都由一个不相交模式建模。使用一个通用子图同构算法来寻找所有的模式匹配,然后模式选择被建模成CP模型的一个实例,它有一个子指令被调度的额外约束,从而他们可以被原始不相交输出机器指令替换掉。因此这个技术不同与我们之前已经看到的方法(如,Scharwaechter等人的【224】,Ahn等人的【2】,Arnold和Corporaal【18,19,20】的),它的局部模式被重新合并成复杂模式实例的优先级高于模式选择。这个设计假设了表达式图里没有循环,但是它可以由多个不连接的图组成。
然而,在所有的CP模式里包括Martin等人的,Floch等人的,Arslan等人的和Kuchcinski的,它们的目标机器都被假设为有一个同构的寄存器架构,因为它们没有建模不同寄存器类型之间的必要数据转换。
基于 PBQP 的技术
在2003年,Eckstein等人【77】提出了一个方案,在模式选择期间使用了一个称为PBQP的建模方法,其使用了SSA图作为输入,它是少数几个解决全局指令选择的技术之一。因此我们会更详细地讨论这个方案,但是我们首先解释几个对于我们来说是新的概念。我们从描述SSA开始。
重写输入程序为SSA形式
SSA表示的是静态单一赋值,是一种程序表示的形式,其在大部分编译器书(我推荐【59】的)里都有好的解释了。本质上,SSA限制了函数里的每个变量或者临时量都只被定义一次。这个的效果是每个变量的生命周期(即,在这个代码长度里,变量的值不会被破坏)都是连续的,这反过来意味着每个变量都对应单一值。这个的结果是可以简化许多优化例程,几个现代编译器都是基于这个形式的(如,LLVM和GCC)。

但是,这个只定义一次的限制在变量有多个来源的时候会导致问题,这种情况在IF语句和for循环的时候会发生。例如,如下C函数(它在计算阶乘)不是SSA形式,因为f和i被定义了多次(分别是在2和3行,以及6和7行)。这种情况下通过使用$\phi 函数$来解决,这允许变量值使用多个值中的一个进行定义,它们每个都来自特定的基本块。通过声明额外的变量和在循环块开始的地方插入$\phi$函数,我们可以将上述例子重写为SSA形式:

$\phi$函数的问题是现在我们需要确定使用哪个值。例如,在上述SSA代码的第6行里–第7行也是类似的–我们在第一次循环迭代的时候使用$i_1$的值定义$i_2$,然后在接下来的循环迭代里使用$i_3$的值。但是,关于这些如何处理的细节超出了我们目的的范围,因为我们后面最感兴趣的是SSA图,这类似于表达式图。我们很快会见到一个例子。
全局指令选择有收益的一个例子
Eckstein等人意识到将指令选择限制在局部范围会减少为专用数字信号处理器生成定点算术汇编代码的代码质量。DSP的一个通用特性是它们的定点乘法单元经常让结果左移一位。因此,如果是从定点乘法累积计算得到的值,需要将它保存到移位模单元直到所有的定点乘法都执行完,否则累计值将会有不必要地来回移动。
在图5.3(a)里,我们看到了一个可能发生这种情况的 C 函数示例。一个定点值s被计算出来作为两个定点数组a和b标量产物。为了高效地在DSP上执行,s的值需要被存储在for循环里的(行3-5)移位模式里,并且只在返回之前移回(行6)。在一个指令集语法里,它可以通过引入一个额外的表示移位模式的非终结符进行建模,然后通过生成合适的移位指令,添加一条将移位模式转换为正常模式的规则。
但是,如果指令选择器每次只是考虑一个基本块,则这个模式的有效使用是难以达成的,因为s的定义和使用出现在不同的表达式树上(见图5.3(b))。与之相对应的是,SSA图的所有定义和使用都是出现在同一张图上。在图5.4里我们可以看到相同函数的SSA形式和它对应的SSA图。需要注意的是SSA图没有包含任何表示控制流的节点,其是分开处理的。此外,为了将生成的汇编代码放入到基本块里,指令选择器需要将原始的IR代码作为额外的输入。
使用PBQP解决模式选择
在Eckstein等人的方法里,解决模式选择问题的方法是将其归约到划分布尔二次问题(PBQP)。PBQP是由Scholz和Eckstein【225】在2000年首次引入的,用于解决寄存器分配问题,它是二次赋值问题(QAP)这个基本的组合优化问题的扩展版。QAP和PBQP都是NP完全的,因此Eckstein等人开发了他们自己的启发式求解器,其发表在2003年的相关论文里。我们通过从定义开始自底向上构造模型来解释PBQP。
首先,这个设计假设了机器指令是通过线性形式的语法给出的–这个在第3章第51页介绍过了–其中每条规则要么是基本规则要么是链式规则。对于SSA图中的每个节点n,我们定义一个布尔向量$r_n$,其长度等于匹配节点的基础规则的数量。因为每个产生式都是线性形式的,一个模式匹配只需要基础规则的树模式的操作符匹配SSA图里的节点的操作符号。
选择每个基本匹配规则的成本是由另一个向量$c_n$的同一长度给出的,其每个元素是根据节点操作的估计相对执行频率加权的规则成本。对于循环里的操作,需要给一个更高的优先级到低成本指令上,因为它们对性能会有更大的影响。根据这个,我们可以定义一个覆盖SSA图的成本函数f为
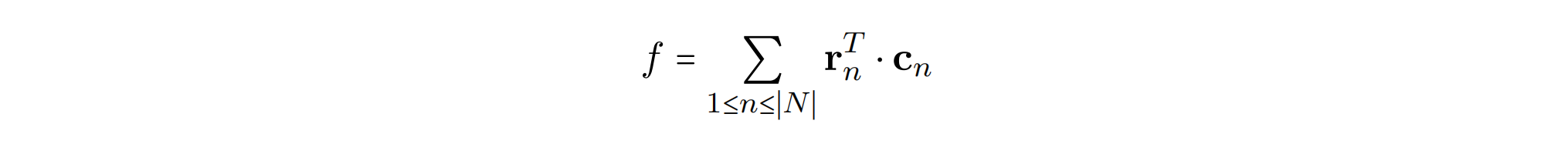
其中$|N|$是节点的数量。我们称这个为累计的基础成本,因为它给出了正用于覆盖这个SSA图的基本规则的总成本,目标是当覆盖完SSA节点且每个节点只覆盖一次的时候(即$\forall 1 \le n \le |N|:r^T_n \cdot c_n$)f的值最小。
但是,这不一定会产生高效地覆盖,因为基本规则之间是没有联系的,意味着一个被选择的基本规则可能被归约到的非终结符与另一个被选择的规则所需的非终结符。通过为SSA图中的每对存在一条从m到n的直连边的节点n和m引入一个成本矩阵$C_{nm}$可以解决这个问题。然后$C_{nm}$中的元素$C_{ij}$表示了为节点n选择的规则i和为节点m选择的规则j的成本,并且这个值会被设置为如下:
- 如果规则j归约m到一个终结符,这个终结符是规则i的产生式的右侧的某个位置期望的,则$C_{ij} = 0$。
- 如果规则j产生的非终结符可以通过一串链式规则被归约到一个期望的非终结符,则$c_{ij} = \sum c_k$,其中$c_k$一个被应用的链式规则k的成本。
- 否则,$C_{ij} = \infty$,这会阻止选择此规则组合。
这些链成本是通过计算所有链规则的传递闭包来计算的。对于这个,Eckstein等人似乎使用了Floyd-Warshall算法【98】,后来Schäfer和Scholz【223】 发现了一个通过寻找规则链的最优序列计算每个$c_{ij}$的最低成本的方法。最新的方式是,这个成本是根据执行频率获得的权重。
现在我们通过添加累积的链式成本参数化f,从而获得
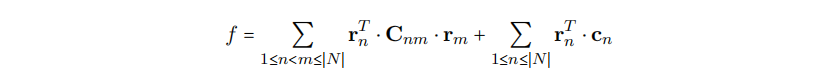
它可以通过使用一个启发式PBQP求解器求解(也是Eckstein等人开发的)。
精明的读者在这个时候可能已经注意到这个方案假设了SSA图不是一个多图–即,同一对节点之间可以存在多个边的图–这妨碍了诸如$y = x + x$的表达式的直接建模。幸运地是,这样子的边可以通过引入临时新的变量然后通过值拷贝链接它们来移除掉(见内联代码)。
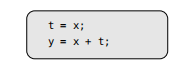
Eckstein等人在一个被选择的DSP问题集上测试他们的实现,这个问题集这凸显了全局指令选择的必要性;结果表明这个方法比起传统的基于树的指令选择器,平均能提升40-60%的性能–有一个问题有82%的提升。性能里的高收益来自于基于树的方法的限制,这个限制导致程序变量必须预先分配一个非终结符,这个对于代码质量可能会有负作用的影响;如果选择不当,则必须插入额外的汇编代码来撤销这些决定,因此会降低性能。不幸地是,Eckstein等人的设计被限制在树模式里,这阻碍了许多通用目标机器特性的开发,如多输出指令。
扩展PBQP到DAG模式
在2008年,Ebner等人【76】将Eckstein等人的PBQP模型扩展到DAG模式的处理上。通过替换LLVM2.1上默认的指令选择器–一个贪心DAG重写器–对于一组被选定的编译到ARMv5处理器的问题,生成的汇编代码的性能平均提高了13%,并且编译时间基本没有影响。
首先扩展了语法规则从而允许一条规则包好多个产生式–我们称这些为复杂规则–这扩展的方式和Scharwaechter等人的方式是类似的【224】(参见上一章第 72 页)。我们认为复杂规则里的每个产生式构成一条代理规则。然后增强PBQP问题使其可以处理复杂规则的选择,这个实际上是引入新的向量和矩阵用于确定是否选择复杂规则以及强制选择所有相应代理规则的约束。我们也需要防止那些会增加数据循环依赖的复杂规则组合。
当成本矩阵超过一个的时候,就变成需要去识别区分它们。我们称所有的基本和代理规则属于$B$分类,所有的复杂规则属于$C$分类。然后一个成本矩阵可以写成$C^{x\rightarrow y}$,这表示它是从 X 类过渡到 Y 类的成本。作为一个例子,我们之前用于计算累积链式成本的成本矩阵之后可以写成$C^{B\rightarrow B}_{nm}$,因为它只关心基本规则。现在我们可以进行PBQP模型的增强了。
首先,对于SSA图中的任意节点n,$r_n$向量使用n匹配的代理规则进行扩展。如果两个或者更多从不同复杂规则派生出来的代理规则是相同的,则向量的长度只增加1。第二,对于不同节点的每个排列,我们都会创建一个复杂规则的实例,其中匹配到的代理规则可以被组合成一个复杂规则。每个实例都会产生一个2-元决策向量$d_i$, 它表示一个复杂规则实例$i$是否被选择了(即,在第一个元素里的1表示没有被选择,在第二个元素表明被选择了)。然后我们累积被选择的复杂模式的成本,就像我们为基本规则做的一样,将其添加到f,其中I是复杂规则实例的数量,$C^C_i$是2元成本向量,它的元素要么是0要么是复杂规则的成本(取决于$d_i$的排列)。
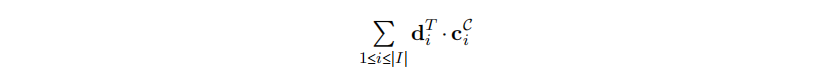
如前所述,为了选择一条复杂规则实例$i$,$i$的所有代理规则必须都被选择出来。我们通过一个成本矩阵强制完成这个,其中n是SSA图中一个特定节点,i是复杂规则的一个特定实例。然后$C^{B \rightarrow C}{ni}$里的一个元素$c{mj}$按如下规则设置:
- 如果j表示i没有被选择,则$c_{mj} = 0$。
- 如果m是没有被关联到复杂规则i的基本或者代理规则,则$c_{mj} = 0$。
- 否则,$C_{ij} = \infty$。
因此添加
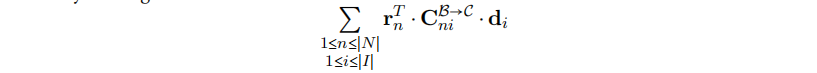
到f, 如果$d_i$设置成被选择的,则我们强制选择必要的代理规则。
但是如果所有代理规则的成本是0,则这个解是可行的,即复杂规则的所有代理规则都被选择了,但是实例本身没有被选择。Ebner等人通过给所有的代理规则设置一个高成本M,并修改了所有的复杂规则的成本为$cost(i) - |iM|$解决了这个问题,其中$|i|$是复杂规则i所需的代理规则的数量。 这抵消了所选代理模式的人为成本,因此降低所选代理规则和复杂模式的总成本*cost(i)*。
最后,我们需要一个成本矩阵$C^{C\rightarrow C}{ij}$,其可以防止两个复杂模式实例i和j被同时选择出来,如果它们是重叠的或者组合在一起会引入循环数据依赖。这是通过设置$C^{C\rightarrow C}{ij}$里的对应这个场景的元素为$\infty$,或者为0,并相应地增加f。因此f完整的定义变成:
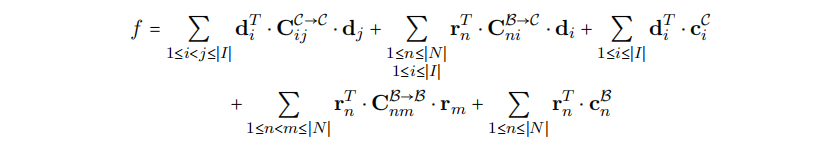
使用重写规则替代语法规则
另一个基于PBQP的技术是Buchwald和Zwinkau【39】在2010年提出的。不像Eckstein等人和Ebner等人的,Buchwald和Zwinkau将指令选择视为形式化的图转换问题–之前的很多工作已经存在–并将机器指令表达为重写规则而不是语法规则。通过使用形式化的基本规则,指令选择器可以被验证,它可以使用一个自动化工具处理所有可能的输入程序;如果检查是失败的,这个工具可以提供指令集缺失的必要的重写规则。
Buchwald和Zwinkau的方法如下:首先通过把$\phi$节点拆分成两个节点,将SSA图转换成一个DAG,这可以高效地打破循环。当找到SSA DAG的所有可用的重写规则–通过使用传统的模式匹配完成的–会构造出一个相应的PBQP实例,然后通过之前的PBQP求解器解决。
Buchwald和Zwinkau也研究和解决了Eckstein等人的PBQP求解器的一些缺陷,由于信息传播不充分,这些缺陷可能会在某个特定场景找不到解法。但是,Buchwald和Zwinkau可以警告说当重叠的模式的数量增长的时候,他们自己的实现无法很好地扩展。
基于处理器建模的方法
在前一章中,我们看到了一种微代码生成的方法,其建模了目标处理器的整个数据链路,而不仅仅只是可用的指令集。这里我们将会关注依赖于相同建模方案但解决了指令选择更传统的问题的技术。
CHESS
在 1990 年,Lanneer 等人[166] 开发了一个方案,其在后来被 Van Praet 等人[249, 250]用在了他们实现的 CHESS 上,这是一个知名的针对 DSPs 和 ASIPs 的编译器,是一个欧洲项目的成果。
将 CHESS 和 MSSQ 比较时 – MSSQ 我们在 4.3.5 节中解读过了– 有两个显著的不同。首先,在 MSSQ 中处理器的数据链路是由手工写的描述文件提供的,而 CHESS 中数据链路是由基于 nML 格式的文件自动生成的[90,91],这减少了人力需求。
第二,打包的方法 – 即合并能并行执行的操作 – 是不同的:在 MSSQ 中,指令选择器依赖于 DAG 覆盖,通过寻找数据路径模型图中的子图来覆盖表达式树,然后在模式选择之后,一个后续的例程尝试调度选择好的指令使其并行化。与之相反的是, CHESS 采用了更渐进的方式,制定了一个链接图,其中每个节点表示表达式图中的一个操作(允许包含循环)。节点由可以执行这个操作的功能单元标注着。在 DSP 处理器上,功能单元通常被分组为功能构建块(FBBs),然后为每对潜在的能在相同的 FBB 中执行的节点对在链接图中添加一条边(这被称为链接)。在然后一个启发式的算法尝试去收缩链接图中的节点,通过选择一条边,接着用一个新节点替换两个节点,然后删除不能在再与新节点的操作在同一个 FBB 上执行的边。这个过程会一直迭代直到没有节点能在压缩的,然后链接图中剩余的每个节点都构成一个包。后来这个作者在 [249] 中扩展了这个方法,通过分支限界搜索在所有可能的包中进行选择,允许表达式图中相同的操作出现在多个包中。
通过链接图逐步构建包的方式,Van Praet 等人的方法能够将整个函数建模为表达式图和跨基本块边界的包操作。它的集成特性也允许为复杂的架构生成汇编代码,让它适合于 DSPs 和 ASIPs 等这类数据路径通常是非常的规律的结构,因为它是基于图的,所以它似乎可以扩展到建模具有内部循环的机器指令。但是,尚不清楚这种方式如何处理相互依赖的机器指令。
模拟退火
另一个尽管不是很常见的技术是由 Visser [251] 提出的。就像 MSSQ 和 CHESS 一样,Visser 的设计是一种集成的代码生成技术,但是应用了模拟退火理论来提高效果。 简单来说,通过将表达式图里的每个节点随机地映射到建模处理器的硬件图里可以获得一个初始的解法,然后使用一个启发式表调度器找到一个调度。应用适应度函数来判断解决方案的有效性–参考论文中省略了确切的细节–然后进行各种修改,以找到更有效、更接近的解决方案。已经开发了一个概念验证原型并在简单的输入程序里验证了,但似乎还没有对这个想法进行进一步的研究。
总结
在这章中,我们研究了许多基于图覆盖的指令选择技术。比起仅在树或者 DAG 上有作用的设计,基于图的指令选择器更强大,因为输入程序和机器指令模型可以采用任意的图形。这也使得可以进行全局指令选择,因为表达式图可以建模输入程序的整个函数,而不只是单个基本块,从而能够产生更高效的汇编代码(如 Eckstein等人展示的)。
但是,图的模式匹配也变成了一个 NP-完全的问题,故而比起 DAG 覆盖只有一个 NP-完全的问题,最优图覆盖需要有两个 NP-完全的问题组成。因此,我们很有可能只会看到这种方法只应用到用户能够负担得起长编译时间的编译器中(如,在性能,代码大小,能源消耗或它们几个的组合上有极高需求的嵌入式系统中)。
结论
在这个报告里,我们讨论、测试和评估了绝大多数不同的指令选择方法。从一体式的指令选择器开始–它是定制的由手工创建的–我们已经看到该领域如何发展为可重定向的宏观扩展设计, 这后来被替换成了更强力的树覆盖。随着形式化方法的引入,从一个声明式定义的目标机器描述自动化生成指令选择器。树覆盖反过来演变成更通用的类型即DAG和图覆盖,但代价是复杂度的增加。因为最优的DAG和图覆盖都是NP完全的问题,所以大部分这种算法都采用启发式来限制搜索空间。同时,也取得了将宏观扩张与窥孔优化相结合的发展,其已经被证明是非常有效的方法,当前还在GCC中被使用。附录 A 给出了所研究方法的易于理解的概述,附录 B 包含一个图表,说明了研究如何随着时间的推移取得进展。
指令选择是一个已解决的问题?
尽管指令选择技术在过去的40年里已经有了巨大的提升,但构成当前最先进技术的指令选择技术仍然有几个显著的缺点;最值得注意的是,没有方法–至少在我已知–能够对具有内循环特征的机器指令进行建模。今天,虽然可以通过客制化路由识别何时特定的机器指令可以被利用来削弱这个影响,但这是一项容易出错且实施起来繁琐的任务。更灵活的解决方式是使用编译器固有函数–其可以被看作是表达式图里额外的节点类型,它可以表达更复杂的操作如$\sqrt{x}$ – 或者调用目标架构特定的库函数–其是直接用汇编指令实现来执行特定操作的。但是,这并不理想,因为通过额外的固有函数扩展编译器来获得新的指令集的优势通常需要大量的人力成本,且库函数需要为每个目标机器都手写一版。
此外,正如我们在简介中所述,必须同时考虑代码生成的所有三个方面,以便生成真正最佳的汇编代码。由于多种原因,孤立地选择最佳指令是徒劳的:例如,在没有将指令调度纳入考虑的时候,是无法更高效地使用条件码的(或者标志位,因为它也可以被这样讲),因为我们需要保证标志不会过早地被另一条指令重写掉。VLIW 架构也是如此,其中多个机器指令可以捆绑并并行执行。另一个问题是重物化,它意味着不是将值保存到寄存器里直到它被使用,而是在使用的时候重新计算。如果目标机器只有比较少的寄存器,或者溢出成本非常的高,则这会是一个非常有效地提升代码质量的方法。但是,只有当重物化实际辅助寄存器分配,或者只有很低开销的时候(如,利用并行执行),它才有收益。对于带有多个寄存器类型的目标机器,即访问不同的寄存器类型都需要特定的指令,指令选择和寄存器分配之间的联系变得更加紧密。
话虽如此,大多数当代技术仅单独考虑指令选择,并且通常不清楚它们是否可以与指令调度和寄存器分配完全有效地集成。
从这里到哪里去?
尽管存在这些问题,但是基于组合优化方法的技术–即,整数规划,约束规划,SAT等,这个报告里包含了一些例子包括Wilson等人【263】,Bashford和Leupers【28】,Bednarski和Kessler【29】以及Floch等人【197】–已经表现出一些希望了:首先,底层的建模机制促进了一个集成式的代码生成方法;第二,辅助的约束经常可以被添加到已经存在的模型里,因此允许使用相互依赖的指令而不需要采用手写汇编或者客制化优化例程;第三,求解器技术的最新进展使这些技术成为代码生成的可行选择(参见Castañeda Lozano等人的方法【43】)。但是,现在的实现比起启发式的方式,仍然慢了一个以上的数量级,表明这些想法还需要进一步研究。
综上,虽然指令选择这个领域从19世纪60年代就开始初步的尝试了,但是它仍然–尽管有些共识–是一个重要的问题。而且,当前的趋势是集成式代码生成和日益复杂的目标机器,因此与之前相比更需要深入理解指令选择。