自动存储优化
简介
高级语言的大部分优化技术研究关注于改善生成的程序的执行时间,通常以增加储存为代价。当解决了存储优化之后,通常也会影响到时间类的优化,例如指令减少相关的代码转换。在 Bliss 编译器(WJWHG75) ,这样一个存储优化编译器中,也会执行降低寄存器临时存储的转换,但是没有解决程序变量自动覆盖的问题。
微型计算机和微处理器的日益普及表明,到了全面检验自动存储优化问题的时候了。因为在小型系统的环境下,缺少空间总会是一个问题,小型机器的普及意味着这个问题的重要性日益增加。虽然内存成本的下降会减缓这个趋势,但是墨菲定理的一个变体确保了程序大小的增长总是快于可用内存的增长。换句话说,程序员总是写不合适的程序,因此,随着时间的推移,他们会做得更多。
即使小型计算机的时代没有到来,但从语言的角度来看,这样的调查还是有必要的。几乎所有的编程语言都在变量的概念中包含了存储的概念,它们的编译器将变量以一对一的方式映射到存储中。节省内存的程序员,使用没有内存等效特性的语言,需要特意将单个变量用于多种用途中。无论哪种方式,程序的明晰性和可靠性都会受到影响。一个理想的替代方案是,语言中的变量没有内存的意义,但是处理器会进行所有变脸的内存分配决策,保证变量的完整性。这是个重要的目标,因为,不像时间相关的代码优化技巧的范围是相对局部的,一个存储类的代码优化技巧通常能覆盖整个程序。
PL/1 等语言的数组和字符串临时变量在编译器中的管理也需要用到自动覆盖技术。
存储优化在虚拟存储系统中也有应用,其降低了程序大小可能会让对象程序需要的页更少,从而在执行时间上有一个提升。Kernighan(K71)已经处理了以最小化页间跳转的方式来组织给定大小的程序的相关问题。另一个相关的问题,是将变量分配给几个内存类之一,从而使得总变量访问开销最小,这是由 Warren(W78)解决了。
本文的目标是划定一些存储优化编译器设计涉及的一些基础问题,然后介绍这种编译器中使用到的算法和技术。下一节中,将自动覆盖问题规范为扩展的图着色问题,然后讨论存储优化问题公式的影响。给出扩展颜色数量的上下边界。
这个扩展着色公式有助于提出设计覆盖启发式的方案。第 3 节描述了迄今为止产生的有出色实验结果的覆盖算法。
扩展着色公式为存储优化的代码变换提供了一个框架。在后续的章节中,给出了一个规范的重命名变换,其通过引入新的变量来承担旧变量的一些冲突,从而提高数据覆盖机会,不过需要精确地确定新旧变量之间移动的位置。这种变换对于寄存器优化也是重要的,因为它可以精确地确定寄存器移动操作需要插入的位置,从而降低需要的寄存器数量。
许多的时间优化转换,如代码移动和冗余代码消除,以及它们的反操作,可以被用于提高自动覆盖的机会。这几个例子由第 5 节的例子展示。
前置准备
给定一个程序流图(NDS,EDGS),以及一组变量 VARS。程序节点可能是低级别三元组,高级别语言语句,基本块,过程块,或者任意被视为当前分析的基本单元。与任意变量 V 关联的是它声明的大小 $|V|$。对于 VARS 的任意子集 SV,SV 的大小,\SV\,是 SV 中变量大小的和。
一个复合类型 V 的子引用 S 被定义为 V 的标量元素的一个特殊集。一对 V 的子引用可能是不相交的(即,指向 V 的不同标量元素)或者联合的(即,不是不相交的)。编译器使用从范围分析得出的信息可以确定一个变量的子引用(Ha77)。缺失这些信息,则变量的子引用只能是它自己。
我们将引用的定义和引用的修改区分开,因为前者会导致引用中的所有元素的值都发生了变化,而后者只会导致引用中的部分元素的值发生变化。范围信息可以识别出定义赋值,如当一个下标数组被赋给一个覆盖整个数组的循环。需要注意的是,除非有相反的信息,否则必须假定这样的赋值就是修改。
当程序流图中有一条路径不会穿过(V,S)任意定义或者任意联合,且这条路径中的节点 I 到节点 J 会使用到(V,S)或者它联合体中的一个时,一个引用(V,S)在节点 I 退出时被认为是有效的。需要注意的是,如果缺少范围信息,一个引用必须假定总是在节点中存活的,即使事实上它已经失效了,因为之前的一些赋值被认为是修改而不是定义。
如果一个变量 V 的任意引用时存活,使用或者修改(或定义),则它被称为在节点 I 中处于活动状态。节点 I 中的活跃变量的集合被表示为 ACT(I)。粗略地说,ACT(I)是必须在节点 I 中保留存储的变量最小集。LNACT(V)表示变量 V 存活的节点集。
不兼容图 IG 的概念,是 Yershov(Y71)引入的,它是自动存储优化的核心概念。IG 中的节点相当于 VARS 的元素。每个节点关联一个权重,其相当于变量的大小。如果 NDS 中的一些节点 I ,有 X 在 ACT(I)中,Y 在 ACT(I)中,则边(X,Y)在 IG 中。因此,一条边连接一对节点,当且仅当变量同时处在活跃状态,因此不能共享存储。
现在,我们看到着色和色彩数量的概念可以扩展,从而着色对应于存储布局,色彩数量对应于存储布局的最小数量。对于权重图中的每个变量 V,一个着色 COL 将 V 映射到一个整数区间,它的大小是 V 的重量。如果 (V,V1)是图中的一条边,则COL(V)和COL(V1)不能重叠。
对于一个特定着色 COL,着色的值,VALUE,是区间中最右侧位置的所有节点的最大值。一张权重图 G 的扩展色彩数量 CHR(G)是 VALUE 的所有可能的着色 COL 的最小值。
为了找到特定权重图的 CHR,必须探索所有的区间着色。附录(F79)给出了一个精确地覆盖算法。因为简单的图着色是已知的 NP-完全 问题,自动数据覆盖是明确需要一个启发式规则的。不幸地是,Garey 和 Johnson(GJ76)给出的结果表明,对于简单的图着色,任意多项式渐进算法都会在某些图上产生任意差的结果。因此,我们最大的希望是,不兼容图有一些独特的,正则的属性,可以被特定的启发式利用。
这里我们会提到但不推行的,一个可能的方式是,对可能作为不兼容图出现的权重图的特定子类进行搜索。特别是,对一个直线程序的不兼容图的着色问题,等价于 Shipbuilding 问题,这个问题 Hoffman,Johnson,Stockmeyer,和 Golumbic(HJSG77/8/9,G79)已经调查过且被证明是一个 NP-完全问题。不知道一个多项式渐进算法是否可以在这种类型的图上演示,或者说 Garey/Johnson 的结果是否也适用于此。
对于存储优化的兴趣,除了寻找一个有效着色启发式,我们也寻找降低 CHR(IG)的方法。因为,这似乎很困难,如果不可能,则我们可以寻找降低色彩数量下界作为替代方案,这是一种可能会减少过程中色彩数量的方法。
我们将 |ACT(I)| 的所有活跃集合 ACT(I)的最大值定义为 MAXACT。MAXACT 明显是 CHR(IG)的下界。
一个团是图 G 中的一个子集 C,C 中的任意两个节点两两相连。一个团的大小是团中节点的权重和。如果 CLIQS(G),G 中的团集合,被测试,大小最大的团被称为“最大团”,且它的大小被称为最大团大小MC(G)。因为根据定义,团中没有节点对是共享存储的,则最大的团大小同时也是扩展色彩数量的下界。
请注意:
$$
MAXACT <= MC(IG) <= CHR(IR)
$$
例如,如果 X,Y,和 Z 不会同时活跃,但如果 X 和 Y 在同一个节点集中活跃,Y 和 Z 在不同的节点集,且 X 和 Z 在第三个节点集,则三个节点会来自 IG 的一个团,需要为每个变量都预留一个存储位置。最后,MAXACT 可能会小于 MC(IG)。在第 4 节中,我们会看到程序总是可以被转换,使得 MC(IG)减少到 MAXACT。
Chaitin(C79)提出了 Yershov 公式的改进点 。他观察到,在一个中间语言程序中,一对标量 X,Y 在实际中会冲突,当且仅当在某个节点 I 处定义了 X,并且 Y 在退出时处于活跃状态。 该公式允许最后一次使用与第一次定义重叠。
为了使得这里考虑的任意程序节点可以适配这个改进,我们说在节点 I ,X 与 Y “冲突“,只要 Y 在节点 I 存活同时 X 在节点 I 被修改。(需要注意到这不是一个自反关系,且需要节点中冲突模式的信息。)
我们定义 CON(I)为节点中冲突变量对的集合。在每个程序节点 I 中,一张局部冲突图 LCG(I)是由 CON(I)归约的边形成的,MC(LCG(I))是 LCG(I)中最大的团大小。MAXLOC 定义为 MC(LCG(I))的所有节点 I 上的最大值。
冲突图 CG 是由所有程序节点 I 的 CON(I)归约的边形成的。可以看到 CG 总是 IG 的子图。
$$
MAXLOC <= MC(CG) <= CHR(CG)
$$
因此,MC(CG)是所需要的覆盖存储的下界。在第 4 节中,我们将会看到程序总是可以转换,从而 MC(CG)可以被归约成 MAXLOC ,而不增加 CHR(CG)。
探索扩展色彩数量上界的存在也是有用的。Brooks 证明了普通色彩数量的上限为 1 + MAXD,其中 MAXD 是图上所有节点的 DEGR(V)的最大值,其中 DEGR(V) 表示节点 V 的度。这个结果被 Szekeres 和 Wilf(SW68)进一步强化了,通过将 MAXD 替换为:G‘ 中的 V 上的 DEGR(V)的最小值的 G 的所有归约子图 G’ 上的最大值。
不幸地是,这些定理不能一概而论。如果将节点的扩展度定义为相交边的权重和,就会给出一个反例。但是,Hoffman(H78,F79)使用了一个不同的定义,证明了一个最新的上界:
$$
EXTDEGR(V) = |V| + \sum\limits_{在 EDGS 中的(V,W)}(|V| + |W| - 1)
$$
Hoffman 的结果对存储优化具有重要的意义,因为现在,尝试降低扩展色彩数量的启发式可以专注于降低上下界的转换。
覆盖启发式
Yershov(Y71)将覆盖确定问题作为着色和包装问题,然后使用不兼容图来解决它。Yershov 观察到如果所有的变量都有相同的大小,覆盖确定问题则会完全等价于简单图着色问题,则剩余的工作变成寻找一个高效的着色启发式。因为涉及到不同大小的变量,执行某些打包功能的第二启发式,不得不与着色启发式结合在一起。
为了证明这个方法,Yershov 假设了一个“均匀性原则”,断言大多数的程序有数据变量的同一集,因此,标量,数十个存储单元大小的数组,上百个存储单元的数组等都需要相当数量的存储。他的方法是使用着色启发式,尽可能多的覆盖近似相同权重的变量,然后用更小的数组“打包”更大的数组。
Yershov 的方法有一些缺点。他的着色算法并非专门为不兼容图高效设计的,而是依赖于“两个节点距离”的启发式。如果统一原则不适用,内存利用率会相当低。而且,覆盖只会发生在一个可覆盖变量的边缘,经常浪费可用的存储。例如,Yershov 的启发式无法产生如下的覆盖结构:
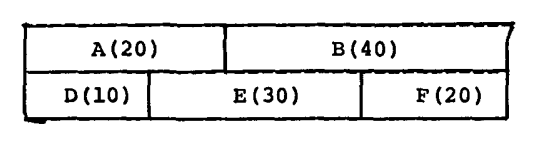
如果 D 可以只覆盖 A,F 可以只覆盖 B,但 E 可以覆盖 A 和 B,则 Yershov 的方案总会导致 20 个单元的浪费。
Logrippo(L78)提出了一个重命名的方案来进行自动覆盖决策,它也有最后两个缺点。
一个有希望的冲突图着色方法是 Ashok Chandra(CCC77) 提出的回溯着色算法。这个算法使用紧迫性测量启发式来选择要着色的节点。这个启发式在无权重冲突图上效果很好,它几乎不需要回溯重新着色节点。这表明冲突图会有些属性,让其可以满足这个启发式。在为扩展着色近似算法适配这个方法的过程中,我们观察到:
- 对于一个节点 X,当前可用的区间总大小越小,能选择的区间自由度越低,因此,接下来分配 X 就越紧迫。
- X 当前的度越大,下次分配 X 的可能性就越大,剩余未着色的节点能实现更多区间共享的机会。
这个方法根据测量得到的顺序来选择节点,然后使用一些存储分配策略,如首次满足,最佳满足,或者局部回溯技术,来为变量选择区间。从图中移除这个节点,然后更新相邻节点的品质因数。重复这个过程直到所有节点都被更新了。
这一系列的启发式规则和首次满足策略(F29)一起被实现和测试了。132 个小图中有 82% 获得了最佳结果,其中有 97% 有 20% 的优化。
重命名转换
重命名是一种降低最大团大小的方案。重命名转换给程序引入新的变量,来承担旧变量的一些冲突,然后精确地确定新旧变量之间移动的位置。这会打碎冲突图中的团,因而 MC(CG)最终降低到 MAXLOC,而不会增加 CHR(CG)。事实上,CHR(CG)通常都是由这个转换降低的。重命名还会破坏不兼容图中的团,将 MC(IG)降低为 MAXACT,且通常减少 CHR(IG)。
这个结果对于寄存器优化也是重要的。寄存器优化对应于简单图着色问题。规范重命名转换将 MC(CG),所需寄存器的下界,降低到 MAXLOC,任意特定节点需要的最大寄存器数量,然后精确地决定需要插入“移动-寄存器”的位置。
当几个节点间的不同变量间冲突的聚合产生一个更大的变量间冲突时,重命名是适用的。例如,考虑如下的 PL/1 程序段:

对于这个程序,活跃集 {ACT(I)}是:
{A,B}
{C,A}
{C,B}
冲突对 {CON(I)}是:
{(A,B),(B,A)}
{(C,A)}
{(C,B)}
IG 和 CG 组成团 {A,B,C},MC(IG) = MC(CG) = 80,MAXACT = MAXLOC = 60。
重命名变换的核心,变换 R,定义为如下方式:假设 X 和 Y 同时属于 CLIQS(G)中的某些团 C,|C| = MC(G),其中 G 是 IG 或者 CG。如果,不失一般性的,G 是 IG,我们需要 |X| <= |Y|。如果 NBOTH 不为空,则 R 适用,定义如下:
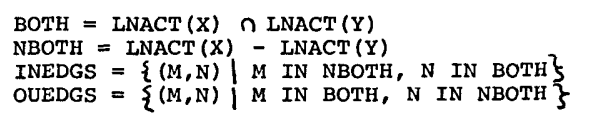
注意到 INEDGS 和/或者 OUEDGS 可能是空的。变换 R 导致引入新的变量 X_Y,有 |X_Y| = |X|。程序以如下方式修改:
步骤 1. FORALL N IN BOTH:
用 X_Y 的引用替换每个到 X 的引用。
步骤 2. FORALL (M,N)IN INEDGS:
在 M 和 N 之间插入一个包含以下语句的节点:X_Y := X;
步骤 3. FORALL (M,N)IN OUEDGS:
在 M 和 N 之间插入一个包含以下语句的节点:X := X_Y;
如果在前面的示例中对(B,C)对应用了变换 R,则会构建如下的集合:
BOTH = {L5,L6,L7 }
NBOTH = {L1,L2, L4}
INEDGS = {(L4,L5)}
OUEDGS = {}
以下是程序结果:

新的活跃集 {ACT(I)} 是:
{A,B}
{C,A}
{B_C,B}
{C,B_C}
新的冲突对集合 {CON(I)} 是:
{(A,B),(B,A)}
{(C,A)}
{(C,B_C)}
IG 由边(A,B),(A,C),(B_C,B)和(B_C,C)组成,且 MC(IG) = MAXACT = 60。CG 由边(A,B),(A,C)和(B_C,C)组成,且 MC(CG) = MAXACT = 60。两个场景中,B_C 可以覆盖在 A 上,B 可以覆盖在 C 上,所有 CHR(IG)= CHR(CG)= 60。
在引文(F79)中,它证明了重复应用变换 R 可以将 MC(IG)降低到 MAXACT。可以证明用相似的方式重复应用,能把 MC(CG)降低到 MAXLOC。此外,因为 X 和 X_Y绝不会相互冲突,所以显然 CHR(CG)将不会增加。事实上,CHR(CG)和CHR(IG)通常可以用重命名降低。
重命名也可以用于分开冲突图中的其它团。变换 R 能应用到一个团上,只要团中的一些元素对的 NBOTH 是非空的。
其它变换和技术
在编译器中,在应用自动覆盖技术的前后,都可以尝试存储优化代码变换。在前一个场景中,通过消除一条边或者降低节点的大小,目标是为了降低最大大小的团或者扩展特定节点的度。在覆盖之后,覆盖的结果可以用于查明哪些变量的大小降低了,或者消除了哪些冲突的变量对。
Allen 和 Cocke (AC72)编写了一个时间类优化代码的目录。根据情况,许多这样的变换可以提高或者禁止自动覆盖的机会。在这节中,我们考虑一些例子。
某些情况下,比起适用存储来保留不相邻使用间的值,如果重新计算一组值,可以更有效地共享存储。下面的例子解释了这个观点:

冲突对集合:
{(B,A)}
{(C,A),(C,B)}
{(D,A),(D,B),(D,C)}
{(E,A),(E,C),(E,D)}
{(G,A),(G,C)}
{(H,G)}
下面的存储布局是这个程序最好的:
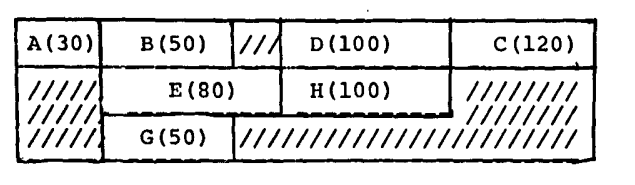
共:330
在 C 第二次使用的时候,重新计算 C ,放入重命名的变量中,我们获得了如下程序:

冲突对集合是:
{(B,A)}
{(C,A),(C,B)}
{(D,A),(D,B)}
{(E,A),(E,C),(E,D)}
{(C1,A)}
{(G,A),(G,C1)}
{(H,G)}
现在,可以实现下面的赋值,节约了 70 个对象存储单元,代价是指令存储和程序执行时间。
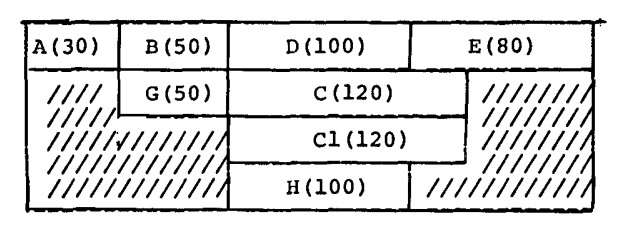
共:260
虽然这个例子中插入冗余代码增加了覆盖机会,但是在其它情况下,消除冗余代码也会产生这种效果。代码移动也可以提高利用率。考虑如下的例子:

冲突对集合如下:
{(B,A),(C,A),(C,B)}
{(D,A),(D,B),(D,C)}
{(K,A),(K,B),(K,C),(K,D)}
{(E,B),(E,C),(E,D),(E,K)}
{(G,C),(G,D),(G,K)}
{(H,G)}
就目前而言,如下存储赋值时当前程序能做到的最好的情况了:
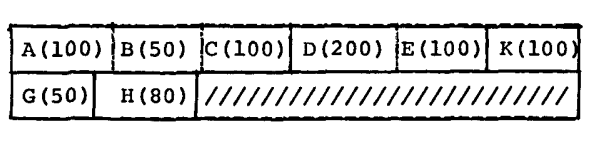
共:650
如果语句 6 向上移动了两个语句,就会有如下的存储覆盖改进的可能,它产生了 20个单元的节省:

新的冲突对是:
{(B,A),(C,A),(C,B)}
{(D,A),(D,B),(D,C)}
{(K,A),(K,B),(K,C),(K,D)}
{(H,A),(H,B),(H,D),(H,K)}
{(E,B),(E,H),(E,K)}
{(G,H)}
对应的新的存储布局是:
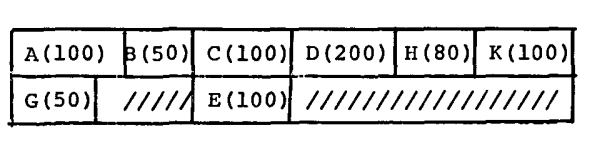
共:630
存储优化线性代码排序问题,在线性代码段中寻找一个语句顺序可以最小化 CHR(CG)的问题,可以被视为寄存器优化线性代码顺序问题的带权重泛化,这个问题 Sethi (S75)已经证明是 NP-完全的了。Aho,Johnson,和 Ullman(AJU76)已经研究了非权重问题的启发式。
循环拆分,在 Allen-Cocke 目录中(AC72)讨论了逆“循环融合”变换,对于暴露冗余代码插入和代码移动机会是有帮助的。进一步的改进通常可以通过循环融合和降级来实现。考虑如下的例子:

这个程序需要 203 个单元,且没有覆盖的可能。但是,如果循环和前两个节点拆分开,代码就可以重新排序,从而需要的储存就减半了:

现在,A 和 B,SUMA 和 SUMB,I 和I1都可以共享村粗。下一步通过循环融合和降级可以实现更多的存储节省。如果每个隐式的输入循环都可以和后继计算循环融合,每个数组的秩都可以降低,则有如下程序:

现在只需要三个字的数据存储。
数据溢出是冗余代码插入的替代方案。虽然它经常用于寄存器优化中,其寄存器内容溢出到存储的开销是可以接受的;但是,它也可以用于存储优化,虽然将变量放入两个使用之间的辅助存储,和在需要的时候恢复到重命名的变量的开销,会更高。这个技术的自动化关键在于时间和空间的平衡。
数据碎片化是另一个优化技术。比起连贯的变量,覆盖启发式通常可以更优化地分配碎片化的变量。变量不相交的子引用和覆盖启发式的结果可以用于确定一个分段。
存储优化不局限于数据存储。覆盖启发式也可以用于管理指令存储。代码可以分割成块,然后每个块可以被覆盖启发式视为一个变量。
当合并分离的过程时,可以执行过程间覆盖。一种方式是当一个过程被编译时,为局部变量执行覆盖;当过程被融合的时候,覆盖结果段。对于非递归的过程,另一种方式是,为整个程序产生一个巨大的冲突图,在每个调用点将局部变量作为重命名变量。中间的方法也是可行的。
在引文(F79)中,会更细致地讨论存储优化代码变换和它的实现。
结论
本文中,描述了自动存储优化的基本问题。数据覆盖被设定成扩展图着色问题。提出了扩展色彩数的上界和下界,因此存储优化变换的目标就是降低它们。然后引入了一个有效且高效的覆盖启发式。
一个规范的重命名变换已经被证明可以尽可能地降低冲突图的扩展色彩数。也通过例子图解了一些其它的存储优化变换。
一个名为 SOCRATES 的实验研究,即存储优化,代码重组织和变换实验系统,已经初始化了,调查了本文中描述的变换和技术对于实际程序的适用性。引文(F79)讨论了实现细节和初始结果。
自动存储优化是编译器技术中一个相对未开发的领域。其中一些算法的实际实现仍然有待研究,特别是对于在小型机器上运行的编译器。
引用
略。