LALR高效计算-向前看集
定义了两种关系,用于捕获LALR(1)向前看集计算问题的基本结构;以及给出了计算这个集合的高效算法,其是与关系大小相关的线性时间。特别的,对于一个 PASCAL 语法,这个算法的执行性能比通过通用编译器-编译器 YACC 执行这个集合单元小 15%。
当一个语法不是 LALR(1),显式给出的,关系,提供给面向用户的错误消息,其特别给出了向前看问题是怎样出现的。此外,由这些关系导致的有向图中的某些循环表明对于任意 k,这个语法不是 $LR(k)$。
最后,一个经常被发现和使用,但不正确的向前看集合算法同样基于这里第一次定义的另外两个关系。这个算法的形式化定义应该有助于防止重复发现它。
简介
因为 DeRemer [9] 发明的 LALR(1)语法,LALR 语法分析和解析技术作为翻译书写系统和编译器-编译器的一部分变得流行开了。但是,DeRemer 没有描述如何计算所需的向前看集合。反而,LaLonde 是第一个给出算法的[20]。在这之后,LaLonde 的算法由 Anderson 等人发表,[6, pp. 21-22],他们也给出了他们自己的算法[6, pp.21];Aho 和 Ulman[3, p.238] 给出了 YACC 使用的算法[16]。Kristensen 和 Madsen[19] 改善了 LaLonde 的算法,将结果扩展到了 $LALR(k)$。
许多人也尝试过设计这种算法,通常是实现了 LALR(1)的特定子集,我们称之为“不完全的” LALR(1)或者 NQLALR(1)[7, 11, 23, 25]。随后,Watt 尝试重复他原始的方法 [24],和 Chaney 与 DeRemer 的方法相同 [5]。这些后来的尝试都是不正确的,虽然比起 NQLALR 方法,两者更复杂,适合更多的场景。
基本没有正确的 LALR(1)算法,除了 Kristensen 和 Madsen [19, Sec. 6.2],几乎和他们的 NQLALR(1)同行一样高效。然后我们描述简单的简化这个结果,高效的算法不是完全正确的。当前论文的目的是提供一个算法,可以高效地利用问题的本质结构。
回顾
当一个文法不是 LR(0),一个或多个 LR(0)解析器的状态必然是“不一致的”,有“读-下降”或者“下降-下降”冲突,或者两者都有。在前一种情况下,解析器无法决定是否是去读下一个输入的符号,或者去减少栈中的一个短语。而在后一个场景中,是两个明显的下降的困惑。在输入的第一个符号向前看可能会解决这个冲突,因此 DeRemer 定义了一个文法为 LALR(1),每个不一致的状态 q 可以通过向前看集增强,可以解决冲突,得到一个正确的,确定性的或者“一致”的解析器[9]。
更确切地说,对于每个不一致的状态 q 和 q 中可能的下降 $A\rightarrow \omega$,令 “$A \rightarrow \omega$ 的前瞻集” 表示为$LA(q, A\rightarrow \omega)$。当解析器处于状态 q,以及在输入的头的符号是在 $LA(q, A\rightarrow \omega)$,则 $\omega$ 必须下降到 A。因此,q 中的向前看集必须是不相交的,且不包含任意可以从 q 中读取的符号。
Watt [24] 已经定义了$LA(q, A\rightarrow \omega)$ 作为 ${t\in T | S\Rightarrow^+\alpha Atz\ 和\ \alpha \omega 访问 q }$,其中 T 是语法中的终止符集合。直观地,当解析器处在状态 q ,$\alpha \omega$ 在栈上时,要是输入是以一些遵循$\alpha A$最右侧句子的形式的终止符 t 开始的,则$\omega$ 到 A 的归约是刚好的。这边我们的目的是调查这个定义潜在的结构,从而表明如何更高效地计算 LA。
这个问题可以分解为四个独立的计算式。以相反的计算顺序,它们如下:LA 计算自非终结符转换的“Follow”集;Follow 集由非终结符的“Read” 集计算;Read 集由 “Direct Read” 集计算;Direct Read 集合由检查 $LR(0)$ 解析器计算。
定义了一个非终结符转换关联 Follow 集的关系 includes,伴随着关系 Reads 关联 Read 集。通过解析器的检查,Read 集初始化为 Direct Read 集。然后,他们的值由一个图转换算法完成,为了找“强连通分量”(SCCs),适用于当它搜索由 reads 关系导出的有向图时,适当地计算集合的并集。如果找到一个非平凡的 SCC,问题中的语法对于任意的 k 都不在是$LR(k)$。下一步,Read 集 作为 Follow 集的初始值使用,通过在 includes 关系的有向图上应用 SCC 算法完成。再次,如果遇到的非平凡 SCC 中有一个非空的 Read 集,则(我们推测)这个语法对于任意的 k 都不是 $LR(k)$。在任意的场景中,LALR(1)向前看集是适当 Follow 集的简化合集。
现在我们定义术语,定义 LALR(1),给出向前看集计算的相关定理,给出算法,简化讨论,给出一些实际语法的统计数据,表明如何为不是 LALR(1)的语法生成调试诊断,给出结论。
术语
这里假定了符号的概念和符号串。一个词汇 V 是一个符号集。$V^*$ 表示符号的字符串集合全部来自 V。$V^+$ 表示$V^* - {\epsilon}$,其中 $\epsilon$ 是空字符串。任意字符串$\alpha$ 的长度表示为$|\alpha|$。一个非空字符串 $\alpha$ 的第一个符号由 $First\ \alpha$ 表示;剩余的字符串由 $Rest\ \alpha$ 表示;最后的符号由 $Last\ \alpha$ 表示。如图所示,当意图明显的时候,给函数的参数是不带括号的。
如果 $R$ 是关系,$R^*$ 表示 R 的自反的,传递闭包,然后 $R^+$ 表示传递闭包。我们写 $X =_s F(X)$ 意味着 X 是满足$X = F(X)$ 的最小集。$\cup{S_1, …, S_n} $,其中 $S_i$ 是集合,表示$S_1 \cup … \cup S_n$。
CFGs
一个上下文无关语法(CFG)是一个四元组$G = (T, N, S, P)$,其中 T 是一个终结符的有限集,N 是一个非终结符符号的集合,$T\cap N = \empty, S\in N$ 是起始符号;P 是 $N \times V^*$ 的有限子集,其中$V = T \cup N$,每个成员称为一个产生式,写为$A\rightarrow\omega$。$A$ 称为左侧部分,$\omega$ 称为右侧部分。我们需要一个产生式$S\rightarrow S^{‘}\bot$,对于一些 $S^{‘}\in N $ 和 $\bot \in T$,如此$\bot$ 和 $S$ 不会出现在其它产生式中。
本文采用以下(通常)约定:
$$
S, A, B, C, … \in N
$$
$$
X \in V
$$
$$
t, a, b, c, … \in T
$$
$$
…, x, y, z \in T^*
$$
$$
\alpha, \beta, \gamma, … \in V^{*}
$$
关系 $\Rightarrow_r$ 读作“直接(右)产生”以及定义在 $V^*$,有 $\alpha Ay \Rightarrow_r \alpha \omega y$ 满足所有的$\alpha \in V^*, y \in T^*$,和$A\rightarrow \omega \in P$。下标 r 之后会丢弃,因为我们总是说右表达式。$\Rightarrow^*$ 和 $\Rightarrow^+$ 读作产生。一个可为空的非终结符式一个产生$\in$。如果$S \Rightarrow^* \alpha$,则 $\alpha$ 是一个句子结构;如果$\alpha \in T^*$,则它称为一个句子。由 G 生成的语言 $L(G)$ 是句子的集合,即,${x\in T^* | S \Rightarrow^+x}$。这里的语法假设都是可归约的,即对于所有的 $A\in N$和 一些$\alpha, \beta 和y\in V^*$, 有 $S\Rightarrow^+ \alpha A \beta$ 和 $A \Rightarrow^* y$ 。
令 G 是 一个 CFG,$k \geq 0$。G 是$LR(k)$ 当且仅当 $S\Rightarrow^* \alpha Ay \Rightarrow \alpha \omega y$ 隐含着,如果 $S \Rightarrow ^* \gamma \Rightarrow \alpha\omega y^{‘}$ ,则对于所有的$\alpha, \gamma \in V^* 和 y, y^{‘} \in T^*$,有$\gamma = \alpha A y^{‘’}$,因此$First_k(y^{‘}) = First_k(y)$ [17]。这里 $First_k(y)$ 是 $y$ 的 $k$ 长前缀,或者只有 $y$ ,此时$|y| < k$。
LR 解析器
下一步,我们介绍一个 LR 解析器的形式化,即,一个任意单符号向前看解析器,如,SLR(1),LALR(1),或LR(1) 解析器[1]。然后扩展都多符号向前看集是比较简单的,但这里不在涉及。给出一些下面定义的“LR 自动机”表格表示,和通用的 LR 解析算法解析那些表,我们有一个“LR 解析器”。特定的状态,转换,和向前看集由问题中的语法和结构化技术定义。例如,LALR(1)技术产生一个“LALR(1)自动机”。
对于 CFG $G = <T, N, S, P>$ 的 LR 自动机是一个六元组$LRA(G) = <X, V, P, Start, Next, Reduce>$,其中 K 是有限状态集,$V$ 和 $P$ 是在 G 中的,$Start \in K$ 是开始状态,Next:$K \times V \rightarrow K$ 是转换函数,Reduce:$K \times T \rightarrow 2^p$ 是归约函数。Next 可能是个局部函数。非确定性或者“不一致” LR 自动机是允许的;第三节的 LALR(1) 状态去掉了这种场景。一个转换是 $K \times V$ 的一个成员;如果它是在 $K\times T$ 中,则它是一个终结转换;如果它在$K \times N$ 中,则它是非终结转换。转换$(q, X)$ 表示为$q \longrightarrow ^X p$,其中$p = Next(q, X)$;或者当 q 是无关紧要的,表示为$q \longrightarrow ^X $。我们定义接受字符$p = X$。每个状态有唯一的访问字符,除了 Start,其是没有的。
在文本的图表中,LR 自动机由状态图表示,其中状态由转换连接。对于 Reduce 中的每个状态 q 表明了可能的归约,列出了产生式。
一条路径是一系列状态 $q_0, …, q_n$ 如
$$
q_0 \longrightarrow ^ {X_1}q_1 -\cdots\rightarrow q_{n-1}\longrightarrow^{X_n}q_n.
$$
我们说 H 拼出 $\alpha = X_1 \cdots X_n$,定义 $Spelling\ H = \alpha$ 和 $Top\ H = q_n$。H 表示为$q_0 - \cdots ^\alpha \rightarrow q_n$,读作 “$在 \alpha 之下,q_0 到 q_n $”。H 的替代符是$[q : \alpha]$ 和 $[q’ : \alpha’]$,其中 Top $[q:\alpha] = q’$,写作$[q:\alpha][q’:\alpha’]$,表示为$[q:\alpha\alpha’]$。$[Start:\alpha]$ 可以缩写为$[\alpha]$;因此$[\ ]$ 单独表示 Start。如果 $Top [\alpha] = q$ ,我们说 $\alpha\ 接受\ q$。
一个配置是$K^+ \times T^+$的一个成员;它的第一部分是状态检查,第二部分是输入。配置中的关系 $\vdash$ 读作“直接移到”,它是$\vdash_{read}$ 和$\vdash_{A\rightarrow\omega}$ 的并集,对于所有的$A\rightarrow \omega \in P$ 成立。$\vdash_{read}$ 读作“读到”:如果定义了 $Next(Top[q:\alpha, t])$,$[q:\alpha]tz \vdash_{read}[q, \alpha t]z$。$\vdash_{A\rightarrow\omega}$ 读作“归约 $\omega$ 到 A 的移动”:$[q:\alpha\omega]tz \vdash_{A\rightarrow\omega}[q:\alpha A]tz$,当 $A\rightarrow\omega\in Reduce(Top(q:\alpha\omega), t)$(且当$[q:\alpha A]$ 在路径上;但是这个额外的限制总是在当前的 LR 自动机的考虑中)。$\vdash^*$ 和 $\vdash^+$ 读作“移到”。由$LRA(G)$ 解析的语言 $L(LRA(G))$ 必须于$L(G)$ 是相同的,是${z\in T^* | [\ ] z \vdash^+[S’]\perp}$。
一个三元组$(A, \alpha, \beta)\in N\times V^*$叫作一项,写为$A\rightarrow\alpha \cdot \beta$,如果$A\rightarrow \alpha \beta$ 是产生式;如果$\beta = \epsilon$ ,它是终结符。一个项集叫作一个(解析)表。对于一个 CFG 的 $LR(0)$ 解析表 $PT(G)$ 的集合是
$$
PT(G) =_s {Closure{S\rightarrow\cdot S’\perp}} \cup {Closure IS | IS \in Successors IS’ 对于IS’ \in PT(G)}
$$
其中:
$$
Closure IS = IS \cup {A \rightarrow \cdot | B \rightarrow \alpha \cdot A \beta \in IS 和 A \rightarrow \omega \in P}
$$
$$
Successors IS = {Nucleus(IS, X) | X\in V}
$$
$$
Nucleus(IS, X) = {A\rightarrow \alpha X\cdot\beta | A \rightarrow\alpha\cdot X\beta \in IS}.
$$
一个 CFG G 的 LR(0)自动机是一个 LR 自动机 LRA(G),这样存在一个双射函数$F:K\rightarrow PT(G) - {\empty}$,其中
$$
Start = F^{-1} (Closure {S\rightarrow \cdot S’\perp})
$$
对于所有的$t \in T, X \in V$,
$$
Next(q, X) = F^{-1}(Closure(Nucleus(F q, X)))
$$
$$
Reduce(q,t) = {A\rightarrow\omega | A\rightarrow \omega \cdot \in F q}.
$$
F 简单地建立表(除了 $\empty, “陷阱表”$)和状态之间的一一对应,因此解析表和解析器之间是同构的。因此,以后我们省略$F$ 和 $F^{-1}$ 的所有事件, 因为上下文总是决定 q 是否表示一个状态,它关联的解析表。自动机的“LR(0)度“的是明显的,因为 $Reduce(q, t)$ 的定义是独立于 t 的。以后,会经常使用“解析器”而不是自动机。
众所周知的,LR(0)自动机 A 是 G 的正确解析器,即,$L(A) = L(G)$;但是,由于“非连续”状态的存在,通常它是非终结的。一个状态 q 是非连续的,当且仅当,存在一个$t\in T$ ,有$Next(q, t)$ 被定义,$Reduce(q,t) \neq \empty(读-归约冲突)$,或者$|Reduece(q,t)| > 1(归约-归约冲突)$,或两者都存在。
对于特定的移动顺序,一个速记符号是有用的:
$$
[\alpha |]yz \vdash^*[\alpha | \beta]\ 当且仅当 (Top[\alpha], yz)\vdash^*([Top[\alpha]:\beta],z).
$$
这个描述了一个概念,解析器读到 $y$ ,然后归约它到 $\beta$,可能包含 $y$ 前面的空字符串归约。竖线是必须的,因为$[\alpha]yz \vdash^*[\alpha \beta]z$ 并不一定意味着 $y$ 归约到 $\beta$。例如,考虑到$[\gamma A]txz\vdash_{read}[\gamma At]xz \vdash_{A\rightarrow At} [\gamma A]xz \vdash^*[\gamma A \beta]z$,其中 $tx$ 不会归约到$\beta$(这里$y = tx $和 $\ \alpha = \gamma A$)。
图
一个有向图是一对$(V’, E)$,其中$V’$ 是一组顶点,$E$ 是 $V’ \times V’$ 的子集,它的每个成员叫作边。在本文中,$V’$ 总是有限的。一个有向图路径,或者简化一个路径当上下文是清楚的,是一串顶点$V_1, \cdots,V_n\ ,n > 1$,因此有,$(V_i, V_{i + 1}) \in E, 对于 1 \leq i <n $ 成立;我们说存在一条从 $v_1$ 到$v_n$ 的路径。一个根顶点是一个没有路径到达它的顶点。一个有向无环图(DAG)是一个有向图,其中每个顶点都不存在到它自己的路径。一个森林是一个 DAG,其中每个顶点到给定顶点最多只有一条路径。一颗树一个森林,它只有一个确定的根顶点。
LALR 向前看集
“LALR(1)解析器” 可以通过提炼 LR(0)解析器的归约定义来定义。 直观地,$Reduce(q, t)$ 应该包含 $A \rightarrow \omega$ 只要存在语法 $\alpha A tz$ 和 $\alpha \omega tz$ ,则 $\alpha \omega$ 接收 q。在 “向前看符号”(LA)的定义之后给出 LALR(1)解析器的定义:
定义. 对于一个 LR(0)解析器,
$$
LA(q, A \rightarrow \omega) = { t\in T | [\alpha \omega]tz \vdash_{a \rightarrow \omega}[\alpha A]tz\vdash^*[S’\perp], 则 \alpha\omega 接收 q}.
$$
定义. 一个 CFG G 的 LALR(1)解析器与 G 的 LR(0) 解析器类似,除了
$$
Reduce(q, t) = {A\rightarrow\omega | t \in LA(q, A\rightarrow \omega)}.
$$
定义. 一个 CFG 是 LALR(1),当且仅当它的 LALR(1)解析器没有不一致的状态。
后者根据LALR(1)解析器定义了 LALR(1)语法;一个语法是LALR(1),当且仅当它的LALR(1)解析器是确定的。最好有一个LALR(1)语法的定义不涉及解析器,但我们知道没有合理的方法可以做到这点。然而,我们确实在以下定理中更接近一点了,Watt 给出它作为定义[24]。
$$
定理.LA(q, A\rightarrow \omega) = {t\in T | S \Rightarrow^* \alpha A tz\ 和\ \alpha \omega 接收 q}.
$$
这个证明本质上依赖于LR(0)解析器的正确性,即,移动忠实地反映了推导过程;我们不会在这里证明它。
这里主要的目标是给出了如何计算 LA 集。为此,我们主要关注在非终结符转化,定义它们的“follow sets”。
定义. 对于一个有非终结转化的 $(p, A)$ 的 LR(0)解析器,
$$
Follow(p, A) = {t\in T | [\alpha A]tz \vdash^*[S’\perp] 和\ \alpha 接收 p}.
$$
这些只是可以在句子中跟随 A 的终结符,它前缀$\alpha$,前一个是 A,接受状态 p,给定 LR(0)解析器的正确性。根据推导说明,$Follow(p, A) = { t\in T | S \Rightarrow^* \alpha Atz 和\ \alpha 接受 p}$。因此,可以容易地看到每个 LA 集只是一些相关 FoLLow 集的并集。
定理 并集
$$
LA(q, A\rightarrow \omega) = \cup{Follow(p, A)\ |\ (p, A)是一个转换,p-\cdots^*\rightarrow q}.
$$
(证明在附录中给出。)就是说,处在状态 q 的产生式 $A \rightarrow \omega $ 的 LA 集是 A-转换的并集,它们的源状态 p 有一条路径为$\omega$,其终结在 q 上。直观地,当解析器在状态 q 归约 $\omega$ 到 A,在$\omega $弹出后,每个这样的 p 是一个可能的顶部状态;然后,解析器必须读 p 中的 A,都有一些终结符 t,输入的第一个。
图解,
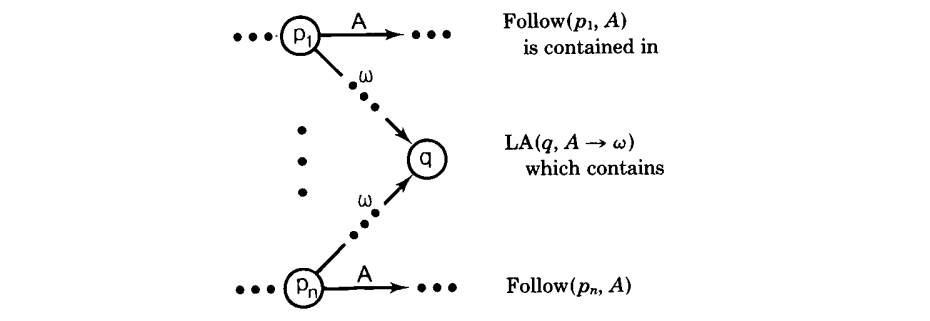
当解析器处在状态 q,如果下一个输入符号 t 是$Follow(p_i, A)(1 \leq i \leq n)$ 中的任意一个时,它需要归约$A\rightarrow \omega $,即,如果 t 可以跟随 A 在任意被状态$p_1$到 $p_n$ “记住”的上下文左侧。关心的转换式$(p_i, A)$可以通过下面的关系获得:
$$
定义[24].(q, A\rightarrow \omega)\ 向后看(p, A)\ 当且仅当 p -\cdots^\omega\rightarrow q.
$$
因此,$LA(q, A\rightarrow\omega) = \cup{Follow(p,A) | (q, A\rightarrow\omega) 向后看(p, A)}$.
反过来,Follow 集是相互关联的。特别是,
定理,$Follw(p’, B) \subseteq Follow(p, A) $ 如果
$$
B \rightarrow \beta A\gamma, \gamma \Rightarrow^* \epsilon, 且 p’ -\cdots^\beta \rightarrow p.
$$
图解,
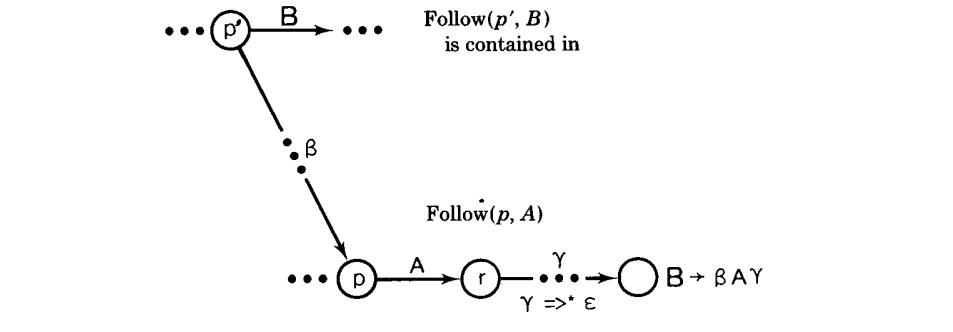
这很容易看到,因为,给定一些字符串 $\alpha$ 接受 $p’$,我们有$\alpha \beta$ 接受 p,在适当的右侧上下文中,$\alpha \beta A$ 可以首先归约到$\alpha \beta A \gamma$,通过$\gamma \Rightarrow^* \epsilon$,则到$\alpha B$。因此,在$p’$记住的左侧上下文可以跟随 B 的那些符号,也可以在 p 记住的左侧上下文中跟随 A。上述的包含可以通过非终结符转换的关系来获得。
定义. $(p, A) 包含(p’, B)$ 当且仅当
$$
B \rightarrow \beta A \gamma,\ \gamma \Rightarrow^* \epsilon, 且 p’-\cdots^{\beta}\rightarrow p.
$$
因此,$Follow(p’, B) \subseteq Follow(p, A)$ 当 $(p, A) 包含(p’, B) $ 时成立。
下一步,观察到标记终结转换“跟随”非终结转换$(p, A)$的符号显然在$Follow(p, a)$。
定理。$Read(p, A) \subseteq Follow(p, A)$。
其中,
定义。对于一个 LR(0) 解析器,带有非终结转化$(p, A)$,
$$
Read(p, A) = {t\in T | \alpha 接受 p 且[\alpha A|]tz \vdash ^* [\alpha A | \gamma ]tz \vdash_{read}[\alpha A \gamma t]z \vdash^*[S’\perp]}.
$$
图解,
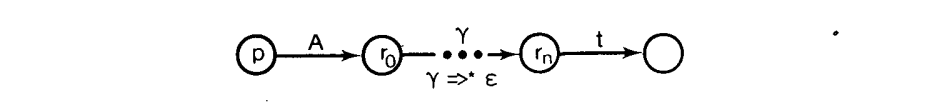
$Read(p, A)$ 是任意包含 A 的短语被归约前可以读取的终结符的集合。由于空字符串的许多归约的可能性和非终结符产生的,定义是复杂的,即,$\gamma \Rightarrow^* \epsilon$,在读移动最后发生之前。$Read(p, A)$ 只是从$r_0$“直接读符号”(DR, 下面表示),如果$\gamma = \epsilon$ 在上图中(即,n = 0)。
已经考虑到所有对 Follow 集的贡献,这个结果被总结到了下面的定理中,其中前两个定理是推论:
向上定理
$$
Follow(p, A) =_s Read(p, A)\cup \bigcup{Follow(p`, B) | (p, A) 包含 (p’, B)}.
$$
(证明在附录中给出。)这就是说,$Follow(p’, A)$ 是确定的(1)可读的终结符集合,通过第一个读,在归约一个短语到左上下文由 p ”记录“ 的A 之后,在任意包含 A 的短语被归约之前,伴随着(2) 非终结的 Follow 集到它的一些包含 A 的短语,后面最多跟随着一些可以为空的非终结符,在读到其它符号前,可以被归约,当然,每个这样的非终结符在合适的左上下文中。图解,对于 n 个这样的终结符,$B_1$ 穿过 $B_n$。
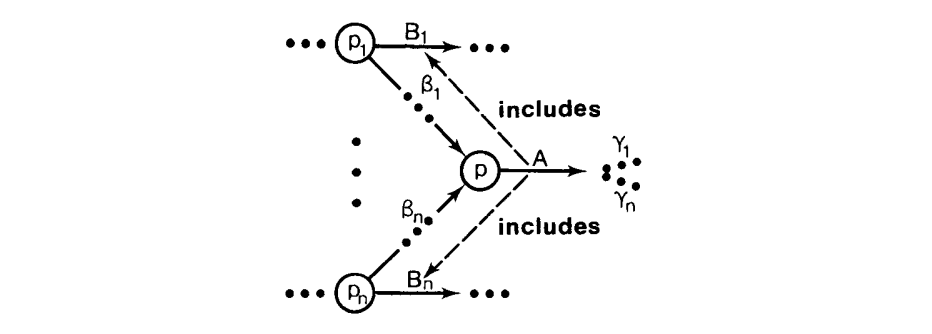
($B_i,B_j;\beta_i ,\beta_j;\gamma_i ,\gamma_j$ 不必要不同。)虚线箭头表示包含关系。在相似的方式下,Read 集可以被分解。
交叉定理
$$
Read(p, A) =_s DR(p, A) \cup \bigcup {Read(r, C) | (p, A) 读取 (r, C)}.
$$
(在附录中给出证明。)
其中,
定义。对于一个有非终结符转换 $(p, A)$ 的 LR(0)解析器,
$$
DR(p, A) = {t \in T | p \longrightarrow^A r \longrightarrow^t}.
$$
定义。$(p, A)$ 读 $(r, C)$ 当且仅当 $p \longrightarrow^A r \longrightarrow^C$ 且$C \Rightarrow^* \epsilon$.
“直接读符号”(DR) 就是那些标记了$(p, A)$转换的后继状态 r 的终结转换。当可以为空的非终结符可以跟随,出现“间接读符号”。图解,

此处,$(p, A)$ 读 $(r_0, C_1)$ 读$\cdots$ 读 $(r_{n - 1}, C_n)$;因此,$DR(r_{n - 1}, C_n) \subseteq Read(p, A)$,且$t\in Read(p, A)$。
总的来说,为了计算 LA 集,需要 Follow 集,然后因此需要 Read 集,然后在因此需要 DR 集。Follow 集是相关的,由 include 关系描述的,Read 集由 Read 关系描述。在下一节中,通过沿着带有 Reads 和 includes 关系的图的边携带信息来描述这些集合的计算。一个图遍历的算法用来决定这样做的最佳顺序,同时计算这些集合。
LALR 计算的图算法
Up 和 Across 定理将 Follow,Read,DR 关联在一起,首先可以应用一个合适的图遍历算法从 DR 计算出 Read,然后从 Read 计算出 Follow。注意到 DR 在 LR(0)解析器中是直接有效的。两个兴趣图分别是包含 Reads 关系和 includes 关系。但是,首先让我们考虑一个更通用的问题,然后在回到这个特定的 LALR 应用。
通用场景
令 R 是 集合 X 中的一个关系。令 F 是一个值集合函数,对于所有的$x\in X $,
$$
F x =_sF’x \cup \bigcup{Fy |xRy} \ \ \ (4.1)
$$
其中,$F’ x$ 给到所有的$x \in X$。令$G = (X, R)$ 是包含 R 的图,即,G 由点集 X 和 $(x, y)$ 是边,当且仅当 $xRy$。然后,通过适当地遍历 G 可以高效地从$F’x $ 中计算出$Fx$,首先,我们考虑 G 是一个森林,然后是一个DAG,最后是一个通用的图。
假设 G 是一个森林,如
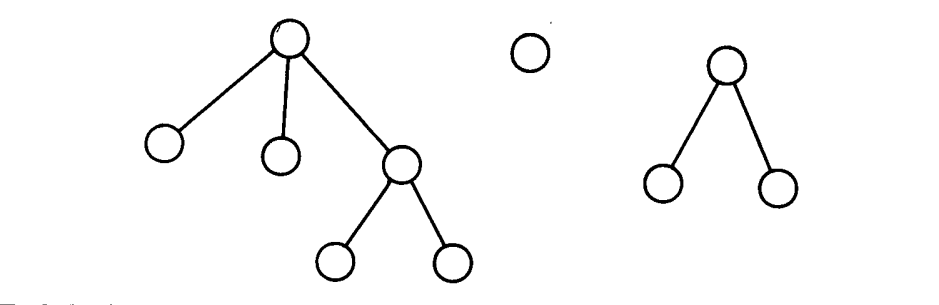
每个叶子 x 不存在 y 使得 $xRy$;因此,$Fx$ 类似于$F’x$。每个非叶子节点是一个或多个子节点的父节点;x 的一个子节点是顶点 y ,有 $xRy$,则在这个场景下,$Fx$ 是 $F’x$ 并上 x 的子节点的 F-值。因此,一个标准的,递归的,树遍历算法 T 可以用于计算这个场景下的 F,通过将信息从叶子传递到根节点。
现在考虑一个 DAG,如
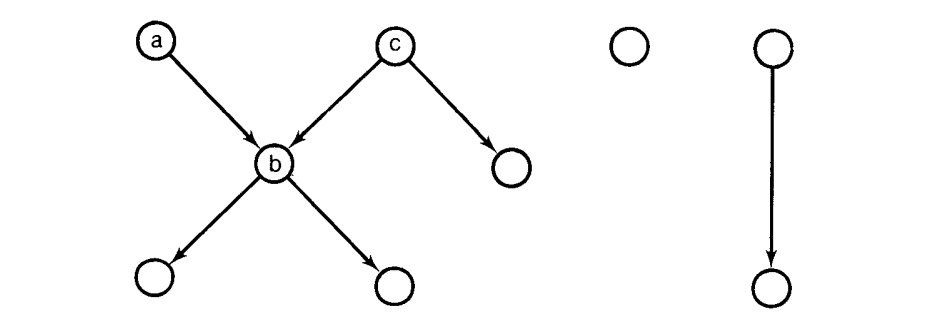
点 a 和 b “共享” 子节点 b。算法 T 为每个节点正确地计算 F,但它遍历 b 和它的子树两次,一次是计算 $Fa$ 的子任务,然后是计算 $Fc$ 的子任务。一个算法 D,基于 T,通过对每个点第一次遇到时进行标记,然后不会重复遍历标记过的顶点,来避免重复计算。
最后,考虑一个带有循环或者可能没有根节点的通用场景,例如,
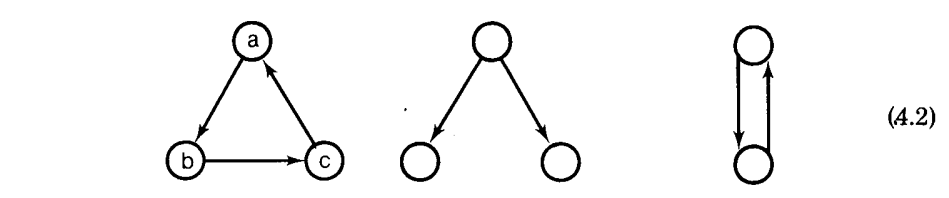
如果算法 D 在节点 a 开始它的遍历,它会访问 a 然后 b 然后 c,不正确地计算$Fc = F’c\ \cup F’ a$ ,虽然它会正确地计算$Fa$ 和$Fb $。更糟糕的是,算法 T 将会死循环。注意,根据 F 的定义,$F a \subseteq Fb \subseteq Fc \subseteq Fa$,所以 $F a = F b = Fc = F’a\ \cup F’b\ \cup\ F’ c$。循环第二遍遍历将会解决上述简单循环的问题,但是在通用场景中,存在循环嵌套循环,或者循环间短路径,因此,“第二次遍历”不容易定义。
这种循环的泛化表示为 强连通分量(SCC),一个图 $G = (V’, E)$的最大顶点子集 $V’’$,对于其中的每个不同的$v_i, v_j \in V’’$,存在一条从 $v_i$ 到 $v_j$ 的通路(因此,反之亦然)。称一个 SCC 是平凡的,当且仅当它是一个单顶点,没有到自己的路径(回想下,有向图路径的长度必须是一或者更长)。这个感念在后面的定理中比较重要。
如上图所示,可以容易的看到,如果 $V’’ = {x_1, \cdots, x_n}$,则 $Fx_1 = \cdots= Fx_n$ 且这个通用值包含$F’x_1 \cup \cdots \cup F’x_n$。因此,每个 SCC 都可以压缩成一个顶点$x’’$, $x’’$ 带有$F’x’’ = F’x_1 \cup \cdots\cup F’x_n$,形成一个新的图$G’$。然后可以在上面应用算法 D,它的结果可以从 G’ 分散到 G,例如,$Fx_1 = \cdots Fx_n = Fx’’$。已知如果所有的 SCC 都塌缩成顶点,则 $G’$ 就没有循环了,即,会变成一个 DAG 的。因此,算法 D 将会在 G’ 上正确运行的。
注意到 G 中的每个顶点 $v$ ,如果没有关联在任意的循环里,将会是一个平凡 SCC 的唯一成员,因此出现在 G’ 不改变的部分里。例如,下图
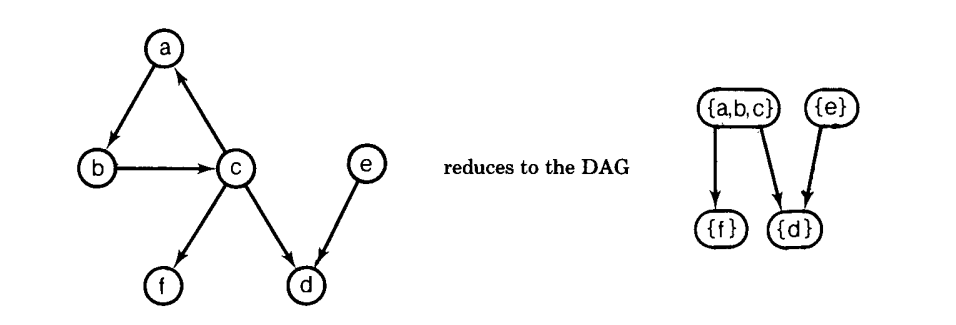
实际中,塌缩成的图 G’ 不需要实际的构建。相反,F 的计算可以在寻找 SCC 的同时进行计算。如下图的算法,是 Eve 和 Kurki-Suonnio 给出的其中一个的自适应[14]。首先我们修改算法的表达来提高它的可读性和可理解性。然后我们从右出发将三个表达式相加来计算 F。更多的解释由下面的算法给出。

数组 N 用于三个目的:(1)记录未标记的顶点($N x = 0$),(2)将正整数值关联到那些正处于活跃考虑中的顶点($0 < N x < Infinity$),(3)标记那些 SCC 已经被找到的 Infinity 顶点。每个未标记的顶点都被标记过了。遍历会将它的参数压到栈 S 上,在 S 上用它的深度标记它(通过 N),然后遍历它的“子树”。如果一条边从一些后继 D 到一个已经在栈上的祖先 A 曾经被遇到过(见下图(4.3)),则存在一条从 A 到 D 在到 A 的路径,因此,至少 A 和 D 以及栈上的中间节点属于一个 SCC。D 的 N-值最小化变为 A 的 N-值,从而防止 D 在递归展开时被弹出。(在图(4.3)也有一条从 A 到 B 的边;因此 A 和 B 都是在同一个 SCC 中。)
最后,当一些节点 B 的所有“子树”已经遍历了,B 的 N-值还没归约,则 B 被识别为一个 SCC 的根节点(在图(4.3)的{B, A, D})。当这个 SCC 的成员被弹出,它们被标记为 Infinity。这防止对其它 SCC 的发现产生干扰,例如,{Y,Z}。如果,对于图(4.3),N A 没有设置为 Infinity,N Z 将会被设置为 2,算法会不正确地声明 {X,Y,Z} 为一个 SCC。
定理。算法图正确地确定了 SCCs。
对于证明,读者可以参考 Eve 和 Kurki-Suonio 给出的[14],因为图只是它们算法的轻微修改。
线性度定理。算法图根据包含关系 R 的图的 $|Vertices| + |Edges|$ 进行排序,即,线性于 R 的“大小”。
证明。遍历是每个顶点走一次,由于立即标记,可以避免重复遍历标记过的顶点。在遍历中,v 被压到栈上一次,对于v 的每条边 for-loop body 只被执行一次。repeat 循环只是间歇性地执行,当 SCC 确定,简单地从栈上弹出顶点;最终$|Vertices|$ 被弹出,因为压栈了许多了。因此,每个顶点被压栈和弹栈一次,每条来自它的边被遍历一次。
推论。算法图执行关系 R的每条边的集合,即,$F x \leftarrow F x \cup Fy$。
事实上,可以归约每个非平凡 SCC 里这种并集的数量,即从边的数量到 SCC 中的顶点的数量[14]。这种提高在带有许多终结符号的语法中的“高连接”的 SCCs 中变得比较重要,即,这种情况下集合并集变得昂贵了。这里我们没有包含提升(也不在我们的实现中[12]),因为它会掩盖基本算法。此外,在实际中,非平凡 SCCs 出现得比较少。
定理。算法图可以正确计算 F。
证明。这个定理基于如下得事实。首先,如果 $Fx$ 满足(4.1),则$Fx = \bigcup{F’y | x R^y}$;这是因为下面的完备性定理产生的。第二,图隐式地计算了$R^[14]$。事实上,如果$F’ x = {x}$,对于所有的$x\in X$ 成立,则$Fx = {y \in X | x R^*y}$,所有的顶点从包含 R 的图中的 x 都是可达的。
完备性定理。假设 F 和 F’ 是 $X \times 2^z$ 上的函数 ,R是$X \times X$ 上的关系 a。如果 $\forall x\in X:Fx =_s F’ x\cup\bigcup{Fy|xRy}$,则$\forall x\in X: Fx=\bigcup{F’y | xR^*y}$。
(证明在附录中给出。)
应用到 LALR
令算法图中的集合 X 是一个 LR(0)非终结转换的集合。首先,令 $F’$是 DR 且 R是可读的。则 F 的结果会变成可读的,即,根据接受定理,计算结果将会是
$$
Read(p, A) = DR(p, A)\cup\bigcup{Read(r, C) | (p, A)\ 读\ (r, C)}.
$$
第二,令 $F’$ 是 Read ,R 是 includes。则结果 F 将会是 Follow,即,根据 Up 定理,
$$
Follow(p, A) = Read(p, A) \cup \bigcup{Follow(p’, B) | (p, A) includes (p’, B)} .
$$
最后,计算
$$
LA(q, A\rightarrow \omega) = \cup{Follow(p, A) | (q, A\rightarrow \omega) lookback(p, A)}
$$
根据 Union 定理。因此,期望的 LALR(1) 向前看集的结果来自图算法和最后一系列的集合并集的两方应用。
从关系的角度,$t\in LA(q, A\rightarrow\omega)$ 当且仅当$(q, A\rightarrow \omega)$ lookback $(p, A)$ include* $(p’, B)$ reads $(r, C)$ directly-reads t,其中,
定义。$(r, C)$ 直接读 t 当且仅当 $t \in DR(r, C)$。
Watt 提出了这个公式,虽然他(错误地)完全忽略了读关系[24]。Watt 提出的用位矩阵表示稀疏的 reads 和 includes 关系会浪费空间和时间;例如,对于一个特定的 Ada 语法[13],每个向量包含了将近 5 百万位(见 6.1 节表 I)。我们有效地提供了一种有效的方法计算$R = reads^\circ directly-reads(Read)$,则$I = includes^ \circ R(Follow)$,最后是$lookback \circ I(LA)$。
需要有向图
最后,我们需要证明算法图的一般性,因为通常由 includes 和 reads 归约的算法图都可以是非-DAGs的。在每种情况下,非平凡SCC 的存在都意味着对于任意的 k,都不是 LR(k)的,并且可能是模糊的或者可能不是模糊的。
includes 关系中的 SCCs
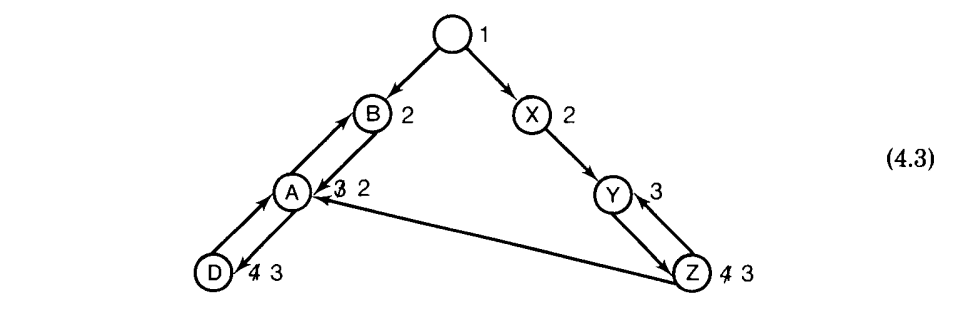
考虑有如下状态图的 LR(0)解析器:
虚线表示有向图的边是由 includes 关系归约的。这个有向图不是一个 DAG,因为它有循环,则对应语法不仅是LALR(1),也是 LR(0)。(添加产生式$A\rightarrow b$ 会让它变成非-LR(0),但依然是 LALR(1)。)
然而,上述的例子是“危险地接近于非-LR”的,在某种意义上讲,如果 Read 集对于循环中关联的 A-,B-,C-转换都不是非空的,则对于任意的 k,语法都不是 LR(k)。我们相信,这个语句的如下一般化是成立的:
Includes-SCC 猜想。令 $(p, A)$ 是一个非终结转换,它在一个有向图的非平凡 SCC 中,由 include 关系归约。然后,如果 $Read(p, A) \neq \empty$,则对于任意的 k ,相关语法不是 LR(k)。
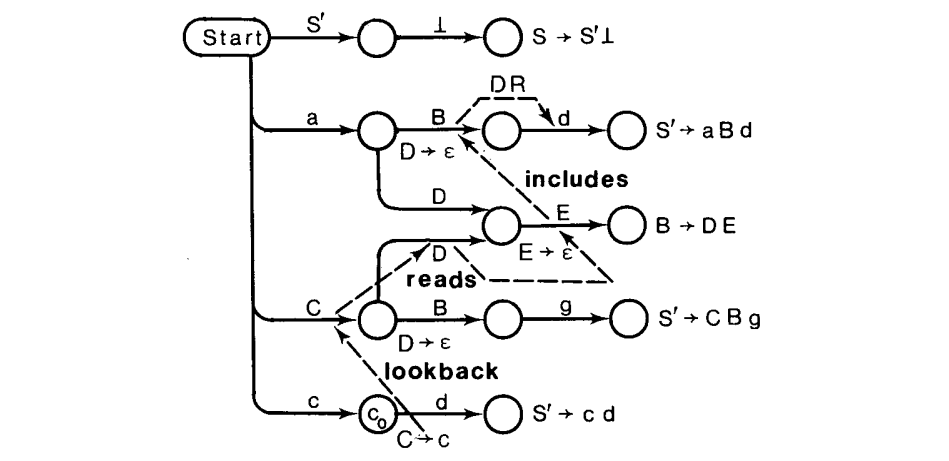
通过添加一个产生式 $B \rightarrow cCf$,这样的问题可以由上述的解析器 说明。状态 $C_0$ 的改变如下:
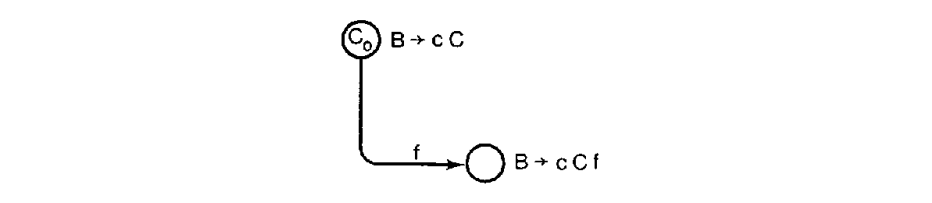
因此,f 在 C-转换的 DR,Read 和 Follow中;然后有它在循环的 A-转换的 Follow 集中;然后有它在B-转换的 Follow 集中;然后有它在$LA(C_0, B \rightarrow cC)$;则因此,这里有读-归约冲突,因此 f 也可以从状态$C_0$ 中获得。(符号 $\perp$ 是每个 Follow 集中的唯一其它符号,是由于 A-转换来自初始状态产生的。)
这个语法不但是非-LR的,也是有歧义的。这个歧义在 $B \Rightarrow^* cdbB$ 和 $B \Rightarrow^cdbBf$ 都是明显的。这本质上是“悬挂 else 问题”,其中 f 是 else 子语句, cdb 是 if-then 子语句:$B \Rightarrow^ cdbB \Rightarrow^cdbcdbBf$,以及明显的 $B \Rightarrow^ cdbBf \Rightarrow^* cdbcdbBf$。
通过添加可以为空非终结符字符串到各种生成式的尾部和在这个被添加的产生式的 f 之前,这个例子可以做成任意微妙和复杂的形式。此外,例如将 $B \rightarrow cC$ 变成 $B \rightarrow cCX$,其中 $X\rightarrow \epsilon$,仍然会在符号 f 上产生一个读-归约冲突,但是现在,在状态$C_0$上涉及的产生式是$X \rightarrow \epsilon$。如果被替换的$ B \rightarrow cCf$ 被改成 $B \rightarrow cCXf$,则在状态 $C_0$ 的符号 f 上会有归约-归约冲突,因为$LA(C_0, B\rightarrow cC) = {f, \perp} 且 LA(C_0, X\rightarrow \epsilon) = {f}$。
reads 关系中的 SCCs
现在考虑有如下状态图的 LR(0) 解析器
此处虚线表示 reads 关系的边。对于 B-转换和 C-转换两个的 DR 都是空的,但 D-转换是${a}$。
因此读每一个都是 ${a}$,因为 B 的 read C-,C- reads D-,以及 D-reads(下降) B-转换。因此,在状态 $D_0$ 的符号 a 有个读-归约冲突,因为,$LA(D_0, B\rightarrow\epsilon)$ 包含下降 B- 的 Follow,其包含下降 B- 的 Read,然后包含 a。
在这个特定的场景中,这个语法是由歧义的,因为空字符串在归约到 A 之前可以被归约到 BCD 许多次,在这个语言中唯一的 a 在唯一的字符串中。但是,通过改变产生式 $A\rightarrow BCDA$ 到$A\rightarrow BCDAf$ ,可以消除这个歧义,但保留这个冲突。现在这个语法是无歧义的,因为 f’s 的数量固定了空到 BCD 的产生式的数量,但是对于任意的 k 它仍然不是 LR(k),因为,在 a 被归约到 A之前,BCDs 必须被归约,但是通常 f‘s 跟随着 a。
READs-SCC定理。如果有向图被包含 a 非平凡 SCC 的 reads 关系归约,则对于任意的 k,相关的语法不是 LR(k)。
过度简化
两个“清楚的主意”浮现在脑海中,下面显示的每一个都是不充分的。
NQLALR(1) 解析器
最值得注意的一个是,LALR(1)向前看集的计算的过度简化,已经被一些研究者独立发明了[7, 11, 23, 25],并且持续地被重新发明。它涉及到定义另一个 receives 关系,它紧密地关联于 includes 和 reads 的并集,从而有了我们称为”不全是 LALR(1)”或者 NQLALR(1)解析器。这个基础的想法是关联状态的,而不是转换。这个的原因是 $LA(q, A\rightarrow \omega)$ 必须包含所有的可以被向前看 或者从任意“重启”状态 s 读到的符号,比如,有个“向后看”状态 r ,带有到 s 的 A-转换,以及称为 $\omega$ 到 q 的路径:
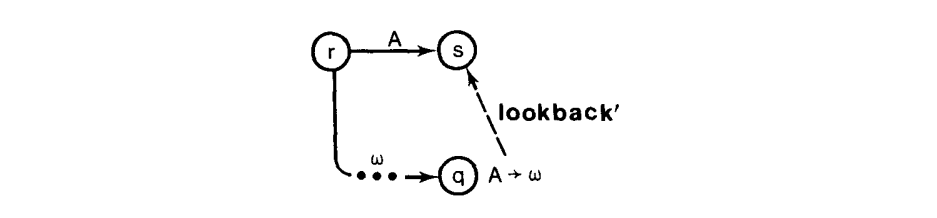
如果在 q 时 $\omega$ 被归约到 A,在弹出 $|\omega|$ 状态之后,r 可能会成为顶部状态。然后读到 A 且 s 进入,因此,任意向前看或者由 s 读的符号都会在 $LA(q, A\rightarrow\omega)$,或者在 $NQLA(q, A\rightarrow \omega)$。任意从 s 通过归约可达的状态 s‘ 也由贡献:
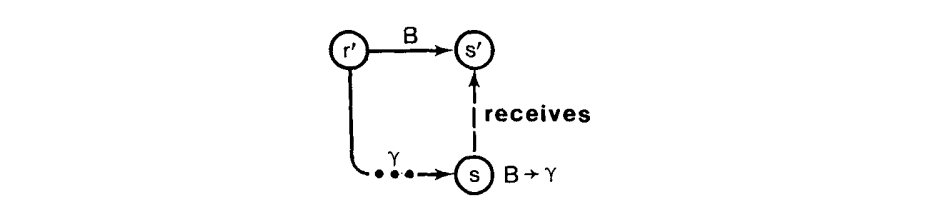
如果我们在 s 上归约 $\gamma$ 到 B,则我们可能会进入状态 s’,任意对 s’ 有效的符号时$NQLA(q, A\rightarrow\omega)$。形式化,
定义。$(q, A\rightarrow \omega)$ lookback‘s 当且仅当有一个$r \in K$ 则
$$
r \longrightarrow ^A 和 r\ -\cdots^\omega\rightarrow q,其中 A\rightarrow\omega\cdot\in q.
$$
定义。s receives s’ 当且仅当 $(s, p)$ lookback‘ s’ 当且仅当一些产生式 p。
定义。
$$
NQLA(q, A\rightarrow \omega) = \bigcup{NQFollow(s) | (q, A\rightarrow \omega) lookback’s}.
$$
定义
$$
NQFollow(s) =_s NQDR(s) \cup \bigcup{NQFollow(s’) | s receives s’}.
$$
定义。$NQDR(s) = {t \in T |Next(s, t) 被定义}$,即,除了为状态而不是转换定义,都与 DR 相同。
定理。$NQFollow(s) = \bigcup{NQDR(s’) | s receives^*s’}$.
引理
$$
NQLA(q, A\rightarrow \omega) = \cup{NQDR(s) | (q, A\rightarrow\omega) lookback’s \circ receives^* s}.
$$
这个定理来自于将等价定理应用到 NQFollow 的定义里,而引理来自于后向替代进入 NQLA 的定义里。
注意到此处可以为空的非终结不会导致问题。例如,
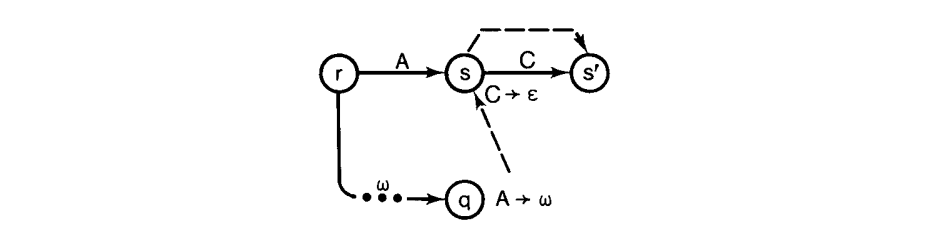
从 s 到 s’ 的虚线箭头直接来自于 receives ,显然其目的类似于 reads 的边。因此,$NQLA(q, A\rightarrow\omega)$ 只是所有通过$lookback’\circ receives^*$ 可达的状态的 NQDRs的并集。我们老的 IBM 360 实现 [11] 只是通过位矩阵技术计算$lookback’\circ receives ^*$ ,然后合并相关的 read 集(NQDR)来获得 NQLAs。
NQLALR 的不足来自于不当的“归约路径”会被解析器追踪的事实,有效的,第一次归约 $\omega$ 到 A,进入到状态 s,然后在 s 上归约,有$B \rightarrow xA$,当通过归约离开时,不需要涉及导致状态 s 的相同 A-转换。
下面的 LR(0)解析器说明了这一点:
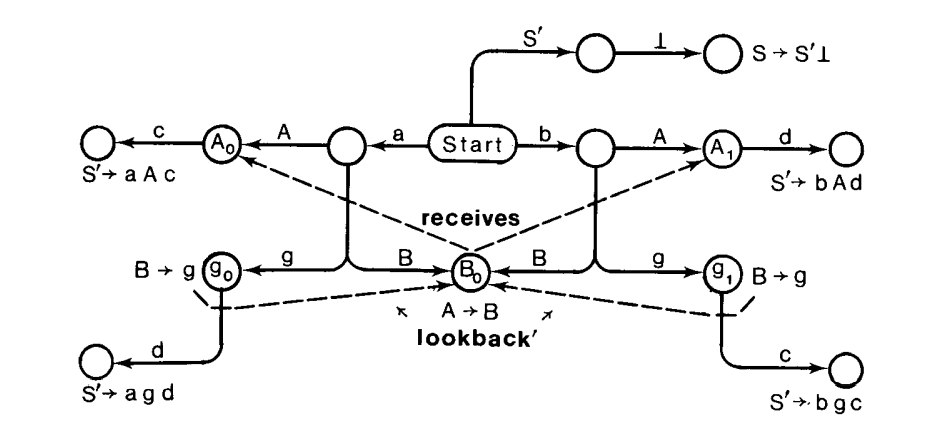
相关的 receives 和 lookback 的边通过虚线箭头表示。
在这个场景中$NQLA(g_0, B\rightarrow g)$ 和$NQLA(g_1, B\rightarrow g)$ 都包含${c, d}$,因为 receives 关系将状态 $B_0$ 和状态 $A_0$ 与 $A_1$ 连接,其可以重复地读 c 和 d。然而这个语法不是$NQLALR(1)$,因为我们在状态 $g_0$ 和 $g_1$ 中有读归约冲突。但是,这个语法是 LALR(1)的,我们正确的方法(和新的实现[1])产生了$LA(g_0, B\rightarrow g) = {c}$ 和$LA(g_1, B\rightarrow g) = {d}$,这些是正确的 $LALR(1)$ 集。这对于读者绘制两个 lookback 边和 两个 include 边和观察解析器两半是如何保持分离的具有指导意义。
容易看到 $LA(q, A\rightarrow\omega) \subseteq NQLA(q, A\rightarrow\omega)$ ;因为 $(q, A\rightarrow \omega)$ lookback(p, A) 当 $(g, A\rightarrow \omega)$ lookback‘$Next(p, A)$,而$(p, A)$ includes$(p’, B)$ 当 p receives $Next(p’, B)$。NQLALR 向前看集只是”轻微大于”LALR向前看集。实际上,我们已经遇到的只有很少的编程语言语法是 LALR 却不是 NQLALR 的。但是 NQLALR 是基于 SLR 的巨大提升。总之,$SLR-LA(q, A\rightarrow \omega) \supseteq NQLA(q, A\rightarrow \omega) \supseteq LA(q,A \rightarrow \omega)$.
合并 includes 和 reads
第二阶段简化由合并 includes 和 reads 组成,只运行一次有向图算法。这意味着不是计算上面描述的式子
$$
Follow(p, A) = \bigcup{DR(r, C) | (p, A) includes^\circ reads^(r, C)}
$$
(这个公式可以通过应用完备定理到重写 Follow 和 Read 表达式(见Up 和Access定理),以及在重写的 Follow 中后向替代重写了的 Read,获得),而是计算
$$
Follow(p, A) = \bigcup{DR(r, c) | (p, A)(includes \cup reads) * (r, C)}.
$$
通常这两个方程式不是等价的,如下反例可以说明这种情况:
$LA(c_0, C\rightarrow c)$ 包含 c-转换的 Follow,其读取 D-,读取 E-,includes B-转换的上界,这些的 DR 包含 d,因此,一个读-归约冲突产生了$c_0$。另一方面,通过正确的方法,LA 集只包含 g。 我们看到没有人过度简化,但当我们尝试归约有向图的应用的数量,从两个到一个的时候,它在我们这发生了。
LALR 实现
一个完整的从 LR(0)自动状态机计算 LALR(1)向前看集的过程如下:
A. 计算出那些可以为空的非终结符。
B. 为 DR 初始化读:每个非终结符的转换的一个集合(长度的位向量终结符数量),通过转换的后继状态的检查。
C. 计算 reads:每个非终结转换的一列非终结转换,通过最后转换的后继状态的检查。
D. 应用有向图算法到 reads 上来计算 Read;如果识别到环,说明对于任意的 k 语法不是非 LR(k)的。
E. 计算 includes 和 lookback:重复地,每个非终结转换和归约的一列非终结转换,通过每个非终结转换的检查和相关的产生式的右侧,以及通过适当地考虑可为空非终结。
F. 应用有向图算法到 includes 来计算 Follow:使用与 B 中初始化并在 D 中完成的相同集合,即作为初始值用作为工作区间。如果一个循环在 Read 集不为空的情况下识别到,则说明(如我们推测的)对于任意的 k 这个语法不是 LR(k)的。
G. 根据 F 中计算的 lookback 链合并 Follow 集来形式化 LA 集。
H. 检查冲突;如果没有,则说明这个语法是 LALR (1) – 我们有个解析器。
效率
需要的位向量数量和遍历的关系边数量可能可以通过下面给出的策略最小化。
首先,如果 $ x\neq Top\ of\ S $,则有向图算法中的赋值 $F(Top\ of\ S) \leftarrow F x$ 应该已经完成了。这个节省了平凡(单独的)的 SCCs 的集合拷贝开销,这实际上是占大多数的。避免所有的非平凡 SCCs 中的集合拷贝开销,可以通过引用赋值,即,有 F (S 的 Top)和$Fx\ point$ 到相同的位向量,将不能工作;这里描述的方案使用相同的位向量来表示每个非终结转换的 Read 集和 Follow 集。因为 reads 和 includes 关系的 SCCs 是不同的,这个暗示着不同的“共享”以及实际上会使算法无效。)
下一步计算上面步骤 E 里描述的 includes 和 lookback 关系。初始化,不给非终结转换分配集合。如果语法包含任意的可为空非终结符,然后仅对 reads 关系中涉及的每个非终结符转换,应用有向图(有 R = reads)来计算$Read(p, A)$。之后,只有有集合分配的转换会成为那些在 reads 关系中涉及的(通常地,很少或者根本没有)。对于每个这样的转换$(p, A)$,集合会等价于 Read(p, A)。
比起特殊识别 reads 关系中涉及的转换,有向图后面的应用可以通过将它用到所有的非终结符转换来达成,这里有向图有如下的修改:删除赋值$F x \leftarrow F’ x$;插入代码来识别预取$(F,x)$或者存储$(F x \leftarrow \cdots)$,$Read(p, A)$ 当 $(p, A)$ 没有集合分配给它。在这样的场景中,有向图应该分配一个集合给$(p, A)$ ,然后用$DR(p, A)(F’x)$ 初始化它。
最后,值得注意的是 reads 关系不需要预计算(上面步骤 C),因为当有向图需要它的时候,它可以简单的从 LR(0)状态机中检索到。
对于每个不一致的状态 q 和 q 中最后的子项$A\rightarrow\omega \cdot$, 沿着每条 lookback 边到非终结符转换$(p, A)$。在$(p, A)$(带有 R = includes) 调用有向图来计算$Follow(p, A)$。使用 lookback 标识的 Follow 集的并集来获得$LA(q, A\rightarrow\omega)$。通过对有向图做出修改,和上面描述计算的 Read 集,任意被有向图检查的转换$(p, A)$,有当计算 Follow 时要么有个分配给它的集合带有Read(p, A),或者有向图将会分配一个集合给它,并初始化它到$DR(p, A)$,其等于$Read(p, A)$,因为没有被分配的集合。因此,$Read(p, A)$ 或者已经被计算了,或者在有向图需要时进行计算。
由于这个策略,集合只在那些 reads 关系中涉及的转换需要,或者在不一致的状态的最后一项的向前看集的计算式中需要;此外每个这样的项需要一个集合来重复它的向前看集。唯一的关系边遍历将会是 reads 边,且 includes 和 lookback 边的子集为向前看集计算所需要。因此,如表 I 所示,只需要更少的集合存储和更少的集合合并。
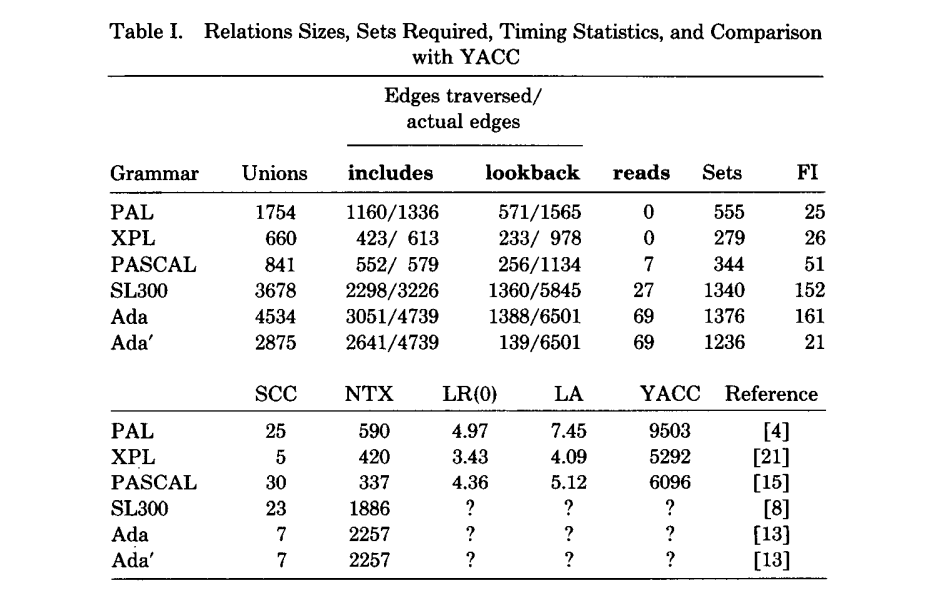
表 I 列出了我们的实现的合并执行的总数。这等于 includes ,lookback,和 reads 边的数量加上反生在有向图拷贝一个 SCC 根节点的 F 值到 SCC 中其它节点的值的少量合并(对于 Pascal,例如,有 4 个 SCCs 带有共 30 个节点,则 841 = 552 + 256 + 7 + (30 - 4))。在处理表中的集合之下,记录了需要的位向量的总数(Read,Follow,LA)。通过减去来自集合行的不一致状态中的最后项(FI)的实际向前看集的数量,可以决定位非终结转换单独分配多少集合。SCC 行记录了非平凡 SCCs 中涉及的 includes 关系的节点的总数量。NTX 是非终结转换的数量。LR(0)计算和向前看(LA)计算的 CPU 时间(以秒为单位)适用于具有 $1.5\mu s$ 的内存和包含LALR(1)条件检查的 HP-3000 计算机。YACC 执行的集合合并通常是我们算法的 5 到 8 倍(YACC 行)。
在 YACC 上运行 SL300 和 Ada 都太大了。它们都不能在内存受限的 HP 3000 上执行,它们能运行的机器上的时间统计信息是无效的。Ada 语法引用接近于处理这个信息的语法;后者还没有发布出来。Ada 的项目在后面的章节解释。
通过只遍历必要的 reads 边,可以有轻微的时间提升。不要分离的适用有向图来计算 Read 集。只能计算 Follow 集。当计算 Follow 集,如果有向图发现一个转换 $(p, A)$ 的 $Read(p, A)$ 还没有计算出来,则它自调用来计算$Read(p, A)$。为了做这个需要分离 $Read(p, A)$ 和 $Follow(p, A)$ 的分配;否则,Follow 和它的 Read 的计算混合将于 5.2 节描述的过度简化相同。因为,reads 边很少,需要的额外空间不值得节省时间。
为了降低存储的开销,一种实现是只存储向前看计算需要的那些 lookback 边。从一致状态的最后项开始的 lookback 边会被丢弃。例如,对于 Ada,只需要 1388 个 lookback 边,总数的 21%。事实上,通过使用 SLR(1)向前看集来解决尽可能多的状态中的不一致,能够节省更多的空间和时间。表中的 Ada 定律表明了有这样做了之后的结果;只有 21 个最后项需要 LALR(1)向前看集,且只有 139 个 lookback 边是有用的。此外,更少 includes 边被遍历到,减少了需要的集合并集和集合的数量。当然,如果一个语法是 SLR(1),则不需要任何的 includes / lookback 计算。
通过应用有向图,SLR(1)向前看集可能可以从 LR(0)解析器和 Read 集中计算出来。SLR-LA$(q, A\rightarrow\omega)$ = SLR-Follow(A) = $\bigcup{Read(p, B) | B \Rightarrow^* \beta A\gamma, \gamma \Rightarrow^* \epsilon, \beta \in V^*, 且(p, B) 是一个非终结转换}$。这个首先是 DeRemer[10] 观察到的,有一些关于可为空非终结符的小错误。换句话说,SLR-Follow(A) = $F’ A \cup \bigcup{SLR-Follow(B) | ARB}$,其中$F’A = {Read(p, A) | (p, A) 是非终结转换}$ 且 A R B,当且仅当$B \Rightarrow^* \beta A \gamma, \gamma \Rightarrow^* \epsilon$,因此,将 SLR 定义转换为一种适合有向图计算的形式。
事实上,Digraph 通常能用于计算上下文无关语法中的其它功能,例如,一个非终结符时候可以从开始符号派生,或者,一个非终结符是否同时是左递归和有递归的。这本质上是因为 Digraph 的关系带有传递闭包的问题[14]。通过一个 Digraph 的变种替换标准快速位矩阵技术,在 MetaWare 的翻译书写系统的语法检查上有三倍的速度提升[12]。对于稀疏关系,Digraph 在计算传递闭包的工作上比位-矩阵技术做的更好。
线性度
Digraph 与它应用到的关系的数量是线性关系,这是由第 4 节的线性定理得到的。对于特定的语法,在一个解析器中,includes 关系的大小(边的数量)大约是非终结转换数量的两到三倍。对于以非终结符 B 结尾的 A ,每个非终结转换 $(p, A)$ 都有一条 includes 边到它的每个产生式,或者 $B \gamma$ 其中$\gamma \Rightarrow^* \epsilon$,即,通常有两个或者三个。reads 关系在实际场景中几乎不存在,所以它可以被忽略。因此,对于实际的 LR(0)解析器,Digraph 几乎是线性于非终结转换的。这些论点都被表 I 给出的统计数据证实。
在最坏情况下,includes 关系的大小与非终结转换的数量的平方是成正比的,因为关系几乎是完全的,即,对于所有的非终结转换 x 和 y,有 x includes y。这种最坏场景由产生式是 ${ S\rightarrow S_1 \perp, S_i \rightarrow S_j , S_i \rightarrow t | 1 \leq i, j \leq n}$。忽略路径$[S_1 \perp]$,这个语法的 LR(0)解析器有 n 个非终结转换,对于任意一个 $S_i$,$1 \leq i \leq n$,有 n 条边到达它;即,每个非终结转换到任意一个其它节点和它自己都有一条边!当然,从实际的观点来看,这个例子是造作的,高度歧义的,没有太大的参考价值。
与其它算法对比
Aho 和 Ulman [3] 的算法和Anderson等的算法[6],通过在隐式(虚拟)图中”传播“向前看集进行运行。当传播造成一个顶点上的向前看信息增加时,这个顶点会进入队列,然后反过来给其它顶点传播新的信息。迭代这个过程直到队列为空。传播的顺序可能不是最佳的,因为每条边只会遍历一次。这导致了 YACC 算法执行性能比我们差得多了,就如表 I 表明的那样。(事实上,YACC 都没有使用队列,而是重复扫描所有的顶点直到传播停止了[3]。YACC 的作者认为这样做,它能在那些它可以接受的摸棱两可的语法上表现得更好,但是事实上比在无歧义的语法上的执行效果更差。)
LaLonde 的算法[20] 本质上是第 4 节的算法 D,但是避免了不正确的向前看集的计算(见图 4.2),对于每个清晰的归约的向前看集的计算中的顶点是不保留信息的。因此,不同向前看集计算的时候,需要重复的遍历边。
与上述算法相反的,我们仅会遍历每条边一次。
Kristensen 和 Madsen [19] 改进了 LaLonde 的算法,完全类似于我们 Follow 集的中间结果被保留,然后用于后续的计算。为了完成这个,Kristensen 和 Madsen 的算法通过偶尔将某些顶点添加到正在计算的集合 $F x$ 中来识别 SCCs。在遍历顶点 x 的后继之后,要么 $Fx$ 不包含顶点,要么它只包含一个顶点 v。在前一个场景中,x 是平凡 SCC 的根节点;在后一个场景中,如果 $v = x$,则 x 是非平凡 SCC 的根节点,集合 $Fy$ 中的 x 的所有事件都被 $F x - {x}$ 替换。这个技术很巧妙,除了莫些地方有点笨拙(这里没有给出全部的细节),然后实际上需要并查集算法[2] 来保证 Kristensen 和 Madsen 算法复杂度(非常接近,但不是精确的)线性于被遍历关系的大小。我们确信他们的算法比我们的产生更大的开销。
Kristensen 和 Madsen 高效地使用了 item-includes 和 item-lookback 关系,这些类似于 includes 和 lookback,但是它们是定义在 items 而不是非终结转换上。因此,遍历的图的顶点是项。因为,解析器中的每个非终结转换 $(p, A)$ 通常是 p 中一个或多个项 $B \rightarrow\delta\cdot A \gamma$ 的结果,Kristensen 和 Madsen 的方法产生了额外的 F 集的开销。因为 Kristensen 和 Madsen 没有给出经验数据,因此然以确定他们算法的实用性。
与之相反的,我们的算法没有使用到 item 概念的地方;因此,所有的 LR 项在向前看集被被计算前都可能会被抛弃。作为结果,我们的算法可能适用于 LR 自动机以外的其它场景中。例如,它可能会定义一个使用优先级技术的自动机,如果应用了我们的算法,它将会计算一些“优先级向前看集”,因此可以确定语法是否是简单优先级的。我们将这些想法留给未来的研究中。
但是,LR 项是必须的,从而能产生下一节描述的诊断调试跟踪信息。
非LALR(1)语法的调试
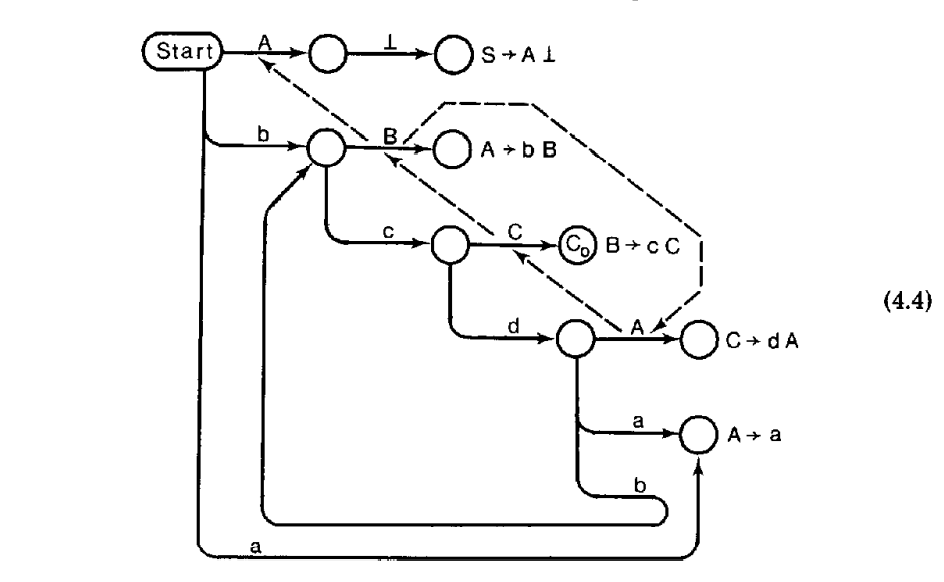
作为我们在向前看集计算领域研究有意思的副产品,我们发现 includes 和 lookback 关系正是为非 LALR(1)语法生成有用的调试信息所需要的。这些边穿过自动机链接回来,从向前看集到冲突符号的源(CSs),特别是那些涉及到冲突的。这正是追踪语法的方式,用户通常是手动查找的。例如,MetaWare 的翻译写系统[12] 为一个解析器处在状态$C_0$ 上的冲突打印大致的跟随流程,如图(4.4),表明加入的产生式$B \rightarrow cCf$ 引入了冲突:
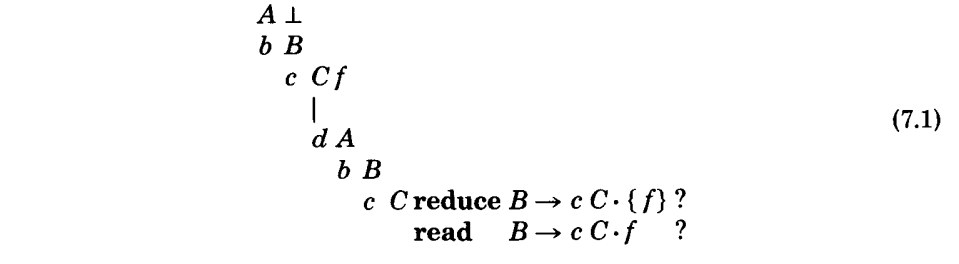
这个图表明在解析器已经读取了 $bcdbcC$ ,然后看到一个 f 之后,有两个行动方案:
(1) 归约 cC 到 B,归约 bB 到 A,归约 dA 到 C,读取 f;或者
(2)读取 f。
在 Top[bcC] 状态上的项 $B \rightarrow cC\cdot f$ 贡献一个 f 给 $LA(C_0, B\rightarrow cC)$,其中利用了产生式$C\rightarrow dA$,$A\rightarrow bB$,以及$B\rightarrow cC$,跟踪一条从$p’ = Top[bc]$ 到$C_0$ 的路径。这个跟踪有两个推导组成,推导的每个右侧部分都垂直位于导出它的非终结符的下面。上面的推导中由单个垂直线组成的行表名开始状态如何跟踪一条到 $p’$ 的路径的。垂直线正上方的式一个项,它给出了向前看符号 f。在垂直线下方的是一个推导,从(非终结符 C 在的)处理中的项到不一致状态,以一个带有冲突的最终项结束。后面的推导包含 lookback 和 includes 边,从陈述$(C_0, B\rightarrow cC$ 到转换 $(p’, C)$,它们的读集包含了 f。$C_0$ 中的项$B\rightarrow cC \cdot f$ 也是使得 f 成为可读符号的原因;因此有冲突。
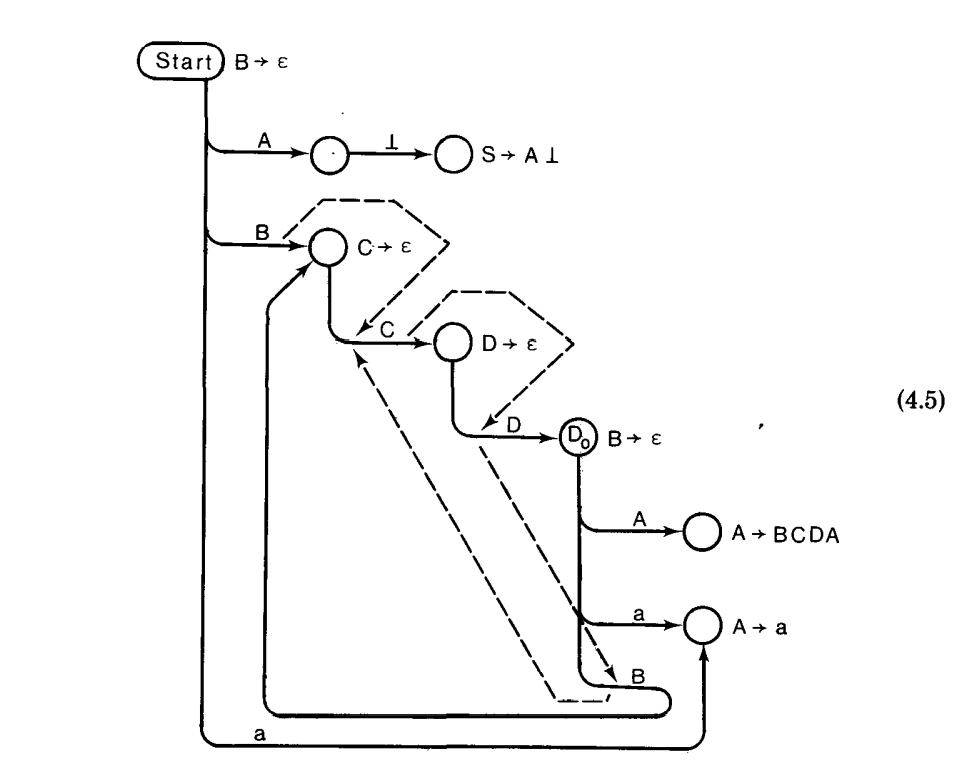
考虑图(4.5)的下一个解析器和状态 $D_0$ 的后续跟踪:

这个解析器两个可选的动作是:
(1)归约 $\epsilon$ 到 C,归约 $\epsilon$ 到 D,读取 a(在 a 被归约到 A 之后);或者
(2)读 a。
在状态$Top[B]$ 的$ A\rightarrow B\cdot CDA$ 项贡献了 a 给 $LA(Start, B \rightarrow \epsilon)$,这是利用了产生式 $B\rightarrow \epsilon$ 的属性和$CDA\Rightarrow^+ A$。后一个推导出现在垂直线“塔”的右侧。关注推导中的 C 和 D 是如何消失的,因为它们可以为空;这里$C\rightarrow \epsilon$ 和$D\rightarrow \epsilon$ 是产生式。要是 C 或者 D 不能直接导出$\epsilon$,额外的推导步骤也可以打印出来;但是,我们觉得这会使得跟踪变得混乱的。
轨迹的通常格式如下:

此处,$Top[\delta_1\cdots\delta_n \alpha B]$中$B_n \rightarrow \alpha B \cdot\beta_1$ 项给$A_{s-1} \rightarrow \alpha_s \cdot$ 的向前看集贡献了 t,因为如图所示的$\beta_1 \Rightarrow \beta_2 \Rightarrow\cdots\Rightarrow t\beta_m$,以及垂直线下面的 产生式链导致了$A_{s-1} \rightarrow\alpha_s\cdot$ 通过$lookback \circ include^*$ 关联到了 B-转换上;这里每个$\gamma_i \Rightarrow^* \epsilon$(但不一定对每个$v_i$都如此)。每个$A_i$ 和$B_i$ 以及 B 产生了它下面的右侧部分。
轨迹的构造是以非一致状态 q 中的一个最后项 $A_{s-1} \rightarrow\alpha_s \cdot$ 为起点,遍历一个 lookback,然后是一些 includes 边直到一个非终结符转换$(p’, B)$ 被找到,它的 Read 集包含 CSs 中的一个。在$Next(p’, B)$ 中存在一个或多个项$B_n \rightarrow \alpha B \cdot \beta_1$ ,有$\beta_1 \Rightarrow^* t\beta_m$ 和 t 是一个 CS。为每一项都打印轨迹(禁止冗余的轨迹;如下)。(值得注意的是,在从 $A_{s-1} \rightarrow \alpha_s \cdot $ 遍历的期间,我们不会检查 Follow 集。虽然 Follow$(p’, B)$ 可能包含 CS,但不保证Next$(p’, B)$ 包含CS-贡献项;Follow$(p’, B)$ 可以从其它的 Follow 集中继承 CS。CSs “起源”于 Read 集,而不是 Follow 集。)
轨迹由三部分组成:
(a)来自 S‘ 的推导,产生了 Next(p’, B) 中的$B_n \rightarrow \alpha B \cdot \beta_1$;
(b)来自$\beta_1$ 的推导$t\beta_m$;以及
(c)一个归约从$(q, A_{s-1} \rightarrow\alpha_s)$ 到 $(p’, B)$ 的includes 和 lookback 边的产生式。
第(c)部分需要在 includes 边的原始遍历上,应用一个宽度优先搜索算法。这使得 includes “链”的大小最小化,对读者给出了“最简单的”可能的解释。归约一条从$(p_1, X_1)$ 到$(p_2, X_2)$ 边的产生式,能被下面的自动机转换重新发现,这个自动机转换来自于 $X_2$ 产生式的右侧下面的状态 $p_2$ 。因此,在 includes 边已经计算之后,归约产生式不在需要冗余存储。
对于(b)部分,计算集合
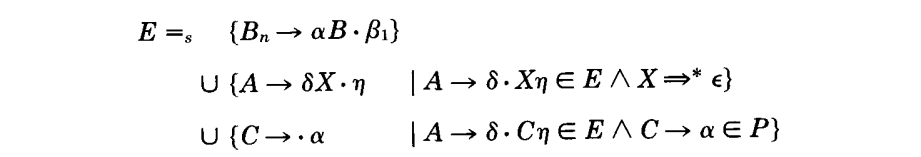
链接 E 添加的回到产生它们的项。带有 t 的$C \rightarrow \cdot t\beta_m$ 形式的项,一个 CS 将会在 E中,然后可以通过下面的链接跟踪回$B_n \rightarrow\alpha B\cdot\beta_1$。然后所有来自 $\beta_1$ 的 CSs 的推导可以产生出来了。
(a)部分需要两个计算。首先找到从开始状态到$Next(p’, B)$的最短路$[\xi]$。在我们的实现中,这意味着重复要求编号最小的状态,其有个到给定状态的转换,因为状态被计算和以宽度优先的方式编号。然后计算
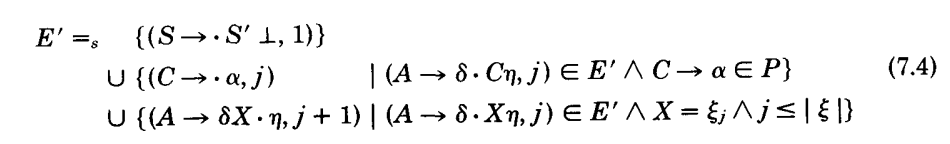
以宽度优先的方式进行,链接到 E’ 的添加回生成它们的组合对中。最终$(B_n \rightarrow \alpha B \cdot\beta_1, |\xi| + 1)$将会出现在 E’ 中,然后计算会停止:所有的 E’ 都不需要计算。期望的产生式序列可能会从链接的检查中获得。宽度优先和$[\xi]$ 是最短路的事实使得产生式序列的大小保持最小。$[\xi]$ 也用于限制 E’ 的大小,通过限制对的添加。
在实际的语法中,一个$B_n\rightarrow \alpha B\cdot\beta_1$ 将会出现在几个不同的左文法中,在每个中都会贡献第一个$\beta_1$ 到相同的特定 LA 集中。因此,为了阻止冗余的轨迹输出,对于 LA 集,每个贡献项都只打印一个轨迹。此外,如果(指轨迹(7.3))$\beta_{m-1}$ 立即推导出超过一个带有 t a CS 的$t\beta_m$ 形式的字符串时,则所有的这些字符串都列在后继行上。
下面是总结了前面的非正式轨迹打印的算法:

读-项 轨迹 。 虽然迄今为止的轨迹方法表明了终结符如何进入向前看集的,它们没有给出(冲突的)读-转换如何出现在不一致的状态中的。对于想要尝试确定为什么解析器在特定的不一致状态下可以归约或者读取的用户,这些信息是有用的。
轨迹(7.3)表明为什么解析器在栈包含$\xi = \delta_1\cdots\delta_n \alpha\alpha_1\cdots\alpha_s$ 时可以归约。轨迹(7.3)相关的读轨迹应该表明,在栈包含$\xi$时,解析器可以读取的原因。这样的轨迹以如下方式出现:
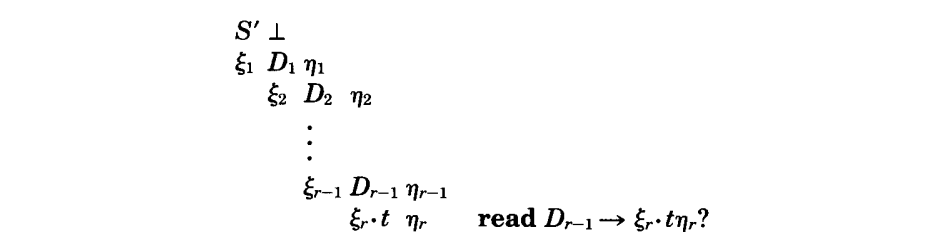
其中$\xi_1 \cdots\xi_r = \xi$ ,每个$D_i$ 产生下一行的右侧部分。$\xi_i$ 上的约束保证了一致性;所以不一致的状态 q 包含了$D_{r-1} \rightarrow \xi_r \cdot t\eta_r$,“冲突”的项。
对于 q 中每个冲突的读项$I = D_{r-1} \rightarrow\xi \cdot t\eta_r$,通过上面的(7.4)描述的计算,可以为 I 构建最短的可能轨迹,除了$\xi$ 被替换为$\delta_1\cdots\delta_n \alpha\alpha_1\cdots\alpha_s$,且当 I 是 E’ 产生的时,计算停止。
对于轨迹(7.1),MetaWare 翻译写系统产生了如下的读-冲突轨迹:
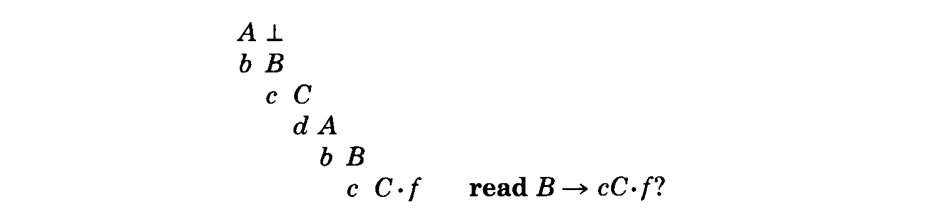
对于轨迹(7.2),相对应的轨迹产生

上面的轨迹太简单了以至于读者可能无法相信它们是很有用的。但是,考虑如下由 MetaWare 翻译写系统为 Ada 语法生成的轨迹,这个语法不是 LALR(1)的:

此处,在左侧上下文 Subprogram-spec is 之后,要么另一个 Subprogram-spec 可以产生一个带有空参数列表的程序头,或者一个 Subprogram-dcln 可以产生一个通用的过程实例。很明显,轨迹可以查明这个问题。
归约-归约冲突和 LALR 与 LR 比较。对于读-归约冲突,我们主张打印相关的轨迹,能显示出读或者归约是合法的,给定一个特定的左上下文(解析栈)$\xi归约轨迹\xi = \delta_1\cdots\delta_n\alpha\alpha_1\cdots\alpha_s)$。 但是在产生式 $p_1$ 和 $p_2$ 之间的归约-归约冲突,我们的算法不需要为了$p_1$ 和 $p_2$ 打印相关的轨迹,即,共用相同左上下文的轨迹。实际上,$p_1$ 可能不存在与 $p_2$ 任意轨迹具有相同左上下文的轨迹。
这里可以发生如下两种情况:(1)这个语法是LR(1),但不是LALR(1);(2)我们的算法出现一个“意外”。在任意一种情况下,调试语法的人都会产生困惑:因为轨迹没有显示出,为什么两个不同的归约移动可能给出一个单一的左语法,他可能无法理解为什么冲突会存在。hua
在第一个场景中,当一个归约-归约冲突同时存在于 LALR(1)和LR(1)自动机中,每个归约(在每个自动机中)存在具有相同左上下文的轨迹。这是由于 LR(k)的定义导致的。但是当冲突只存在于LALR(1)自动机中,而不在LR(1)自动机时(称这种为LALR独有冲突),则没有相关的轨迹存在。LALR 构造技术的空间节省方面,“合并”两个不同的左上下文,会导致一个冲突。
在第二个场景中,因为我们建议每个贡献项只打印一个归约轨迹,然后打印从开始状态到项的最短路(这些措施减少了体积和归约轨迹的大小),可以构造一个语法,它由一个LALR-独有的冲突和一个不同的 LR 冲突,但是相对的,任意两个已打印的轨迹都没有相同左上下文。然后可能会错误的猜测冲突是 LALR-独有的。
一种避免这种困惑的方式如下:当产生式$p_1,p_2,\cdots,p_n$发生归约-归约冲突时,为 $p_1$ 产生轨迹;然后,对于其它的产生式,只产生与 $p_1$ 轨迹相应的轨迹。如果没有找到相应的轨迹,则查明是 LALR-独有的冲突,就这样报告(然后没有过相应的轨迹需要打印)。但同样的,由于我们对 $p_1$ 的轨迹的有限选择,即使找到 $p_2,\cdots,p_n$ 相关的轨迹,也不一定意味着语法就没有 LALR-独有的冲突。$p_1$ 的其它轨迹(没有打印的),可能会阐明这样的冲突。
但是,如果用户迭代地移除他语法中的轨迹冲突,然后重新提交语法给生成器,被忽略的轨迹最终还是会出现。因此,尽管生成器不一定在单次运行中给出所有的冲突,但是他最终会查明所有的冲突,然后指出它们是 LR 还是 LALR 的。这似乎是一个可以接受的方案,因为用户(和我们)通常一次只能处理少量的冲突。实际上,对于前一子节给出的算法,我们从来没有遇到 LR 归约-归约冲突,没有产生过相关的轨迹。此外,我们只见过一个实际的包含 LALR-独有的冲突的语法,被表明缺乏相关的轨迹。
最好的解决方案是不产生带有 LALR-独有的冲突的自动机。这个由文章[22, p.38] 建议的状态分离的方法可以用于扩展 LALR(1)自动机,因此,它是一个局部的 LALR(1),其中会出现归约-归约冲突(因此任何的 LALR-独有的冲突可以被消除了)。然后,相关的归约轨迹会被找到。LALR 对于普通的翻译写作系统用户太复杂了,以致于要花时间了解–他需要知道 LR 项是什么,如何通过合并项集合构造状态等;所以,纠正LALR-独有的冲突通常是不容易的。
与之相反的,这节给出的轨迹不需要项和项集合并的概念。用户只需要知道解析器解释的输入文本被限制在只向前看一个符号;可以生成查明相同文本(前驱)是如何有两个不同解释的轨迹。任何可以理解LR(k)定义的人都可以理解这个轨迹(假设 LALR-独有的冲突已经被状态-分离移除,能提供相应的归约轨迹)。大部分的 MetaWare翻译书写系统的用户对LR 自动机构造知之甚少或者一无所知的,也有许多不理解LR(k)的定义的;但是他们还是能从使用这些轨迹中获得信息。我们轨迹一个重要的方面是,它们是为人类精心设计的,即,它们通过推导与语法相关,而不是状态或者项。
Kristensen 和 Madsen[18] 给出了,如何通过仅检查 LR(0)自动机,来判断一个语法何时是LR(kj)的(与LALR(k)相比)。他们给出了调试轨迹,可以区分出 LR 和 LALR-独有的冲突。虽然他们的结果理论上是有意思的,但是LALR-独有的轨迹实际中对于通常的翻译书写系统的使用者不是很有用,这是我们之前讨论过的。他们给出的示例轨迹严重地依赖于读者关于 LR 和 LALR 自动机的技术理论,因此,仅使用于在 LR 理论方面受过良好训练的人。
综上,从这节给出的算法,我们可能产生诊断调试轨迹,其可以指出文法中的 LALR-独有 和 LA 冲突。这种轨迹有利于甚至是语法设计新手阅读,它们是任意精心设计的翻译写系统的重要组成部分。
结论
定义了 includes 和 reads 两个关系来获取计算 LALR(1)向前看集问题的基础结构。向前看集计算需要的信息,可以通过图遍历算法的两个后继应用获得,每个关系对应一个。因此,除了基础表示的微小和持续改进,我们觉得这可能是这个问题最好的算法。我们把这个推测的证明和证伪留到了后续的研究中。
给出了 includes 和 reads 关系中的非平凡 SCCs 的特征与语法属性相关联的推论和定理。展示出了这些关系对于打印信息帮助语法设计者在调试非-LALR(1)语法中是有价值的。
最后,流行的 NQLALR 算法被形式化,且被证明是错误的。这些能帮助其他人避免相同的错误。
附录 定理的证明
略。
致谢
略。
引用
略。