一种高效计算单一静态赋值形式的方法
简介
在优化编译器中,数据结构的选择直接影响了实际程序优化的能力和效率。一个糟糕的数据结构选择会禁掉一些优化或者使得编译变慢,则高级优化特性会变得不受欢迎的。最近,静态单一赋值形式 [AWZ88,RWZ88] 和控制依赖图 [FOW87] 被提出用于表示程序的数据流和控制流属性。这些之前不相关的技术每个都为一类有用的程序优化提供了效率和功能。虽然这些结构都很吸引人,但它们的构建难度和它们的潜在大小阻挡了它们的使用[AJ88]。我们提出一种新的算法可以从任意的控制流图中高效计算出这些数据结构。我们给出了分析和实验证明,复杂度与远程程序大小成线性关系。因此,本文强有力的证明了这些数据结构可以实际应用到优化中。
在程序已经转为静态单一赋值形式后,有两个有用的属性:
SSA 形式的前身是通过在程序合适的位置往变量本身插入赋值获得属性 1 的。通过插入显式的 phi 函数,SSA 形式形成了比基于前身的工作方式更简单的工作方式[CLZ86,WZ85]。
属性1 已经被常量折叠算法使用了,它在编译时删除被证明不在使用的代码分支[WZ88]。缺少 SSA 形式时,数据流信息可能不得不在每次代码分支被删除时重新计算,使得算法成本过高。静态单一赋值形式很好的总结了代码移动相关的一些条件[CLZ86,RWZ88]。此外,通过 SSA 形式,简单数据流信息(定点-使用链)的表示更加紧凑。如果一个变量有 D 个定义和 U 个使用,则它们可以有 D*U 个定点-使用链。当类似的信息以 SSA 形式编码时,最多只有 E 个定义-使用链,E 是控制流图边的数量[RL86]。
对属性 2 的开发引出了全局值编号算法,它可以跨控制流追踪冗余计算[RWZ88];和一个检测程序等价的算法[AWZ88]。这边还有一个通过重命名转化增加程序并行度的算法 [CF87b] ,它很像 SSA 的形式。
控制依赖 [FOW87,CF87a] 识别那些影响语句执行的条件。非正式的说,当一个跳转的一条边会导致语句实际上执行,而另一条边会导致语句跳过,则这个语句依赖于这个跳转。这样的信息对于检查并行、程序优化和额外的程序分析[HPR88] 是十分重要的 [ABC88],
第二节解释了 SSA 形式。第三节引入一个新的结构叫做支配边界。然后,我们展示如何使用支配边界高效地计算 SSA 形式(第四节)和控制依赖图(第五节)。第六节展现了我们的算法行为在一些严格限制某些控制结构的程序里与程序大小成线性关系的。我们也通过报告 FORTRAN 程序的实验给出了大部分线性的证明。
静态单一赋值形式
本文介绍的算法适用于含有任意控制结构的程序。在这样的程序中语句被限制为条件表达式和赋值语句。只考虑简单、无别名的变量;没有考虑数组或者指针值。对齐在 [WZ88] 中的技术容下了。
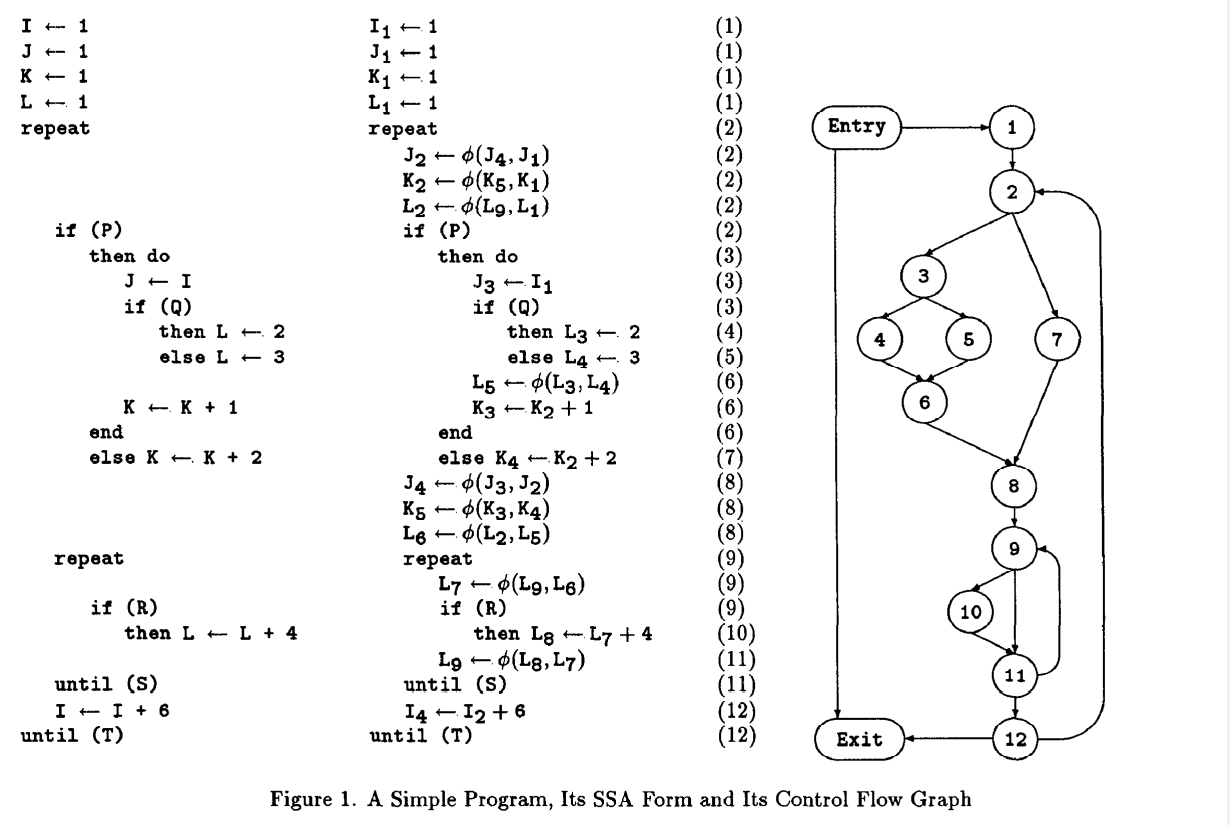
将一个程序转为静态单赋值(SSA)形式分为两步。第一步,特殊的赋值语句 phi 函数插入程序的某些点上。第二步,每个变量 V 用不同的整数 i 赋予几个新的名字 Vi。程序中每个提到的 V 都被替换为提到的新的名字之一 Vi。一个简单程序的 SSA 的形式如图 1 所示。
在详细解释 SSA 形式前,我们用有向图回顾了程序控制流的建模。程序的语句被组织为(不必要最大化)基本块,它表示程序流从第一条语句进入基本块,然后从最后一条语句离开基本块。图 1 中的基本块由括号中的数字列表示。控制流图或者 CFG 是有向无环图。CFG 的节点是程序的基本块和两个额外的节点:入口和出口。从入口有边能到任意程序可以进入的基本块。任意可以推出程序的基本块都有边到达出口。CFG 其它的边表示基础块间的控制转移(跳转)。我们假设每个节点都在从入口开始的路径上,也在每个去出口的路径上。
对于每个节点 X,X 的后继是指 CFG 中有一条 X->Y 的边,然后 Succ(X) 表示的是 X 的所有后继的集合(前驱也是类似的)。我们例子程序的控制流图在图 1 中的右边给出了。由于与控制依赖表示相关的技术原因,图中有从入口到出口的边。最后,每个变量被默认为在入口时有个赋值,表示在程序进入时变量可能具有任意值。这个赋值被视为与代码中显式出现的赋值一样。
一个 phi 函数有公式 U <- phi(V, W, …),其中,U,V,W,… 是变量,V,W,… 等操作数的数量是 phi 函数存在点的控制流前驱的个数。程序中每个点的控制流前驱是以任意固定顺序排列的,且 phi 函数中的第 j 个操作数关联第 j 个前驱,如果控制从第 j 个前驱到达 phi 函数,则 U 被赋予第 j 个操作数的值。phi 函数的每次执行只会使用其中一个操作数,至于使用哪个取决于 phi 函数前的控制流。
对于任意的变量 V,可以在程序的任意 CFG 节点入口插入一个简单的 phi 函数 V <- phi(V, V, …),不会改变语义。为什么我们要执行这样的插入?通过小心放置插入的位置,然后重命名 V 的子项,我们可以将程序转为 SSA 的形式。具体来说,我们假定任意数量的新变量 Vi(i = 0,1,2,…)都可以生成做为 V 的新名字。如果转换后的程序被定义为 SSA 的形式,对于每个原始变量 V,V 的 phi 函数已经插入,然后 V 的每个使用都被改成了一个新名字 Vi 的使用,使得如下条件成立:
- 如果一个 CFG 节点 Z 是两个非空路径 X->Z 和 Y->Z 共有的第一个节点,在 X 节点和 Y 节点的开头都包含 V 的赋值,则 V 的一个 phi 函数被插入到 Z 的开头。
- V 的每个新名字 Vi 是程序代码中一个确定赋值语句的赋值目标。
- 沿着每个控制流路径,考虑每个 V 使用新的名字 Vi (在转换后的程序中)和 V 的相应使用(在原始程序中)。然后 V 和 Vi 有相同的值。
当一个程序是 SSA 形式且插入的 phi 函数的数量尽可能的小,则它是最小 SSA 形式。
依赖于 SSA 形式的优化在有无关 phi 函数存在时,仍然是有效的, 除了那些需要最小 SSA 形式的。无关 phi 函数有些时候会通过隐瞒一些有用事实禁止优化;无关 phi 函数总是加入了一些不必要的固有开销到优化本身。因此,只放置需要的phi 节点是重要的。
对于任意的变量 V,源程序中我们需要插入 phi 函数的 CFG 节点可以通过 SSA 形式定义中的第一个条件递归定义。当那些两个路径源自不同的节点,包含 V 的赋值或者需要 V 的phi 函数,如果节点 Z 是两个非空控制流路径的共有节点,则 Z 需要一个 V 的 phi 函数。非递归地,我们可能或观察到一个节点 Z 需要 V 的 phi 函数,因为 Z 是从带有 V 赋值的节点 X 和 节点 Y 开始的两个非空路径 X->Z 和 Y->Z 的第一个共有节点。如果 Z 不是包含了已经包含了一个到 V 的赋值,则在 Z 插入 phi 函数,然后将 Z 加入到 V 的赋值节点集合里。当有更多的节点被认为是路径源时,我们可能会观察到更多的节点作为两个非空路径的第一个节点,节点开头有 V 的赋值。观察到需要 phi 函数的节点集合会一直增加直到它稳定。当 phi 函数以这样的方式放置时,可以通过一个简单自适应的大家熟知的 def-use 链来获得一个最小的 SSA 形式。本文提出的算法与暴力方式得到的结果相同,但放置 phi 函数和进行重命名的时间远小于暴力需要的时间。
最小化 SSA 形式是 Shapiro 和 Saint [SS70] 伪赋值概念的一种改进。V 的伪赋值节点就是那些需要 V phi 函数的节点。对于一个有 E 条边的 CFG ,其描述了一个调用 V 变量的程序,一个算法 [RT82] 需要 O(Ea(E))个位向量操作(每个向量长度为 V)来找到所有的伪赋值。对于可约束程序计算 SSA 形式的更简单算法需要 O(E x V)的时间。这些算法都是二次的,且 [RWZ88] 算法会使用一些无关的 phi 函数。这边提到的方法是 O(E+T+DF)的,其中 T 是普通的赋值和 phi 函数的总数,DF 是所有支配边界的总大小(我们后面会描述这个结构)。虽然数量 T 和 DT 可能是程序大小的二次方,但我们提供证据证明它们很少如此。这个见解允许我们得到一个不会随变量数量乘法增长的边界,其是一个我们可以根据支配边界决定哪边可以插入 phi 函数的时间边界。支配边界的大小只依赖于程序的控制流。
支配边界
这节中我们引入支配边界映射,然后给出一个计算它的算法。然后,我们将 phi 函数的正确位置和支配边界关联起来。
在进行前,我们回顾下控制流中节点间的支配关系。令 X 和 Y 为 CFG 中的节点。如果 X 出现在所有到达 Y 的路径上,则 X 支配 Y。支配既是自反的又是传递的。如果 X 支配 Y 且 $X \not= Y$ ,则 X 严格支配 Y。公式上,严格支配我们写为 $X \gg Y$ ,支配写为 $X\ge\ge Y$ 。为了说 X 没有严格支配 Y,我们写作 $X\not\gg Y$ 。Y的立即支配(表示为 idom(Y))是从 Entry 到 Y 的任意路径上 Y 最接近的严格支配者。在一个支配树上,节点 X 的子节点都是被 X 立即支配的。设 E 是 CFG 中边的数量。CFG 的支配树可以在 $ O(E\alpha(E))$ 时间里构建 [LT79],或者(用更复杂的算法)在 $O(E)$ 时间里构建[Har85]。
CFG 的支配树有和 CFG 完全相同的节点集,但边集完全不同。这边的前驱,后继,和路径总是和 CFG 相关的。而父节点,子节点,祖先节点,和后裔节点总是和支配树相关的。
定义和算法
一个 CFG 节点 X 的支配边界 $DF(X)$ 是所有满足条件的 CFG 节点 Y,对应的条件是 X 支配 Y 的前驱,但不是严格支配 Y 的:
$$
DF(X) = {Y | (\exists P \in Pred(Y))(X\geq\geq P 且 X \not\gg Y)}.
$$
直接根据定义计算 $DF(X)$ 需要搜索支配树的大部分。所有节点 X 计算 $DF(X)$ 总时间将会是二次方的,即使计算集合很小。为了在支配边界映射大小相关的线性时间里计算支配边界映射,我们为每个节点定义了两个中间集 $DF_local$ 和 $DF_up $ ,然后保持下面的方程:
$$
DF(X) = DF_local(X)\cup \bigcup_{Z\in Children(X)} DF_{up}(Z). (1)
$$
对于任意节点 X,X 的一些后继会有助于 $DF(X)$。局部贡献 $DF_{local}(X)$ 按如下定义
$$
DF_{local}(X) = {Y\in Succ(X) | X \not\gg Y}.
$$
给定任意的节点 Z,它不是支配树的根入口,对于 $ X = idom(Z)$,$DF(Z)$ 中的一些节点会贡献给 $DF(X)$。贡献 $DF_{up}(Z)$ ,Z 传给 $idom(Z)$ 按如下定义:
$$
DF_{up}(Z) = {Y\in DF(Z) | idom(Z) \not\gg Y}.
$$
引理 1 支配边界公式(1)是正确的。
证明 因为支配总是反身的,$DF_{local}(X) \subseteq DF(X)$。因为支配是及物的,X 的每个子节点 Z 有 $DF_{up}(Z) \subseteq DF(X)$。我们仍然必须证明 $DF(X)$ 中的所有东西都已经计算在内了。假设 $Y \in DF(X)$,然后令 $U\to Y$ 是一个 X 支配 U 但不严格支配 Y的边。如果 $ U = X$,然后 $ Y \in DF_{local}(X)$ 证明结束。如果 $U \neq X$,换句话说 X 的子节点 Z 支配 U 但不严格支配 Y,因为 X 不严格支配 Y。这隐含着 $Y\in DF_{up}(Z)$。
中间集可以用如下简单的相等测试计算。
引理 2 对于任意的节点 X,
$$
DF_{local}(X) = {Y \in Succ(X) | idom(Y) \neq X }.
$$
证明 我们假设 $Y\in Succ(X)$ 然后有:
$$
(X \gg Y) \Longleftrightarrow (idom(Y) = X).
$$
“if” 的部分是真的,因为严格支配是立即支配的传递闭包。对于 “only if” 的部分,假设 X 严格支配 Y,因此 X 的一些子节点 V 支配 Y。然后 V 出现在任意从入口到 Y 的路径上,到达 X,然后有边 $ X\rightarrow Y$,则有 V 支配 X,或 $ V = Y$。但是 V 不支配 X,所以 $V = Y$ 和 $ idom(Y) = idom(V) = X$。
引理 3 对于支配树里的任意的节点 X 和 X 的任意子节点 Z,
$$
DF_{up}(Z) = {Y\in DF(Z) | idom(Y) \not\gg X}.
$$
证明 我们假设 $Y\in DF(Z)$ 有如下
$$
(X \gg Y) \Longleftrightarrow (idom(Y) = X).
$$
“if” 的部分是真的,因为严格支配是立即支配的传递闭包。对于 “only if” 的部分,假设 X 严格支配 Y,因此 X 的一些子节点 V 支配 Y。选择一个 Y 的前驱 U,Z 支配 U。然后 V 出现在任意从入口到 Y 的路径上,到达 U,然后有边 $ U\rightarrow Y$,则有 V 支配 X,或 $ V = Y$。如果$ V = Y$,则 $ idom(Y) = idom(V) = X$,然后证明结束。我们假设 $V \neq Y$(因此 V 支配 U)则有个矛盾。只有一个 X 的子节点可以支配 U,所以 $V = Z$ 且 Z 支配 Y。这与 $Y\in DF(Z)$ 的假设相矛盾。
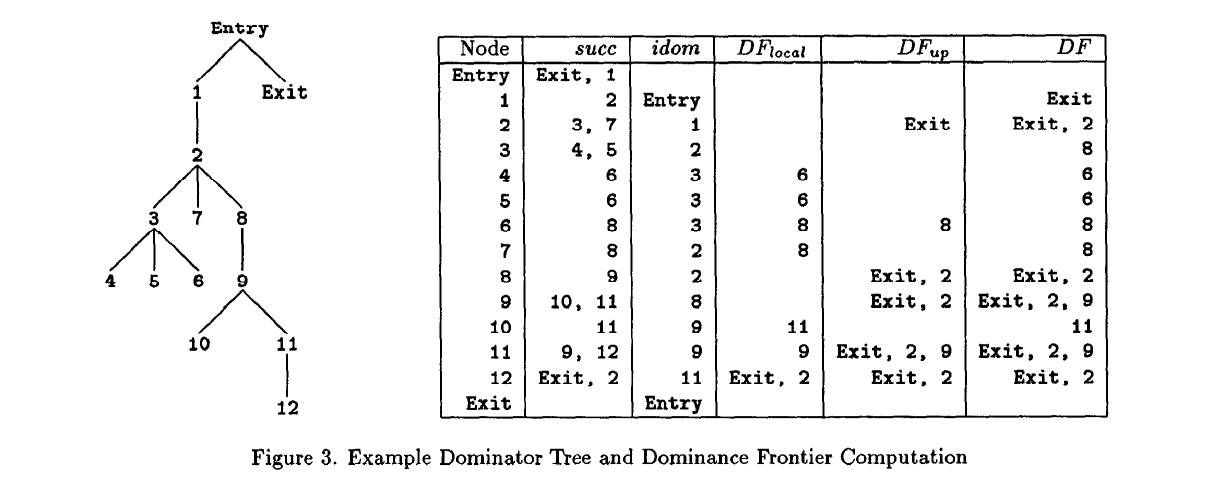
这些结果暗示了图 2 中的计算支配边界的算法是正确的。/*local*/ 所在行高效的实时地计算了$DF_{local}(X)$ 然后在(1)中使用它,不需要额外的存储它。/*up*/ 对于 $DF_{up}(Z)$ 是相似的。我们自底向上遍历支配树,在访问完 X 的所有子节点后访问 X。为了说明这个算法的工作过程,我们在 图 3 中列出结果,其中的 CFG 是来自 图 1 中的程序。

定理 1 图 2 中的算法是正确的。
证明 由前面的定理得到。
考虑一个有 N 个节点和 E 条边的 CFG。支配边界算法在计算$DF_{local}$时,最终会检查所有的 CFG 边。计算 $DF_{up}$ (最糟糕的时候)需要在支配树间传播 N 个节点。计算 $DF_{up}$ 以及 DF 需要的时间是和 $DF_{up}$ 成比例的。因为支配树有 $N-1$ 条边,计算用时$O(N^2)$。因此,整个算法的最坏复杂度是$O(E+N^2)$。但是,第六节表明通常 DF 映射大小通常是线性的。我们实现了这个算法,观察到它比 PTRAN 编译器里计算标准数据流要快[ABC88]。
使用支配边界找需要的 $\phi$ 函数
我们从更正式地重述 $\phi$ 函数插入位置的非递归特性开始。对于 CFG 节点的一个集合 S,连接节点集合 $J^+(S)$ 被定义为所有 Z 节点的集合,Z 是两个开始与 S 中两个清楚节点的非空 CFG 路径的第一个公共节点。迭代添加$J(S)$ 是节点递增序列的极限:
$$
J_1 = J(S);
$$
$$
J_{i+1} = J(S\cup J_i)
$$
尤其,如果 S 碰巧是变量 V 的赋值节点集,则 $J^+(S)$ 是 V 的 $\phi$ 函数节点集。
连接和迭代连接操作将节点集映射到节点集。我们以自然的方式延长支配边界的映射从节点到节点集:
$$
DF(S) = \bigcup_{X\in S} DF(X).
$$
与加入一样,迭代支配边界 $DF^+(S)$ 是节点集递增子序列的极限
$$
DF_1 = DF(S);
$$
$$
DF_{i + 1} = DF(S \cup DF_i).
$$
$DF^+(S)$ 的实际计算是通过一个高效地工作链表进行的;这边的公式便于将迭代支配边界和迭代连接关联在一起。如果 S 碰巧是变量 V 的赋值节点集,则我们会看到:
$$
J^+(S) = DF^+(S)
$$
因此,变量 V 的 $\phi$ 函数的位置可以通过计算 $DF^+(S)$ 的工作链表算法来计算,其在第 4 节给出了。
下面的引理通过关联支配边界到连接上,做了许多的工作。
引理 4 对于任意非空路径 p:$X\to Z$ 在 CFG 中,有 p 上一个节点 $X^{‘} \in {X} \cup DF({X}) $ 支配了 Z。
证明 令 $X’$ 是 p 上 ${X} \cup DF({X})$ 的最后一个节点。我们假设 $X’$ 不支配 Z ,则衍生了一个矛盾。因为支配是反身的,$X’ \neq Z$ 且在 p 上的 X’ 之后有第一个节点 Y,使得 X’ 不支配 Y。p 上 Y 的前驱被 X’ 支配,所以
$$
Y\in DF(X’) \subseteq DF({X} \cup DF({X})) = DF({X}),
$$
这与 X’ 的选择冲突。
引理 5 令 $X\neq Y$ 是 CFG 上的两个节点,假设在 CFG 上的两个非空路径 p:$ X\rightarrow Z$ 且 q:$ Y\rightarrow Z$ ,Z 是公共的第一个节点。然后 $Z\in DF({X}) \cup DF({Y})$。
证明 我们从引入一个假设 $Z \neq X$ 和 $Z \neq Y$ 开始证明这个引理。令 X’ 来自引理 4 的路径 p。令 Y’ 来自引理 4 的路径 q。让 p’ 和 q’ 相应为 p ,q 最后的片段。任何沿着 q’ 从入口到 Y’ 在到 Z 的路径必须包含 X’,但是 Z 是 q‘ 中唯一位于 p 的点。因此
$$
X’ \geq\geq Y’ 或者 X’ = Z.
$$
相似的,
$$
X’ \geq\geq Y’ 或者 Y’ = Z.
$$
因为 $X’$ 和 $Y’$ 不能相互支配,它们中的一个必须是 $Z$ 。我们可以假设 $X’ = Z$ ,因此 $ Z \in {X} \cup DF({X})$。但是 $Z\neq X$,所以 $Z \in DF({X}) \subseteq DF({X}) \cup DF({Y})$。
现在假设 $Z$ 是 $X, Y$ 中的一个。我们可能会假设$Z = X$,则相应的 $Z \neq Y$。如果沿着 p 的第一条边是 $Z\rightarrow Z$,则 $Z\in DF({Z}) \subseteq DF({X})$ ,我们完成工作。另一个假设沿着 p 的第一条边是 $Z \rightarrow A \neq Z$。我们可以将上一段应用到路径 a 和 q 上,其中 a 是 $Z \rightarrow A$ 之后 p 的剩余部分。我们像前一段的 $X’$ 和 $Y’$ 一样获得 $A’$ 和 $Y’$,如
$$
A’ \geq\geq Y’ 或者 A’ = Z.\ \ \ \ \ (2)
$$
$$
Y’ \geq\geq A’ 或者 Y’ = Z.\ \ \ \ \ (3)
$$
如果 $Y’ = Z$,则我们像之前一样继续使用 $Z \neq Y$ ,派生出 $Z\in DF^+({Y})$。替换假设为 $Y’\neq Z$,则 (3) 隐含了 $Y’ \geq\geq A’$ ,且 (2) 隐含了 $A’ = Z$。但是 $A’\in {A} \cup DF({A})$,则 a 中存在节点序列 $A = A_0,…,A_L = Z$,对于每个 i 有 $A_{i + 1}\in DF(A_i)$ 且 $A_i$ 支配 a 上在 $A_i$ 之后 ,$A_{i+1}$ 之前的任意节点。归纳到 i,我i们有
$$
A_i \in DF^+({Z}) 或 Z \geq\geq A_i\ \ \ \ \ (4)
$$
尤其,对于$i = L -1 $,我们发现 $A_i$ 支配 a 上 Z 的前驱,满足 (4)。在两个场景下,$Z\in DF({Z}) = DF({X})$。
引理 6 对于 CFG 节点的任意集合 S,$J(S) \subseteq DF^+(S)$。
证明,我们应用引理 5.
引理 7 对于 CFG 的任意集合 S,$Entry \in S$,有$DF(S)\subseteq J(S)$ 。
证明,对于任意 $X \in S$ 和任意 $Y\in DF(X)$。有一个从 X 到 Y 的路径,其中在 Y 之前的所有节点都被 X 支配。同时也有一条从 Entry 到 Y 的路径,其中所有的节点都没有被 X 支配。因此,两条路径共有的第一个节点是 Y。
定理 2 对于任意变量 V 需要 $\phi-函数$ 的节点的集合是迭代支配边界 $DF(S)$,其中 S 是 V 的赋值集合。
证明,V 需要$\phi-函数$的节点集合是$J(S)$。由引理 6 和对 J 定义中 i 的归纳,我们有
$$
J^+(S) \subseteq DF^+(S).
$$
归纳步骤如下:
$$
J_{i+1} = J(S\cup J_i) \subseteq J(S\cup DF(S)) \subseteq DF^+(S\cup DF^+(S)) = DF^+(S).
$$
Entry 节点在 S 中,所以引理 7 有另一个归纳
$$
DF^+(S) \subseteq J^+(S).
$$
最小SSA形式构建
图 4 的算法是用于插入琐碎$\phi-$函数的。对于程序中的每个变量,算法的外循环只执行一次。使用的数据结构有:
- W 是一个正在处理的 CFG 节点的工作列表。这个算法的每次迭代,W 被初始化为包含赋值到 V 的节点的集合 $A(V)$。每个迭代在工作列表为空的时候结束。
- Work(\)* 是标志数组,一个节点一个标志,如果 X 曾经被添加到 W,则 $Work(X)$ 是 1。在每次迭代中,每个节点都可能且只有一次被添加到 W。
- DomFornPlus(\)* 是标志数组,一个节点一个标志,当 V 的 $\phi-$函数已经被插入 X,则 $DomFronPlus(X)$被置为 1。在每次迭代结束的时候,$DomFronPlus(X) = 1$ 的节点 X 就是 $A(V)$ 的迭代支配边界的节点。

图 4 中处理单个变量需要的时间,与普通赋值和$\phi-$函数两者总数加上相关的支配边界关系总数的和成正比。
图 5 的算法重命名了在深度优先搜索访问支配树节点中遇到的所有变量。新的命名表示为$V_i$,i 是整数,为每个变量都生成。搜索从入口开始,此时变量 V 的入口值通过一个有空右侧的赋值表示。在这边重命名每个 V 到 $V_0$ 之后,搜索继续移动到其它节点。一个处理语句的节点访问与节点的排列顺序相关,从任意一个可能已经被插入的$\phi-$函数开始。语句处理过程只需要针对语句中实际提到的变量进行。与图 4 对比,当我们初始化如下数据结构的两个数组时,我们只需要所有变量一次:
$S(*)$ 是栈的数组,每个变量 V 一个栈,栈保存整数。$S(V)$ 顶部的整数 i 用于构造变量名$V_i$,其用于替换 V 的使用。
$C(*)$ 是整数的数组,每个变量 V 一个数,计数值 $C(V)$ 表明有多少 V 已经被处理了。
$WhichPred(Y,X)$ 是整数,用于说明 CFG 中 Y 的哪个前驱是 X。Y 的 $\phi-$ 函数的第 j 个操作数与来自 Y 的边的列表的第 j 个前驱关联。
每个赋值语句 A 有如下形式
$$
LHS(A)\leftarrow RHS(A)
$$
其中右侧部分 $RHS(A)$ 是一个表达式,左侧$LHS(A)$ 是目标变量 V。重命名后已经将 V 替换为 $V_i$ 作为目标,老的目标仍然被记录为 $oldLHS(A)$。

下一个引理表明,对于转换程序的一个变量,将“The”赋值变成一个新的名字是合理的。
引理 8 转换程序提到的每个新名字$V_i$ 是一个确切赋值的目标。
证明,因为计数器 $C(V)$ 在处理每个赋值给 V 都自增,可以且只有一次赋值给$V_i$。因为$V_i$的任意使用都有$i = Top(S(V))$ V被替换为$V_i$,其中至少有一个赋值给$V_i$。
对于每个变量 V 和 CFG 节点 X,在$SEARCH(X)$ 的第一个循环结束时,我们可以根据$S(V)$的栈顶关联 V 的名字$TopAfter(V,X)$。特别的,
$$
TopAfter(V, X) = V_i \ \ 其中 i = Top(S(V))
$$
如果 X 的子节点 Y 没有 V 的$\phi-$函数,则 Y 中 V 的第一次使用(任意)被替换成 $TopAfter(V,X)$ 的使用。因此 Y 从它的父节点 $X = idom(Y)$ 继承了 V 的名字。另一方面,CFG 中 Y 的任意前驱 P 确定一个名字 $TopAfter(V, P)$ ,与转换后的程序是否和源程序等价的问题,有明显的相关性。幸运的时是,候选名字间是没有冲突的。
引理 9 对于任意的变量 V 和任意的 CFG 边 $P\rightarrow Y$ ,满足如下公式时,使得 Y 没有 V 的 $\phi-$函数,
$$
TopAfter(V, P) = TopAfter(V, idom(V)). \ \ \ \ (5)
$$
证明,我们会假设$P \neq idom(Y)$。因为 Y 没有 V 的$\phi-$函数,如果一个节点 X 有$Y\in DF(X)$,则 X 不会赋值给 V 的一个名字。我们在下面两次使用了这个事实。
通过引理 2,$Y\in DF_local(P) \subseteq DF(P)$ 和 P不赋值给 V 的一个名字。令 Y 是赋值给 V 的序列 $idom(P), idom(P), …$ 的第一个节点。然后
$$
TopAfter(V, P) = TopAfter(V, U). \ \ \ \ (6)
$$
因为 U 赋值给 V 的一个名字,$Y \not\in DF(U)$。但是 U 支配 Y 的一个前驱,所以 U 严格支配 Y。对于 $U \gg X \geq\geq idom(Y)$ 的任意 X,我们有 $X \geq\geq P$,因为$X \gg Y$。通过 U 的选择,$U \gg X \geq\geq P$ 隐含了 X 不会赋值给 V 的一个名字。因此
$$
TopAfter(V, U) = TopAfter(V, idom(Y)).
$$
且(5)伴随着(6)。
引理 10 考虑转换后程序的任意控制流路径和对应源程序中的路径。对于沿着路径遇到的任意的变量 V 和任意的边$X \rightarrow Y$ ,在源程序中从 X 流向到 Y 的 V 的值,等价于已转换程序中从 X 流向 Y 的 $TopAfter(V, X)$ 的值。
证明,我们沿着路径进行归纳,在入口每个输入值赋值之后,以 $V = V_0$ 开始。为了继续归纳,考虑沿着路径上的任意连续的边$X\rightarrow Y \rightarrow Z$,令 $j = WhichPred(Y, X)$。我们假设$V = TopAfter(V, X)$ 沿着第一条边,然后显然有 $V = TopAfter(V, Y)$ 沿着第二条边。
如果 V 在 Y 中有$\phi-$函数,则 $\phi$ 的第 j 个操作数是$TopAfter(V, X)$ 且已转换程序的$\phi-$函数的目标是接受 V 的值。如果 V 在 Y 中没有$\phi - $ 函数,则引理 9 已证。在两个场景下,V 的正确值在定义了 Y 的普通代码的基本块开头就是有效的了。在基本块里,已转换函数的控制流与 SEARCH的第一个循环处理的语句序列是相同的。对于每个变量 V,我们确实有$V = TopAfter(V, Y)$ 沿着第二条边。
定理 3 通过应用图 4 中的算法以及图 5 的算法,任意的程序都可以转为最小化的 SSA 形式。
证明,图 4 将 V 的 $\phi$ 函数放入迭代支配边界 $DF^+(S)$ 的节点中,S 是源程序中赋值给 V 的集合。通过定理 2,$DF^+(S)$ 是 V 需要$\phi-$函数的节点的集合,所以我们获得了 SSA 定义中最少 $\phi-$函数的条件 1。
我们仍然必须表明图 5 做了正确的重命名。SSA 形式定义中的条件 2 来自引理 8。SSA 形式定义中的条件 3 来自引理 10。
控制依赖的构造
在这节中我们表明控制依赖[FOW87]本质上是控制流图的逆转图上的支配边界。令 X 和 Y 是 CFG 的节点。如果 X 出现在从 Y 到 Exit 的任意路径上,则 X 后支配 Y。如同支配关系,后支配关系是自反和及物的。如果 X 后支配 Y 但 $X\neq Y$,则 X 严格后支配 Y。Y 的立即后支配者是任意从 Y 到 Exit 的路径上 Y 的最近严格后支配者。在一个后支配树上,X 节点的子节点都是被 X 立即后支配的。
一个 CFG 节点 Y 是控制依赖于一个 CFG 节点 X 的,当保有如下两个规则:
- 有一个非空路径 p:$X\rightarrow^+ Y$,其中 p 上 Y 后支配 X 之后的任意节点。
- 节点 Y 不是严格后支配节点 X 的。
这边我们使用的控制依赖的定义可以证明和原来使用初等一阶逻辑的定义[FOW87]是等价的。
引理 11 令 X 和 Y 是 CFG 的节点。则当且仅当一个非空路径$p: X\rightarrow^+ Y$ ,Y 后支配 p 上 X 之后的每个节点时,Y 后支配 X 的后继。
证明,假设 Y 后支配 X 的一个后继 U。选择任意从 U 到 Exit 的路径 q。然后 Y 出现在 q 上。令 r 是 q 的初始段,其能达到 q 上第一个出现的 Y。对于 r 上任意节点 V,通过跟随 r 到 V,我们可以获得 U 到 Exit,然后获得任意 V 到 Exit 的路径。因为 Y 后支配 U,但不存在 r 的结尾之前,Y 也必须后支配 V。令 p 是开始于边$X\rightarrow U$的边,然后沿着 r 前进。则$p: X\rightarrow^+ Y$ 且 Y 后支配 p 上 X 之后的任意节点。
反过来,给定具有这些属性的路径 p,令 U 是 p 上 X 之后的第一个节点。则 U 是 X 的后继且 Y 后支配 U。
逆控制流图 RCFG 具有与给定控制流图 CFG 相同的节点,但对于 CFG 中每条边 $X\rightarrow Y$ 都有 $Y\rightarrow X$。Entry 和 Exit 的角色也被反转。CFG 的后支配关系等同于 RCFG 上的支配关系。
推论 1 令 X 和 Y是 CFG 上的节点。则当且仅当 RCFG 中$X\in DF(Y)$ 时,CFG 中的 Y 控制依赖于 X。
证明,使用引理 11 来简化控制依赖定义中的第一条件,我们发现当且仅当 Y 后支配 X 的后继但不严格支配 X 时,Y 控制依赖于 X。在 RCFG 中,可以说成 Y 支配于 X 的前驱但不严格支配 X,即,$X \in DF(Y)$。
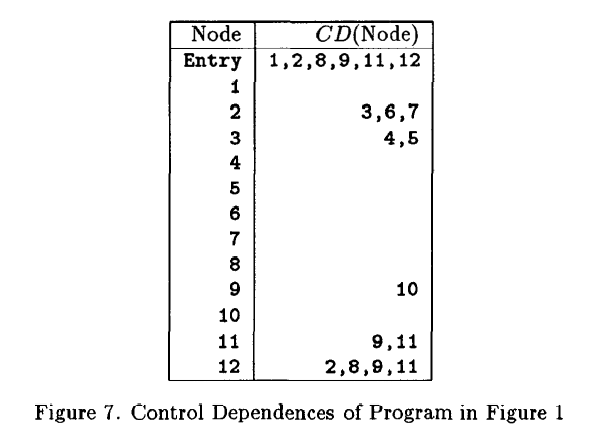
图 6 应用这个规则来计算控制依赖。通过应用图 6 中的算法到图 1 的控制流图,我们获得图 7 的控制依赖。我们重标记从入口到出口的边,加入到 CFG,因此控制依赖关系,被视为一个图,根是 Entry。

现在我们把之前的计算控制依赖的工作与我们新的算法进行比较。控制依赖在 [FOW87] 中计算,但是算法如声明使用了二次空间来保存中间计算和多次遍历支配树的过程。我们算法一个更早期的版本 [CF87b] 是为控制依赖制定的,不涉及于支配边界的其它使用。控制依赖也在 [HPR88] 中计算,但是仅限用于经典的结构化编程结构的程序。
分析和测量
对于包含变量 V 的$\phi-$函数的节点的数量是程序控制流结构和 V 赋值的函数。程序结构独自确定了支配边界和控制依赖弧的数量,对于一些程序存在支配边界可能大于计算$\phi-$函数位置所需的,因为实际赋值没有被计算进去。在这节中,我们证明,当控制流分支限制为 if-then-else 结构和 while-do 循环时,支配边界的大小线性于程序的大小。这样的程序可以通过图 8 给与的语法描述。我们也给出实验的结果表明对于实际的程序确实时线性的。

定理 4 对于包含直线代码,if-then-else 和 while-do 结构的程序,任意 CFG 节点的支配边界最多包含两个节点。
证明,考虑一个使用图 8 中语法的自上而下解析的程序。初始时,在解析树撒谎给你我们有个简单的
(1) 这个生成式添加了一个 CFG 节点 S 和边 $Entyr \rightarrow S \rightarrow Exit$,产生$DF(S) = {Exit}$。
(2)当这个生成被应用时,一个 CFG 节点 S 被替换成两个节点 $S_1$ 和 $S_2$。之前进入和离开 S 的边,现在进入 $S_1$,离开 $S_2$。一个单边被插入到 $S_1$ 到 $S_2$ 的地方。虽然控制流图已经改变,考虑这个过程如何影响支配树。节点 $S_1$ 和 $S_2$ 支配了所有被 S 支配的节点。此外,$S_1$ 支配了 $S_2$。因此,我们有$DF(S_1) = DF(S) = DF(S_2)$。
(3)当这个生成式被应用时,一个 CFG 节点 S 被替换成节点$T_{if}, S_{then}, S_{else}$ 和 $T_{endif}$。之前进入和离开 S 的边,现在进入$T_{if}$,离开$T_{endif}$。 边被插入到从 $T_{if}$ 到 $S_{then}$ 和 $S_{else}$ 中;或者边也被插入到从$S_{then}$ 到$S_{else}$ 和$T_{endif}$间。在支配树上,$T_{if}$ 和 $T_{endif}$ 都支配了所有被 S 支配的节点。此外,$T_{if}$ 支配了$S_{then}$ 和$S_{else}$。由为产生式(2)生成的参数,我们有$DF(T_{if}) = DF(S) = DF(T_{endif})$ 。现在考虑节点$S_{then}$ 和$S_{else}$。从支配边界的定义,我们获得$DF(S_{then}) = DF(S_{else}) = {T_{endif}}$。
(4)当这个生成式被应用时,一个 CFG 节点 S 被替换成节点$T_{while}$ 和$S_{do}$。之前所有关联到 S 的边,现在都关联到$T_{while}$。边被插入到从$T_{while}$ 到$S_{do}$ 和从$S_{do}$ 到$T_{while}$ 之间。节点$T_{while}$ 支配所有被 S 支配的节点。因此,我们有$DF(while) = DF(S) \cup {T_{while}}$ 和$DF(S_{do}) = {T_{while}}$。
(5)在应用了这个生成式后,新的控制流图与老的是同构了。
因此,每个生成式都会导致一个 CFG 节点被替换成新的子图。在新的子图中,只有$T_{while}$ 节点在它的支配边界上可能有超过一个节点。这样的节点不会被展开成子图,所以最后的 CFG 上的每个节点在它的支配边界上最多有两个节点。
推论 2 对于包含直线代码,if-then-else 和 while-do 结构的程序,每个节点最多控制依赖两个节点。
证明,考虑一个包含所有允许结构的程序 P,和它关联的控制流图 CFG。逆控制流图 RCFG 本身就是一些程序$P’$ 的结构化控制流图。对于 RCFG 上的所有 Y,根据定理4 $DF(Y)$ 最多包含两个节点。通过推论 1,则 Y 最多控制依赖两个节点。
不幸地是,这些线性结果不是对所有的程序结构都能保持的。特别是,考虑到图 1 中的示例的内层 repeat-until 循环。对于每个循环,循环里的节点的支配边界包含了每个到环绕循环的入口。对于第 n 层循环,这会导致支配边界映射的整个总大小是$\theta(n^2)$,同时每个变量需要最多$O(n)$个$\phi-$函数。大部分的支配边界映射并不都是实际用于替换$\phi-$函数的,故这边有个担忧是,相对于实际$\phi-$函数的结果数量,支配边界的计算可能花费了过多的时间。因此,我们希望测量支配边界节点数量和程序函数大小,会覆盖各种各样的程序集。
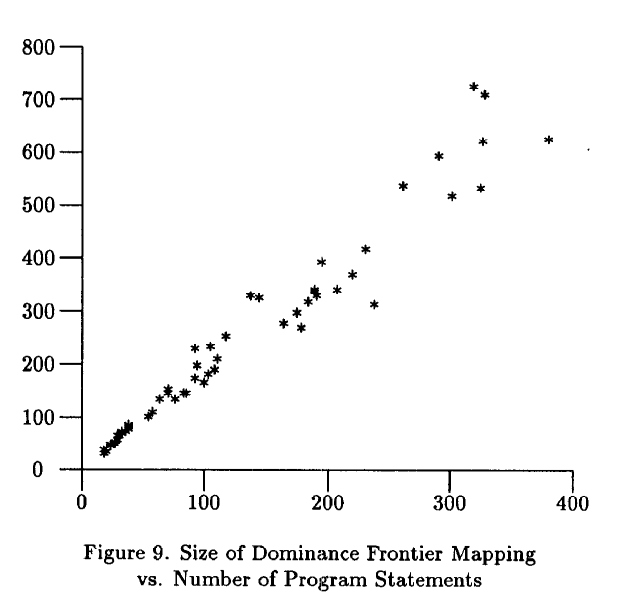
在 EISPACK[SBD76] 上,我们实现了我们的支配边界算法,并用来执行 FORTRAN 程序。我们之所以选择这些例程,是因为它们包含不可约区间和其它非结构化构造。我们也在 PTRAN 系统上实现了我们的算法,其已经提供了需要的数据流和控制流分析[ABC88]。对于我们测试的 61 个程序,支配边界弧比起程序大小的比率是从 1.3 到 2.4 的。如图 9 的坐标图显示的,支配边界映射的大小非常线性与程序大小。
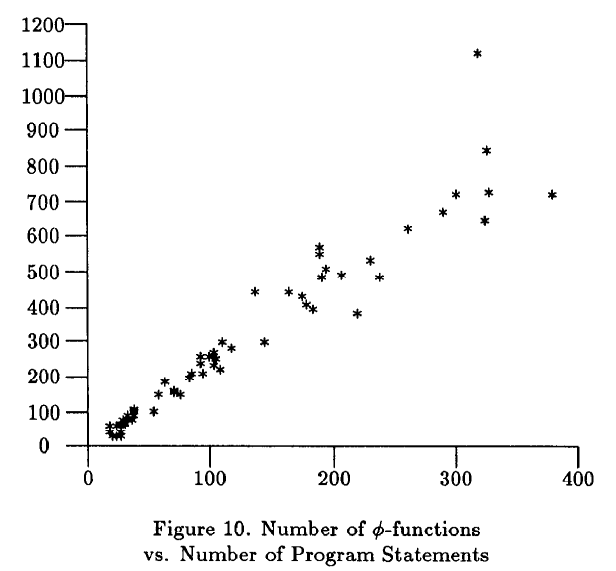
我们下一个关心的是$\phi-$函数的数量与源程序的大小是非线性的。对于我们测试过的程序,图 10 的坐标图确认了$\phi-$函数和相关程序大小是线性相关的。
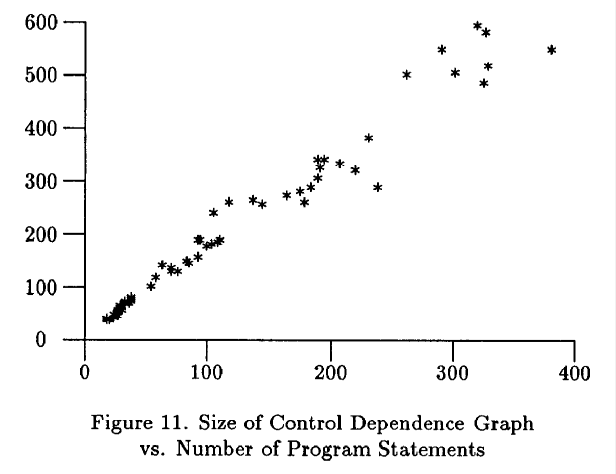
最后关心的是控制依赖图可能与源程序大小是非线性的。对于我们测试过的程序,图 11 的坐标图确认了控制依赖弧和相关程序大小的线性行为。
比较图 9 和图 11,相同的程序集比起生成的控制依赖关系,生成更多的支配边界关系。非正式的,支配边界关系是由于控制图中的连接,但是控制依赖关系来自于控制流图的分叉。我们测试集普遍的编程风格导致了控制流图中的一些节点有高的入度,同时,大部分节点有低的出度。
结论
目前之前的一些工作表明,SSA 形式和控制依赖可以支持强大的代码优化算法,这些优化算法在转换成这种形式后,基于程序大小,在时间方面和空间界限方面效率很高。我们表明了这些转换可以高效的执行,它让其只是随着程序大小缓慢的增加;同时将 SSA 转换中的早期步骤应用于将图反向是计算控制依赖的一种高效方法。这有力地证明了 SSA 形式和控制依赖形式是优化的实际基础。
致谢
我们想要感谢 Fran Allen,Julian Padget,和 Tom Reps 给与有帮助的评论。
引用
略。